7.14. Толщина зуба по произвольной окружности.Условие отсутствия заострения

Из рис. 7.16, б следует: _x+_x=+.Учитывая, что угол в радианах есть отношение дуги к радиусу:

,

и что =inv, _x=inv_x ( - угол зацепления), полу­чим:

Р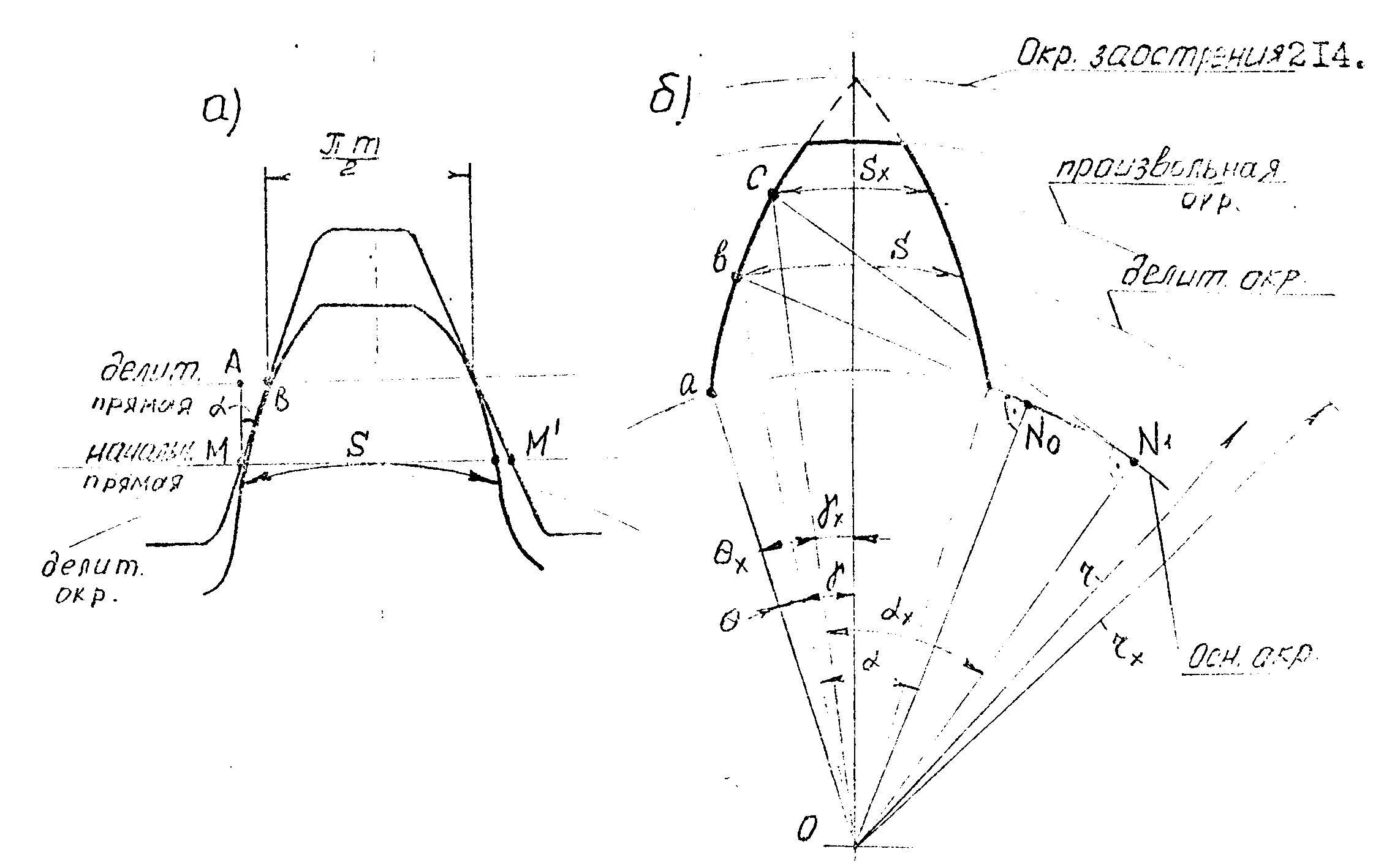 ис. 7.16. Определение толшины зуба по делительной и произвольной окружности.

Р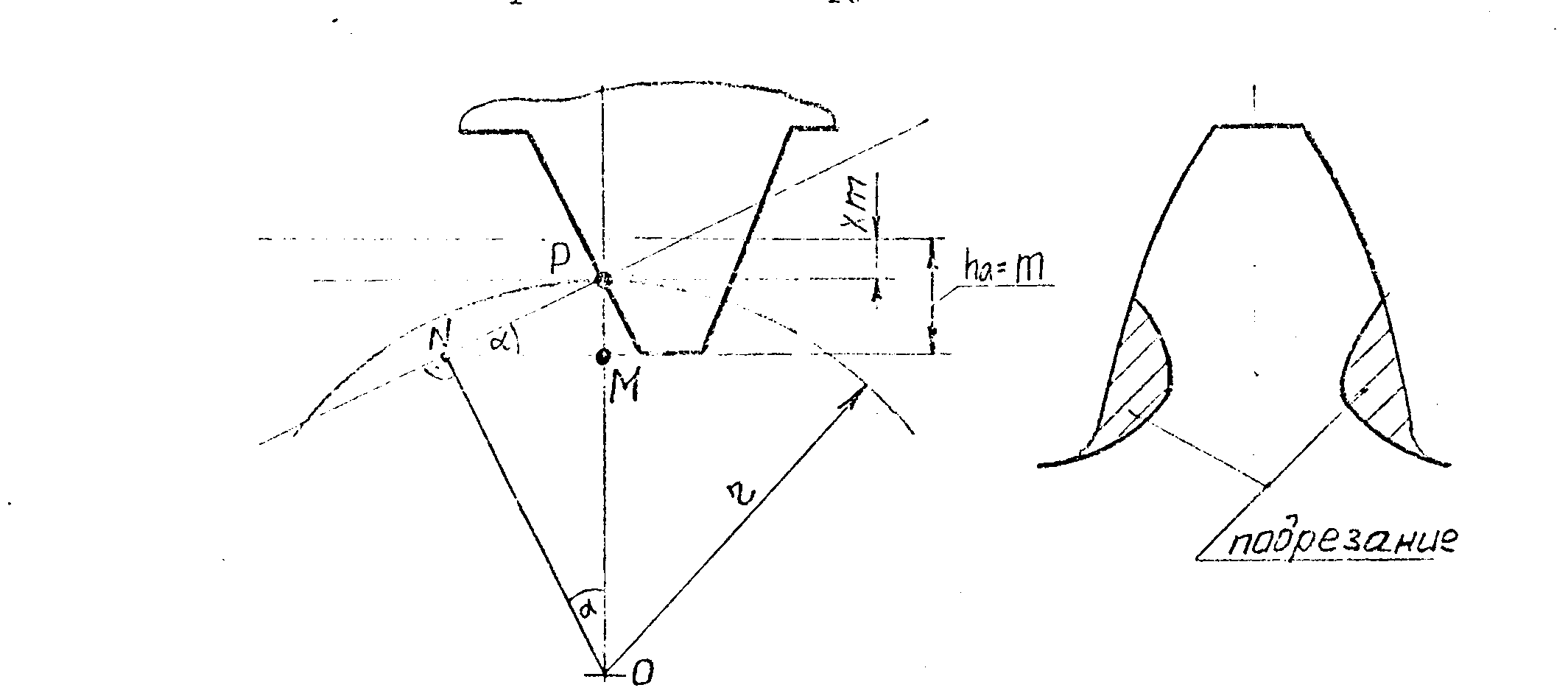 ис 7.17. Подрезание зуба.

Р ис. 7.18. К выводу основного уровнения зацепления.

.

Откуда .

Учитывая, что r=mz/2, r_x=m_xz/2,

,

получим окончательно

, (7.12)

где =20, m_x=p_x/, _x=r_b/r_x

Условие отсутствия заострения

При нарезании положительных колес с увеличением коэффициента смещения толщина зуба у вершины S_a будет уменьшаться. При не­котором x_max наступает заострение зуба, S_a =0. Эта опасность наиболее вероятна при z< 15. Во избежание излома вершины заос­тренного зуба коэффициент смещения назначают так, чтобы соблюда­лось условие S_a0,2m где

Если условие не выполняется, необходимо уменьшить x.

Зависимость между модулями по делительной и произвольной окружностям

Из основной теоремы зацепления имеем,

r_b=rcos=r_xcos_x ,

откуда

,

где r_b и r_x - радиусы основной и произвольной окружностей.

Учитывая, что r_i=m_iz/2 , получим

. (7.13)

А так как m_i=P_i/, то получим, что шаги по разным окружностям не равны между собой:

.

7.15. Условие отсутствия подрезания

При малых числах зубьев обрабатываемого колоса может наблю­даться интерференция зубьев инструмента и колеса. В этом случае режущие кромки инструмента срежут часть обрабатываемого зуба, на которую они накладываются.

Срезание части номинальной поверхности у основания зуба обрабатываемого зубчатого колеса в результате интеференции зубьев при станочном запеллеяяи называется подрезанием .

Значительное подрезание ослабляет ножку зуба и может сре­зать часть эвольвенты, поэтому оно является недопустимым,,

Явление подрезания при нарезании совиздает с явлением зак­линивания в реечной передаче. Оно происходят, когда активная ли­ния зацепления выходит за пределы линии згщепления. В реечном за­цеплении эта линия ограничена т. N (рис. 7.17.), следовательно, предельный случай, когда подрезания нет, характеризуется совпа­дением точек А и N , т.е. когда прямая точек притупления проходит через т. A (скругленный участок ИПК не учитывается, т.к. эвольвентная часть зуба образуется только прямолинейным участком). Условие отсутствия подрезания:

h_a-xmPM

Но h_a=m, а из NPM PM=PNsin.

Из PNO: PN=OPsin=mzsin/2.

Тогда

или

где x_min - наименьший коэффициент смещения, при котором от­сутствует подрезание.

При =20°

. (7.14)

Ддя устранения подрезания при числе зубьев меньше 17 необ­ходимо применять положительное смещение, определяя его величину по (7.14). При z=17 x=0, для колес с z>17 можно применять .шобое смещение. т.к. x_min<0

Лекция 30

План лекции

7.16 Эвольвентное беззазорное зацепление. Определение межосевого расстояния и угла зацепления. Восприни­маемое и уравнительное смещение.