Лекция 29. План лекции

7.11.Станочное зацепление эвольвентного колеса с реечным инструментом.

7.12 .Смещение исходного контура и его влияние на форму нарезаемых зубьев

7.13. Определение размеров колеса.

7.14. Толщина зуба по произвольной окружности.Условие отсутствия заострения.

7.15.Условия отсутствия подрезания.

7.11. Станочное зацепление эвольвентного колеса с реечным инструментом.

Рабочее зацепление – это зацепление пары колес, составляющих зубчатую передачу и непосредственно использующихся в механизме.

Производящей поверхностью называется воображаемая поверхность, образуемая режущими кромками инструмента при их движении, огибающей которой в относительном движении является требуемая боковая поверхность зуба обрабатываемого зубчатого колеса.

Станочным зацеплением называется зубчатое зацепление производющего колеса с обрабатываемым зубчатым колесом. То как бы схема взаимодействия исходного контура инструмента с нарезаемым колесом.

Исходный производящий контур (ИПК) – это проекция производящей поверхности на плоскость заготовки.

В станочном зацеплении зацепление получает те форму и размер, которые будут в рабочем зацеплении. Расчет зубчатых передач производится на базе ИПК, который определяет все размеры передачи.

Геометрические элементы ИПК стандартизованы по ГОСТ 9587-68.

Профиль зуба режущего инструмента отличается от аналогичного профиля зуба рейки тем, что высота головки увеличена на высоту радиального зазора, так как головка зуба режущего инструмента вырезает ножку зуба в заготовке.

В ИПК (рис.7.13) ав - прямолинейный участок (формирует эвольвентную часть зуба), вс- переходный. Коэффициент h  =1, с=0,25, угол инструмента =20, радиус скругления =0,38m (вводится для уменьшения подрезания зубьев и получения более плпвной переходной кривой у основания зубьев).

12. Смещение исходного контура и его влияние на форму нарезаемых зубьев.

Если делительная окружность колеса при нарезании касается делительной прямой производящей рейки, то получается колесо без смещения (нулевое) (рис.7.13).

Так как по делительной прямой толщина зуба и ширина впадины одинаковы и равны m.2, то для таких колес соблюдается равенство S=e= m./2 (колесо с равноделенным шагом).

13. Определение размеров колеса

Диаметры окружностей таких колес

d_a = mz + 2m = m(z + 2),

d_f = mz – 2,5m = m(z – 2,5),

d = mz,

d_b = mz cos.

Высота h_a = m, h_f = 1,25m, h = 2,25m.

Р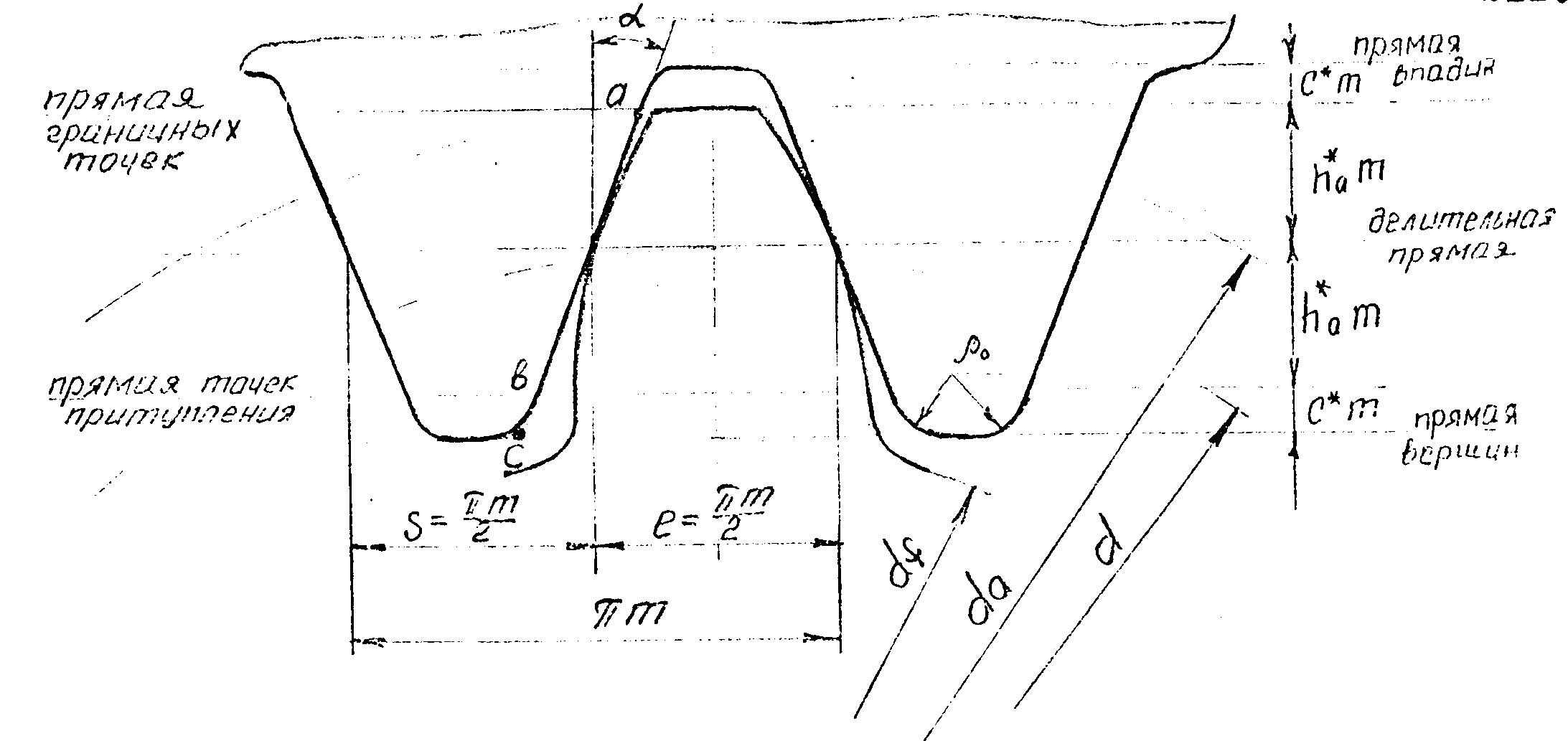 ис. 7.13. Исходный призводящий контур.

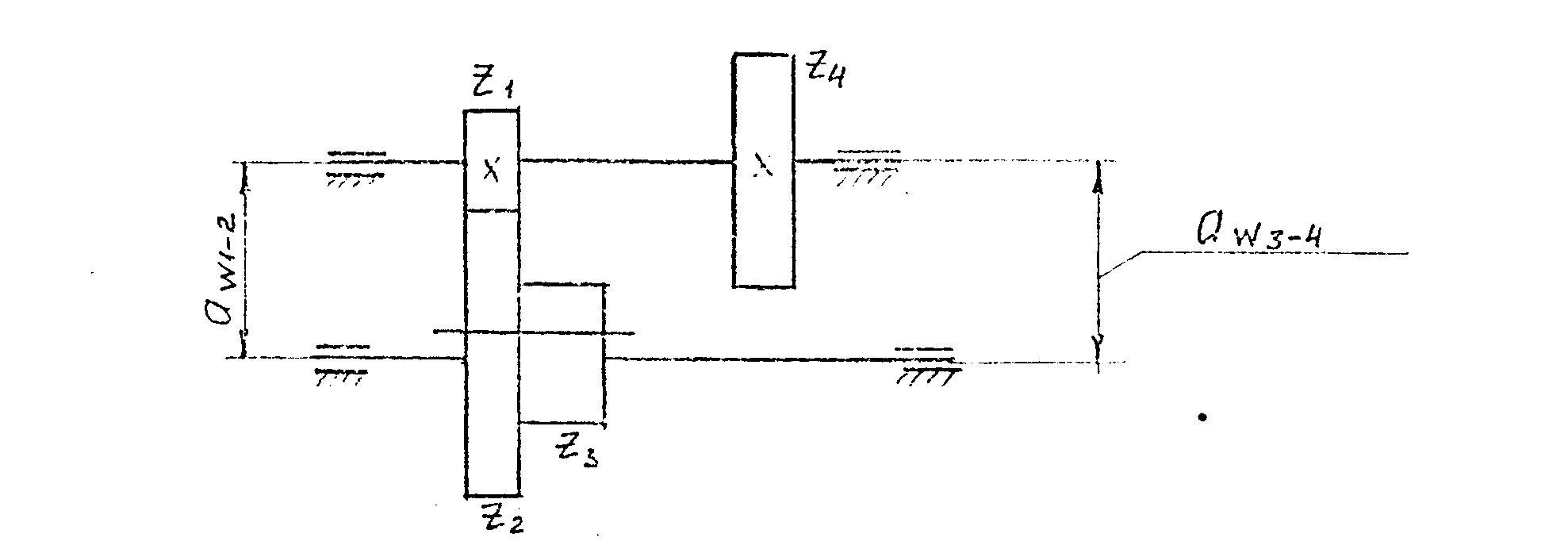
Рис. 7.14. Соосная передача.

Р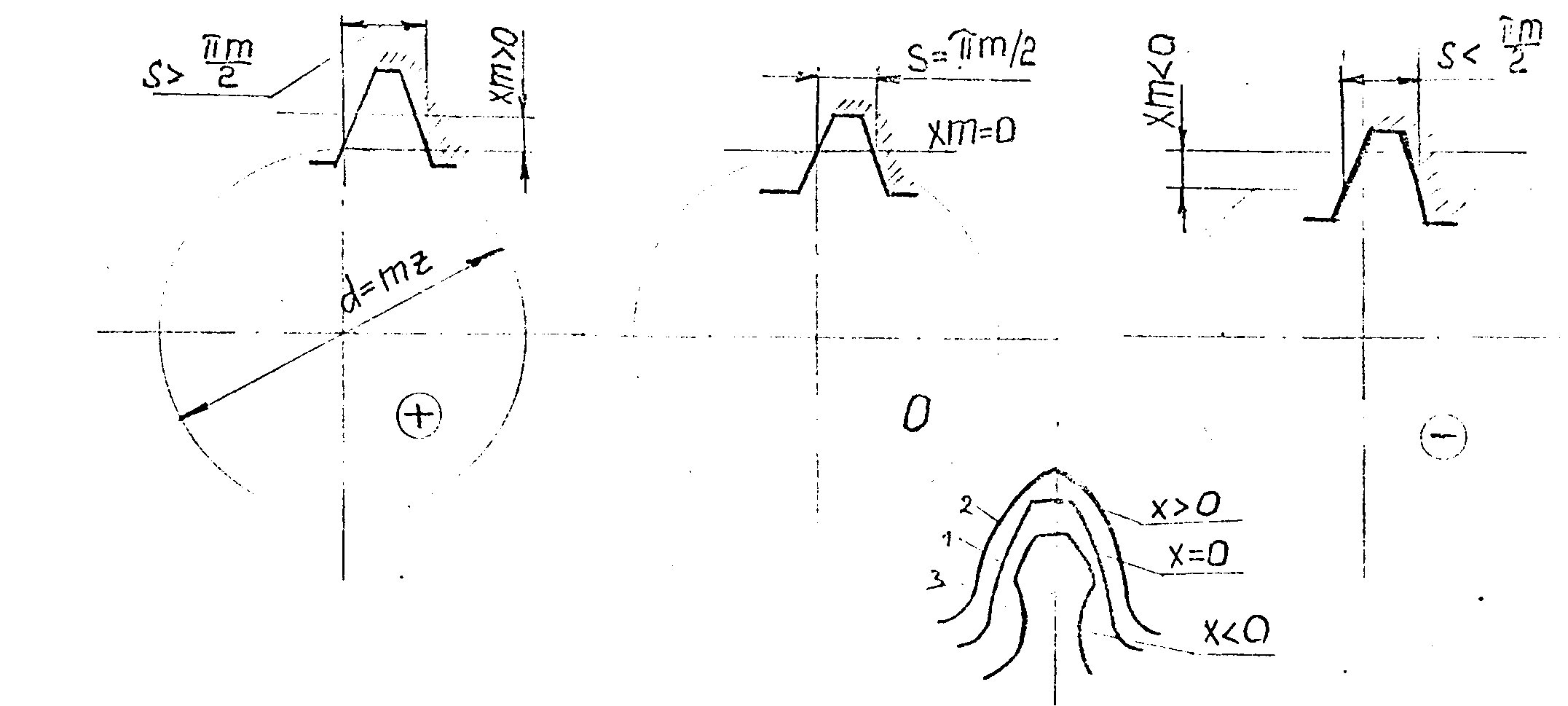 ис. 7.15. Смещение рейки и её влияние на форму зуба.

Минимальное число зубьев колес, нарезаемое без подрезания, zmin= 17.

. Нарезание колес со смещением

На станке инструмент можно расположить по-разному относительно колес. Колесо со смещением называется колесо, делительная окружность которого при нарезании не касается делительной прямой ИПК.

Применение нормальных колес с постоянной высотой головки зубьев вызвано требованиями взаимозаменяемости. Но использование таких колес ограничивает конструктора в выборе наилучших для работы передачи параметров. Причинами изготовления колес со смещениями являются следующие.

1. Снижение числа зубьев может привести может привести к подрезанию ножки (при t  17).

2. Часто невозможно применить нормальную зубчатую передачу у соосных передач. Например (рис. 7.14): расстояние а₁₂ должно равняться а₃₁. Но при одинаковом модуле и нулевых колёсах это невозможно:

3. Нормальное зацепление может не удовлетворять конструктора по качественным показателям: коэффициенту перекрытия, удельному скольжению, давлению, форме зуба и т.д.

Во всех случаях, когда нормальное зубчатое зацепление не удовлетворяет предъявляемым требованиям, от него приходитеся: от­ступать или исправлять его. Исправление нормального зубчатого зацепления с целью его улучшения называется корригированием.Осуществляется оно нарезанием колес со смещением,,

Так как шаг по всем сечениям рейки одинаков, то число зубь­ев колеса и шаг по делительной окружности при смещении не меняет­ся (так же, как и передаточное отношение и эвольвента, т.к. не меняется основная окружность). Разница будет в толщине зуба и ши­рине впадины, а также в диаметрах окружностей вершин и впадин.

Смещение и его влияние на форму зуба

Смещением называется расстояние по нормали между делительной окружностью зубчатого колеса и делительной прямой производящей рейки.

Его выражают в виде произведения модуля m на коэсяоициент смещения x. Смещение имеет знак (рис.7.15). При положитель­ном смещении (х>0) делительная прямая рейки не пересекает де­лительной окружности колеса (рейка смещена от центра заготовки). При нулевом делительная прямая касается делительной окружности (x=0). При отрицательном прямая пересекает делительную ок­ружность (рейка смещена к центру заготовки, Х < 0).

Смещение влияет на форму зуба (см.рис.). Первый профиль со­ответствует колесу без смещения, Второй - колесу с поло­жительным смещением. Основание зуба - утолщенное, , но мо­жет быть заострение головки. Третий профиль соответствует колесу с отрицательным смещением. Ножка ослаблена, .

. Толщина зуба по делительной окружности

Так как колесо нарезается со смещением, то по делительной окружности перекатывается некоторая начальная прямая (рис.7,16,а). Она перекатывается без скольжения, поэтому толщина зуба по дели­тельной окружности равна ширине впадины по начальной прямой:

(7.11)