Лекция 20.
План лекции.
4.6. Синтез механизмов методом наилучшего приближения функций.
4.7. Метод квадратичного приближения.
4.6. Синтез механизмов методом наилучшего приближения функций.
Для того, чтобы функция F(z) наименее отклонялась от j(z) необходимо, чтобы максимальные абсолютные значения отклонения DB(z)max или D(z)max были минимальными. Этому условию приближения интерполяционный метод не удовлетворяет.
Основоположником теории наилучшего приближения функций П. Л. Чебышевым доказана теорема о том, что существует такая система параметров Р0, Р1…Р, для которой максимальные отклонения будут минимальными по абсолютной величине, и достигают они этих предельных значений не менее (n+2) раза, последовательно меняя свой знак ( рис. 4.5). Обозначим DB(z)max=e l, e=±1,L - предельное значение взвешенного отклонения функции. Понятно, что в экстремальных точках первые производные отклонений будут равны нулю.
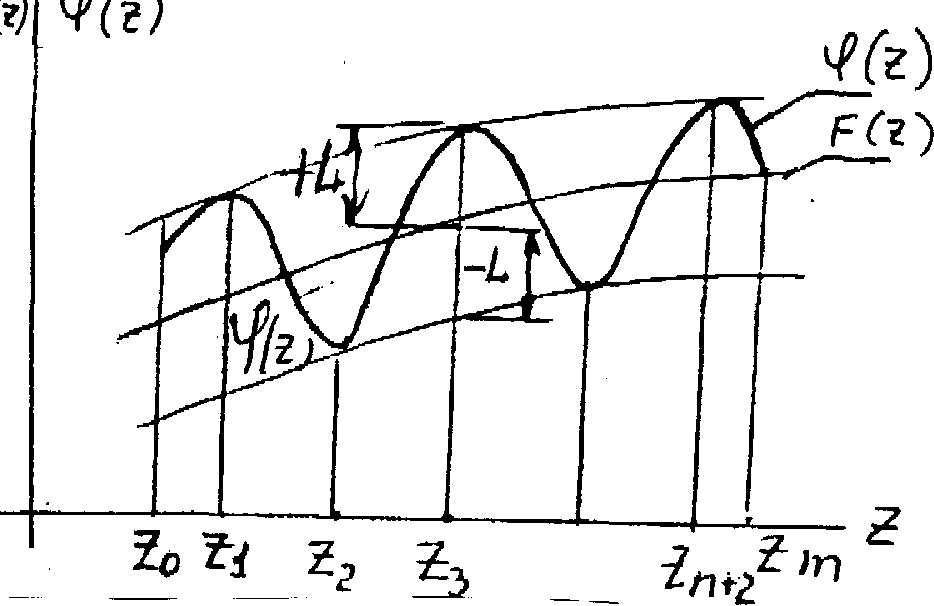
Рис. 4.5 К методу наилучшего приближения функций.
На основании сказанного можно составить системы уравнений:
DB=(z1)=el DB=(z2)=-el DB=(zn+2)=(-1)n-1el (4.8)
производные:
D’B(z1)=0 D’B(z2)=0 D’B(zn+2)=0 (49)
Таким образом, общее число уравнений (8) и (9) равно 2(n+2), а неизвестных: n+1-значений Рo,P1…Рn); n+2 -значений Z, в которых взвешенное отклонение достигает предельных значений и, наконец, величина предельного отклонения L
Возможно, что на концах рассматриваемого интервала отклонение также достигает своего максимального значения. Тогда, поскольку Z0 и Zm заданы, число неизвестных уменьшается на 2 и, так как на концах интервала производные могут быть не равны нулю, то из (9) исключаются два уравнения. В таком случае (8) и (9) принимают вид:
DB(z0)=el DB(z1)=-el DB(zn)=(-1)nel DB(zm)=(-1)n+1el (4.81)
В примера рассмотрим кулисный механизм (рис. 4.6). Определим l1,l2,l3 и расстояние до прямой x=l, которую приближенно, но с наименьшим отклонением воспроизводит точка Д, при повороте кривошипа на некоторый угол a. Обозначим через d - предельное отклонение D(z) Предельное взвешенное отклонение DB(z) будет-L=d/A
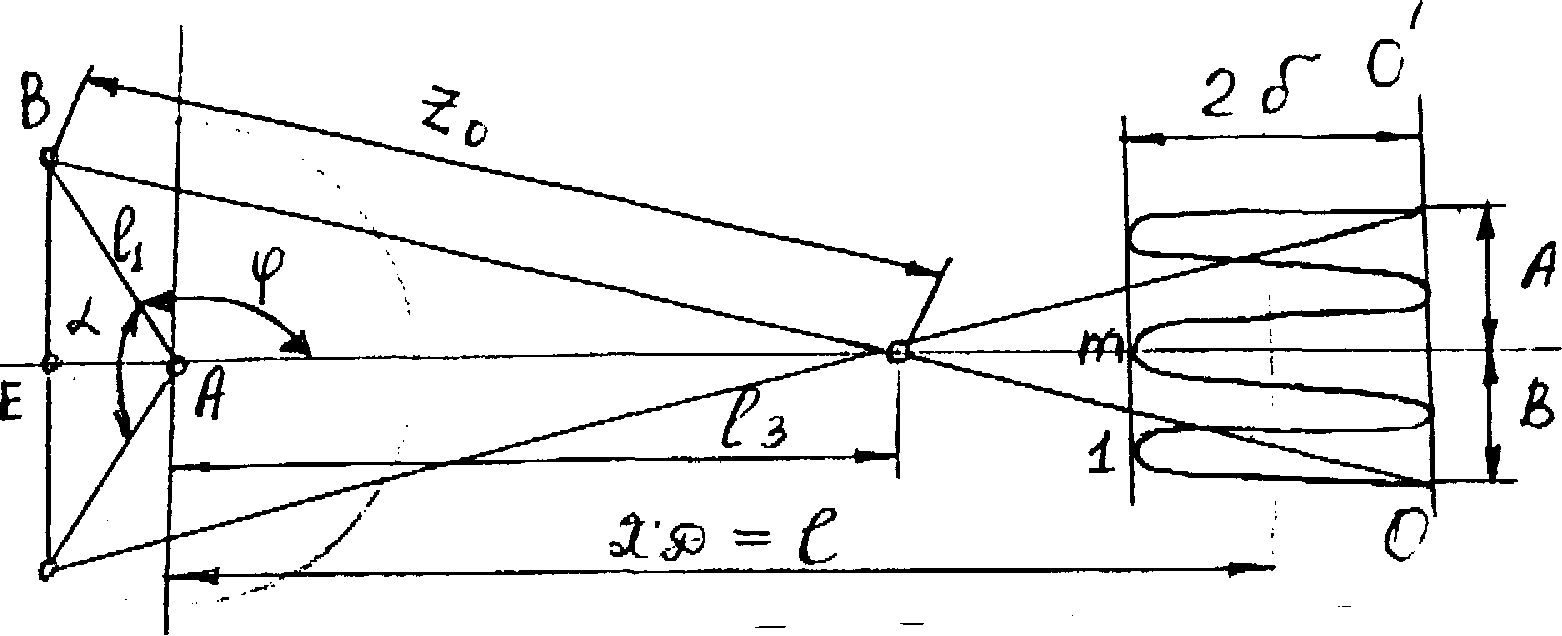
Рис. 4.6 К методу наилучшего приближения функций*
Будем считать, что d достигает экстремальных значений и на краях заданного интервала.
Тогда будем иметь 4 точки (так полином (5) второго порядка, в которых взвешенная разность DB достигает своей максимальной величины. Таким образом, получаем системы уравнений:
DB(z0)=P0+P1z0+P21/z0+z02=d/A
DB(z1)=P0+P1z1+P21/z1+z12= -d/A
DB(z2)=P0+P1z2+P21/z2+z22=d/A
DB(zm)=P0+P1zm+P21/zm+zm2= -d/A (4.10)
D’B(z1)=P1-P21/z12+2z1=0
D’B(z2)=P1-P21/z22+z2=0
На основании (5) и (10) получим уравнения:
l2=2z1+zm=z0+2zm
2l3l-l32-l12+2l3d=2z0z2+z22 (4.11)
l2(l32-l12)=z12zm=z0z22
В (II) шесть неизвестных: .l1, l2, l3, l, z1, z2.
Для определения необходимо еще 2 уравнения. Так как данный механизм симметричный, то точка Д при повороте кривошипа на угол приближенно воспроизводит 2 участка прямой линии, расположенных по обе стороны от оси Х (А и В). Следовательно, значение параметра Z0 будет соответствовать двум крайним положениям точки Д (Д0 и Д01), а Zm среднему положению -Дт, когда шатун и кривошип сливаются в одну линию.
Zm=l1+l2 (4. 12)
Наконец, рассматривая треугольники СВЕ и ABE, найдем
(l3+l1sina/2)2=l32 (4.13)
Решая совместно уравнения (4.12), (4.13), (4.11) отделим все необходимые размеры механизма, удовлетворяющие поставленному выше условию.
Рассмотренные выше приближенные методы являются наиболее универсальными: они имеют применение не только для геометрического синтеза, но и для решения множества других задач, связанных, например, с проектированием механизмов с заранее заданными динамическими и кинематическими свойствами. Известно, например, задача по приближенному синтезу рычажных механизмов с минимальным отклонением угловой скорости начального звена (кривошипа) от некоторого наперед заданного постоянного значения, по проектированию минимальной массы маховика, удовлетворяющей заданному коэффициенту неравномерности хода машины и ряд других.