3.8.13 Определение момента инерции маховика.

Для решения второй и третьей задач, по формулам при­ведения расчитаем значения приведенного момента инерции во всех положениях механизма и построим график J_пр=f().

Складывая соответствующие ординаты графиков A_g=f() и A_c=f() построим график избыточных работ E=f() по формуле

E_i=A_gi+A_ci

где A_gi,A_ci - работа движущих сил и сил сопротивления в i- положении.

Графически исключая параметр  из графиков E=f() и J_пр=f() построим диаграмму E=f(J_пр) называемую диа­граммой "энергия-масса" или диаграмма Виттенбауэра (рис.4.42)

Для установившегося движения диаграмма Виттенбауэра является замкнутой кривой, для переходных режимов - разом­кнутой.

О пределим координаты точки i на диаграмме E=f(J_пр)[E_i;J_прi].

Допусим известна начальная кинематическая энергия ме­ханизма К₀.

Т огда полное значение кинетической энергии для этого положения

k_i=k₀+_i, т.к. k_i=_Ak_i, k₀=_Ak₀, E_i=_AE_i

( где _А - масштабный коэффициент графика работ _А=_M_H) получим:

k_i=k₀+E_i

В еличину k₀- отложим вниз от оси абсцисс.

Для обеспечения заданного при проектировании коэффи­циента неравномерности  в механизм введем маховик с моментом инерции J_M , установив его на ведущем звене.

Тогда суммарный момент инерции механизма увеличится на JM.

J_i=J_M+J_прi

Разделив все члены этого равенства на _J получим:

J _i=J_M+J_прi

Значение J_M отложим влево от оси ординат. По концам отрез­ков К₀ и J_M построим новую систему координат.

Соединив прямой линией точку i с началом новой сис­темы координат, найдем угол, который образует эта прямая с осью абсцисс (угол _i).

Из рис. 3.42 (3.63)

Кинетическая энергия механизма с моментом инерции J_i

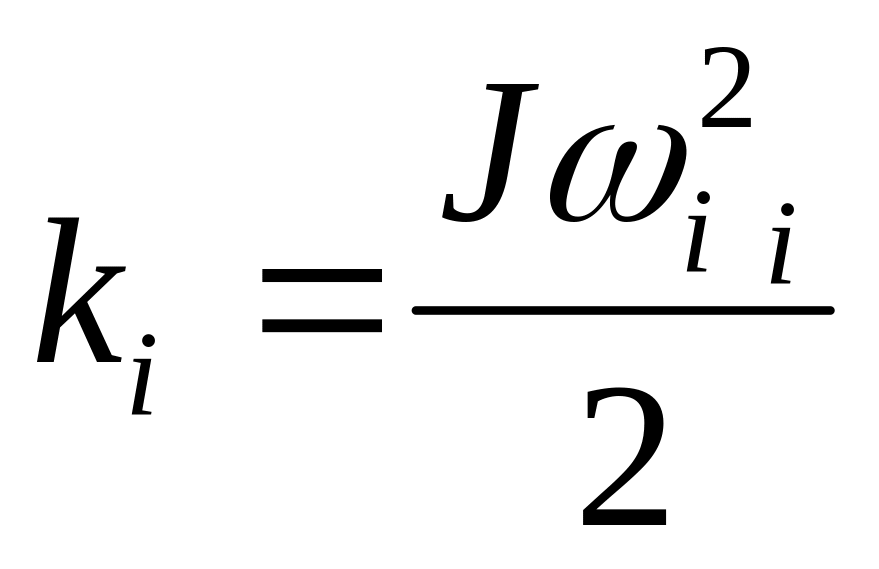(3.64)

Преобразуя выражение (3.64)

(3.65)

откуда (3.66)

или (3.67)

Экстремальные значения _i(_max,_min) и позволяют опре­делить начало координат новой системы.

Из условия, что и

Находим и

Пусть по формуле (3.46) вручную или на компьютере вычислены значения M_пр=f₁(), M_прg=f₂() известен по параметрам двигателя и редуктора. (M_прg - приведенный момент движущих сил).

Лекция 18.

План лекции.

3.8.15 Установившееся движение машины с учетом упругости звеньев. Определение жесткости приводного устройства.

3.8.16 Уравнение движения машины с учетом упругости звеньев.

3.9. Виброзащита машин.

3.8.15 Установившееся движение машины с учетом упругости звеньев. Определение жесткости приводного устройства.

Ранее предполагалось, что все звенья механизмов явля­ются абсолютно жесткими. В действительности, каждое из звеньев является упругим; при передачи усилий оно деформи­руется. Деформация звеньев приводит к дополни те льным дина­мическим нагрузкам и ошибкам.

Рассмотрим влияние на динамику машины упругости. Наи­более важной характеристикой привода, отражающей это влия­ние, является его жесткость. Покажем, каким образом может быть определена жесткость привода на примере цилиндричес­кого редуктора. Здесь 0 - двигатель, 1,2,3,4 - зубчатые колеса, 5 - ведомое звено (рис.3.44). С₀₁, С₁₂, …С₄₅ - жесткости валов и зубчатых передач. Под жесткостью вала понимается его жесткость на кручение.

где G - модуль упругости второго рода;

Jp - полярный момент инерции сечения;

l - длина вала.

Жесткость цилиндрических зубчатых колес определяется формулой: c=kR²b

где R - радиус начальной окружности ведущего колеса;

b - ширина зубчатого венца в СМ;

k - коэффициент, принимаемый для стальных колес, равным К=15*10⁵ н/см2

Пусть к выходному звену (валу) механизма приложен мо­мент М, а ведомое звено 5 остается неподвижным. При этом из-за податливости всех промежуточных элементов входной вал повернется на некоторый угол . Отношение С = N/ называется жесткостью передаточного механизма. Последо­вательно определяя угловые деформации каждого из упругих элементов механизма и привода эти деформации к входному валу, подучим

(3.72)

где

u₁₂=z₂/z₁; u₁₄=z₂z₄/z₁z₃,

z_i - число зубьев i -го колеса

тогда 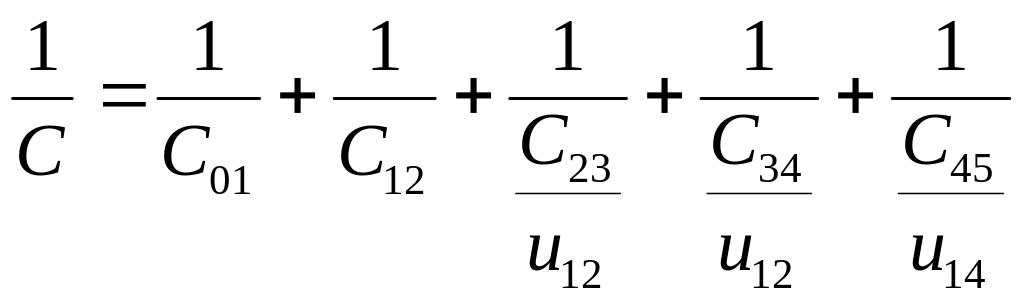(3.73)

Отсюда видно, что при последовательном соединении складываются величины, обратные жесткости, называемые податливостями элементов.

При параллельном соединении механизмов

С=С_iпр (3.74)

Пользуясь формулами (3.73) и (3.72) можно определить жесткость разветвленных кинематических цепей. При опреде­лении жесткости часто также учитывают жесткости шпоночных, шлицевых соединений и т.п. Формулы для их определения при­водятся, например, в книге И.И. Вудьфсона "Динамические рас­четы цикловых механизмов" П.Машиностроение,1976г.