Разрешим уравнение (3.57) относительно углового ускорения

(3.58)

Рассмотрим случай, когда

1. Пусть и , тогда ,

Для рычажных механизмов описываются разными функциями, поэтому равенства между ними быть не может.

Но существуют машины, где это равенство выполняется за счет регуляторов скорости.

2.Пусть Этому случаю отвечают ротационные машины (турбины и т.д.) Для рычажных механизмов этот случай невозможен, т.к. у них

Уменьшение колебания угловой скорости может быть достигнуто за счет увеличения приведенного момента инерции (см.(3.58)). Это достигается за счет введения в машину добавочной массы в виде диска - маховика.

3.8.10 Решение уравнений движения машины аналитическим методом.

Решение уравнений движения машины производят с целью определения кинематических параметров (перемещений, ) с учетом действующих сил и масс.

При решении ставятся и другие задачи - определение неравномерности хода и т.д.

Уравнения движения устанавливают связь между 3 типами параметров: 1) силовыми

2) инерционными

3) кинематическими

Если внешние силы являются функциями положения, то можно решение уравнений записать в форме интеграла энергии.

Решение уравнений движения в форме интеграла энергии.

Перепишем еще раз уравнение движения в форме интеграла энергии

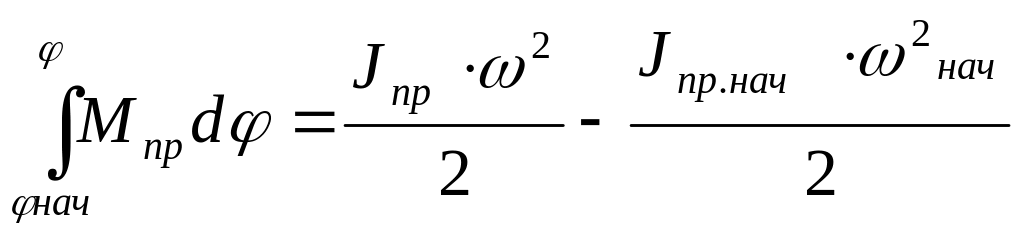
Разрешая её относительно 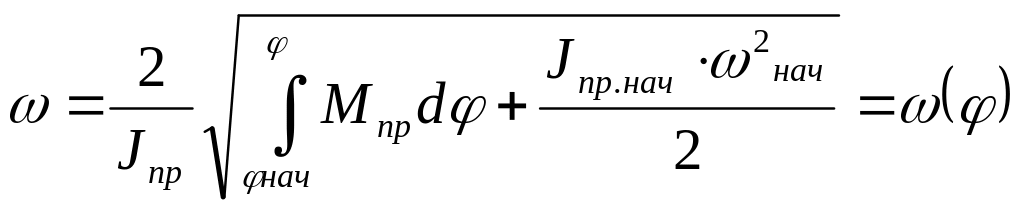(3.59)

Величина будет зависеть от ,т.е. от обобщенной координаты.

Для решения (3.59) необходимо знать начальную кинетическую энергию

; откуда (3.60)

Если из уравнений (3.59) и (3.60) исключить параметр , то получим: (3.61)

, или

Интегрирование выражений (3.60) и (3.61) возможно только численным методом.

3.8.11. Неравномерность движения машины при установившемся режиме. Назначение маховика.

Как уже было сказано, ведущее звено вращается неравномерно. Причинами колебания скорости является:

- периодическое изменение внешних сил

- периодическое изменение момента инерции

Периоды этих функций либо одинаковы, либо кратны, поэтому колебания скорости носят периодический характер. Периодические колебания скорости ведущего звена называются неравномерностью хода машины.

Их оценивает коэффициент неравномерности.

Найдем

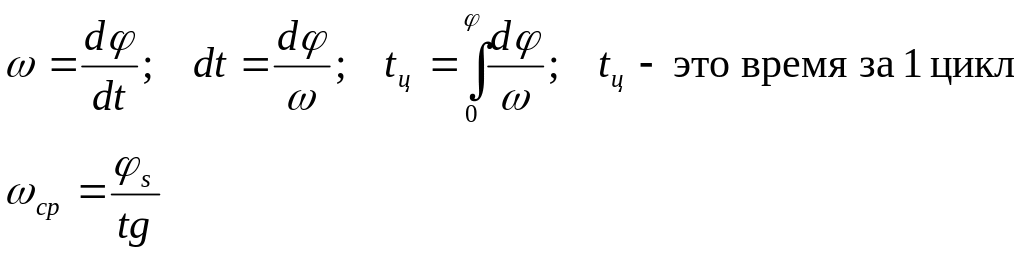
Цикл - это время через которое повторяются значения .

На практике:

Неравномерность хода машин приводит к дополнительным динамическим нагрузкам, поэтому при проектировании машин стараются уменьшить его.

Достигается это: рациональным распределением масс в звеньях, применением регуляторов скорости, но проще всего это достигается с помощью маховика.

Маховик - это массивное тело в виде диска, обладающего большой инерцией. Он является аккумулятором кинетической энергии.

При увеличении скорости машины, увеличивается скорость маховика, увеличивается его кинетическая энергия, на что затрачивается часть энергии движущих сил и темп роста скорости машины уменьшается. При уменьшении скорости машины уменьшается скорость маховика, высвобождается часть его кинетической энергии, которая добавляется к энергии движущих сил и темп замедления уменьшается.

Таким образом, маховик сглаживает колебания. Маховик выгоднее устанавливать на быстроходных валах, т.к. нужный эффект по сглаживанию получают с помощью маховика меньшей массы.

Лекция 17.

План лекции.

3.8.12 Решение уравнения движения графоанали­тическим методом Виттенбауэра.

3.8.13 Определение момента инерции маховика.

3.8.14 Алгоритм определения закона движения машины и момента инерции маховика на ЭВМ.

3.8.12 Решение уравнения движения графоанали­тическим методом Виттенбауэра.

Этот метод позволяет решить три задачи:

1. Определить необходимый момент движущих сил М_g для подбора двигателя и расчёта редуктора, приводящего в движение механизм.

2. Подобрать маховик (расчитать J маховика) для обеспечения заданного при проектировании коэффициента неравномерности движения .

3. Установить истинный закон движения механизма =f()

Решение всех трех задач базируется на законе сохра­нения энергии.

Рассмотрим случай, когда известны все внешние силы, включающие: силы сопротивления и силы тяжести. Требуется определить момент движущих сил.

По формулам приведения вычисляются значения приведен­ного момента сил в различных положениях механизма и строит­ся график M_пр = f(). Путем графического интегрирования из графика M_пр = f() получают график работ сил сопротивления в пределах одного цикла движения механизма (рис.3.42).

Для установившегося движения сумма всех работ за цикл равна нулю.

A=0

Так как работа сил тяжести за цикл будет равна нулю, то равенство будет выполняться, если работа движущих сил за цикл будет равна работе сил сопротивления за цикл по абсолютной величине.

A_g_ц=А_с_ц (3.62)

Уравнение (3.62) является основным энергетическим уравне­нием установившегося режима.

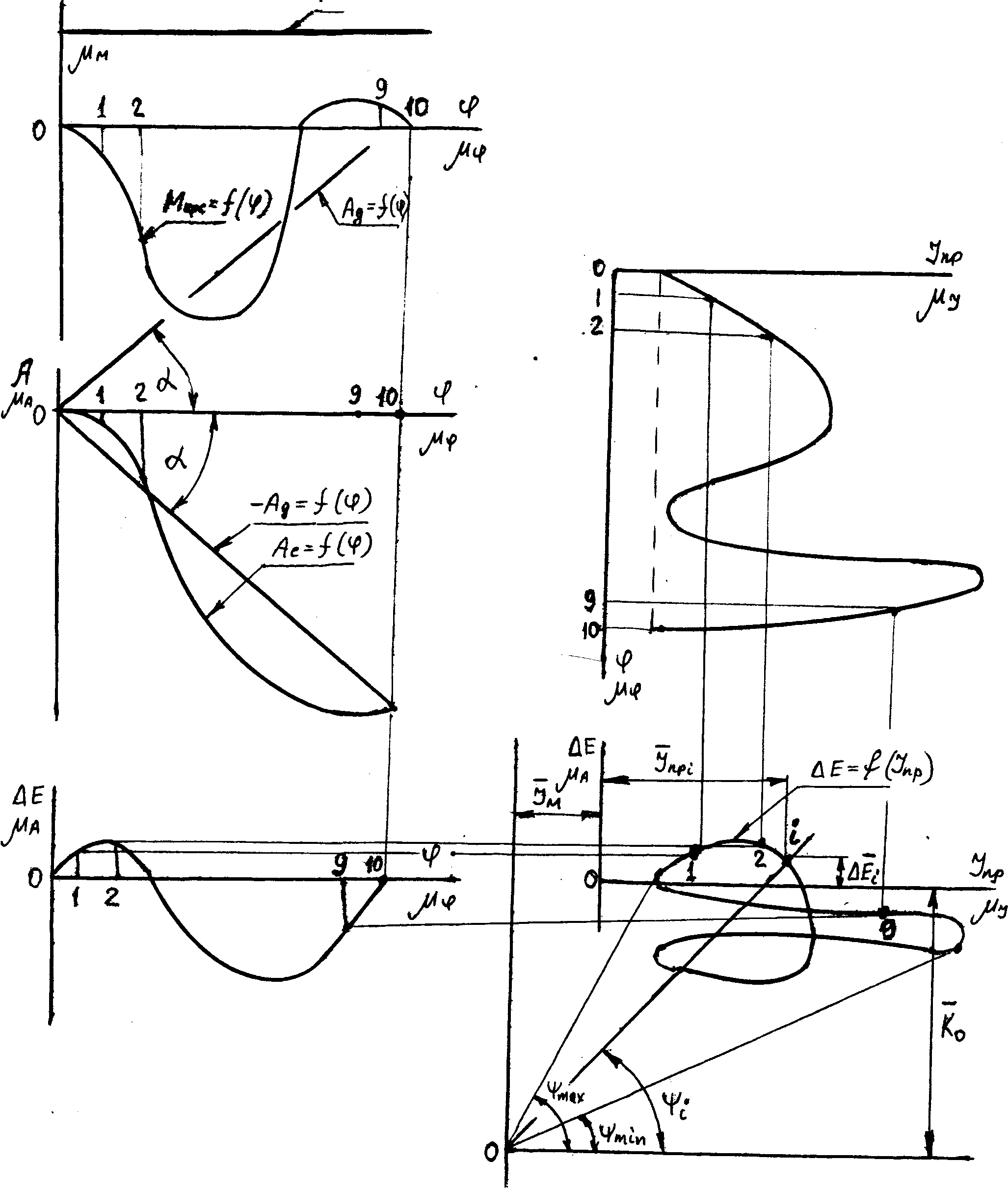
Рис 3.42 Графоаналитический метод решения уравнения движения машины,

где

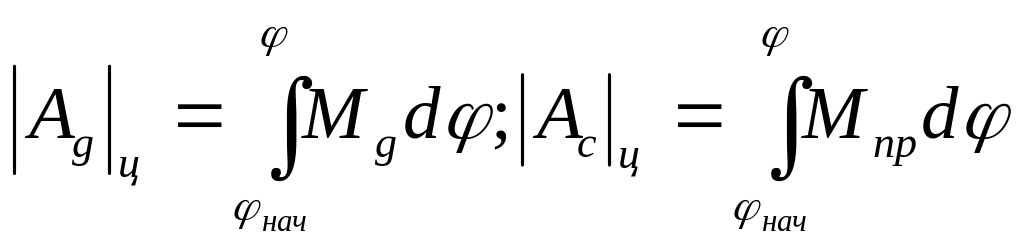
Если цикл движения соответствует обороту ведущего звена, момент движущих сил является постоянной величи­ной, то:

А_g_ц=М_g2

Для установившегося движения работа сил сопротивле­ния и работа движущих сил в начале и конце цикла должны быть равны, при необязательном равенстве внутри цикла.

А при учете того, что М_g=const, график симметричный относительно оси абсцисс графику работ сил движущих, представляет собой прямую, соединяющую начало и конец графика А_c.

Построив график A_g=f() и графически продифференциро­вав его, получим график момента движущих сил, необходимый для подбора двигателя и расчета редуктора.