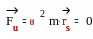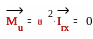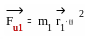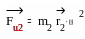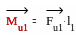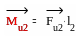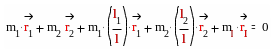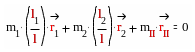- •Кафедра «Теория механизмов и машин» теория механизмов и машин конспект лекций
- •Лекция 31. Пространственные зубчатые передачи.
- •1.2. Механизмы современной техники.
- •1.3. Задачи и основные методы теории механизмов и машин.
- •План лекции
- •1. 5. 2 Классификация кинематических пар по числу связей.
- •1.5.3 Степень подвижности кинематической цепи.
- •5. 7 Избыточные связи.
- •План лекции
- •1. 5. 5 Образование механизма из кинематической цепи.
- •1. 5. 6 Принцип образования механизмов по Ассуру.
- •1. 5. 6 Принцип образования механизмов по Ассуру.
- •1. 5. 7 Избыточные связи
- •1. 5. 8 Классификация механизмов по общим свойствам.
- •1.5.9 Виды механизмов.
- •Тема 2
- •Лекция 4 План лекции
- •2. 2 Графический метод кинематического анализа - метод кинематических диаграмм.
- •2. 2. 1 Определение положений звеньев, построение траекторий точек и кинематических диаграмм.
- •2. 2. 2 Графическое дифференцирование.
- •2.2.3 Графическое интегрирование.
- •2.3.1 Построение планов скоростей.
- •2.3.2 Построение планов ускорений.
- •2.5 Метод преобразования координат.
- •2.5.1. Определение положений точек в незамкнутых кинематических цепях.
- •2.5.2 Определение положений точек в замкнутых кинематических цепях.
- •2. 14 Преобразование координатных систем.
- •2 .5.4 Уравнения преобразования координат для конкретных кинематических пар,
- •5. 5 Определение положения захвата пространственного манипулятора в неподвижной системе координат.
- •Лекция 8
- •2.5.6 Определение положения точек в плоских механизмах
- •2.5.7 Определение положений точек, скоростей и ускорений
- •2.5.6 Определение положений точек в плоских механизмах векторным методом.
- •2.5.7 Определение угловых скоростей и ускорений звеньев и линейных скоростей и ускорений точек плоских механизмов. Аналоги скоростей и ускорений.
- •3.1. Введение в динамику машин.
- •3.2.1 Классификация сил.
- •3.1 Введение в динамику машин.
- •3.2. Силы, действующие в машинах.
- •3.2.1 Классификация сил.
- •Внешние и внутренние силы.
- •2. Силы движущие и силы сопротивления.
- •3.2.2 Определение сил инерции.
- •3.4.Кинетостатический расчет механизмов.
- •3.4.1 Задачи кинетостатики механизмов.
- •3.4.2 Условия статической определимости групп звеньев.
- •3.4.3 Графоаналитический метод кинетостатического расчета групп второго класса.
- •2. Группа 2-го вида
- •3.4.4 Аналитический метод кинетостатического
- •3.4.5 Кинетостатика ведущего звена.
- •3.4.4 Аналитический метод кинетостатического
- •Лекция 12. План лекции.
- •3.5.1 Трение в поступательных кинематических
- •3.5.2 Трение во вращательной кинематической паре.
- •3. 6. Передача работы и мощности. Кпд машин. Коэффициент потерь.
- •3.6.1 Кпд поступательной кинематической пары.
- •3.6.3. Определение кпд механизма.
- •3.6.4 Кпд соединенных машин.
- •3.7.1 Общие условия уравновешивание вращающихся масс.
- •3.7.2 Статическое уравновешивание.
- •Уравновешивание в общем случае или динамическое уравновешивание.
- •3.7.4 Статическая и динамическая балансировка вращающихся масс.
- •3.7.6. Уравновешивание шарнирного четырехзвенника.
- •3.8. Движение машин под действием заданных сил.
- •3.8.1. Режимы движения машины.
- •3.8.2. Характеристика внешних сил.
- •Кинетическая энергия звеньев и работа сил, действующих в машинах.
- •Приведение сил и масс .Динамические модели машины.
- •Определение приведенных моментов инерции и моментов сил кривошипно-ползунного механизма.
- •Приведение сил и масс. Динамические модели машины.
- •3.8.5 Определение приведенных моментов инерции и моментов сил кривошипно – ползунного механизма.
- •Лекция 16.
- •3.8.7. Уравнения движения машины в форме интеграла энергии.
- •3.8.8 Уравнения движения в дифференциальной форме.
- •Разрешим уравнение (3.57) относительно углового ускорения
- •3.8.13 Определение момента инерции маховика.
- •3.8.16 Уравнения движения машины с учетом упругости звеньев.
- •Тема 4. Общие методы синтеза механизмов. (4 часа).
- •План лекции
- •4. 1. Основные задачи и метода синтеза.
- •4. 2. Основные и дополнительные условия синтеза. Ограничения при синтезе.
- •4. 3. Методы оптимального синтеза.
- •4. 4. Синтез механизмов на основании заданной целевой функции.
- •4. 5. Интерполяционный метод синтеза механизмов.
- •Лекция 20.
- •4.6. Синтез механизмов методом наилучшего приближения функций.
- •4.7. Метод квадратичного приближения.
- •4.6. Синтез механизмов методом наилучшего приближения функций.
- •4.7. Метод квадратичного приближения.
- •Тема 5 Синтез плоских рычажных механизмов (4 часа) Лекция 21 План лекции
- •5.1 Основные условия и ограничения при синтезе.
- •5.2 Синтез четырехзвенного кривошипно-коромыслового. Механизма по трем положениям, аналитическим методом.
- •5.3 Синтез четырехзвенного кривошипно-коромыслового механизма по двум крайним положениям коромысла, коэффициенту изменения средней скорости и допускаемому углу давления.
- •5.1 Основные условия и ограничения при синтезе.
- •5.2 Синтез четырехзвенного кривошипно-ползунного коромыслового механизма по трем положениям аналитическим методом.
- •5.3 Синтез четырехзвенного кривошипно-коромыслового механизма по двум крайним положениям коромысла, коэффициенту изменения средней скорости и допускаемому углу давления.
- •План лекции
- •5.4.L Синтез кривошипно-коромыслового механизма.
- •5.4.2 Синтез кривошипно-ползунного механизма.
- •5.4.З Синтез кулисного механизма.
- •9.2. Фазы движения толкателя
- •9.3. Обоснование выбора закона движения
- •Лекция 24. План лекции.
- •6.4. Кинематический анализ кулачковых механизмов.
- •6.5 Синтез кулачковых механизмов.
- •6.6 Проектирование по кинематическим параметрам. Построение профиля кулачка при поступательном движении толкателя.
- •6.4 Проектирование по динамическим параметрам. Определение текущих углов давления. Аналог скорости
- •Лекция 25 План лекции.
- •6.10. Графическое определение текущих углов давления.
- •6.11 Аналитический метод определения основных размеров кулачкового механизма по заданному допускаемое углу давления.
- •6.12. Силовой расчет кулачкового механизма.
- •Глава 7. Синтез зубчатых зацеплений. (12 часов).
- •7.2. Основная теорема зацепления. Полюс зацепления. Центроиды колес.
- •7.3. Цилиндрическая эвольвентная зубчатая передача..
- •7.1 Виды зубчатых механизмов
- •7.2. Основная теорема зацепления. Полюс зацепления. Центроиды колес.
- •7.3. Цилиндрическая эвольвентная зубчатая передача.
- •Окружность
- •Окружность
- •5. Эвольвента - кривая без перегибо Лекция 27. План лекции
- •7.4. Элементы эвольвентного зубчатого колеса
- •Элементы и свойства эвольвентного зацепления
- •7.6 Коэффициент перекрытия
- •7.4. Элементы эвольвентного зубчатого колеса
- •7.5 Элементы и свойства эвольвентного зацепления
- •7.6. Коэффициент перекрытия
- •Лекция 28. План лекции
- •7.7. Интерференция зубьев. Условие отсутствия заклинивания
- •7.8. Внутреннее зацепление (рис.7.9)
- •7.9. Реечное зацепление (рис.7.10)
- •7.10. Изготовление зубчатых колес.
- •Лекция 29. План лекции
- •Смещение исходного контура и его влияние на форму нарезаемых зубьев.
- •Определение размеров колеса
- •7.14. Толщина зуба по произвольной окружности.Условие отсутствия заострения
- •7.15. Условие отсутствия подрезания
- •7.16 Эвольвентное беззазорное зацепление. Определение межосевого расстояния и угла зацепления. Воспринимаемое и уравнительное смещение.
- •7.17 Проектирование зубчатых передач. Выбор коэффициента смещения.
- •7.18 Косозубая цилиндрическая передача,
- •7.17 Проектирование зубчатых передач. Выбор коэффициента смещения.
- •7.18 Косозубая цилиндрическая передача.
- •7.21 Передачи с перекрещивающимися осями.
- •7.21.1 Винтовая передача.
- •7.21.2 Червячная передача.
- •Тема 8. Синтез механизмов с подвижными осями. Лекция 32.
- •Кинематическое исследование планетарных механизмов графическим методом Куцбаха – Смирнова.
- •Тема 9. Основы теории машин - автоматов. ( 4 часа)
- •План лекции:
- •9.1.2. Управление от копиров.
- •9.1.3. Следящий привод.
- •Промышленные роботы
- •9.3. Рабочий объем манипулятора и классификация движений захвата
- •9.4. Влияние расположения кинематических пар манипулятора на его маневренность
- •9.5 Структурный синтез манипуляторов
- •9.6 Зоны обслуживания, угол и коэффициент
- •Список литературы.
Уравновешивание в общем случае или динамическое уравновешивание.
Динамическому уравновешиванию подвергают детали сложной конфигурации, большой длины и с большой угловой о скоростью вращения.
.Пусть задано вращающееся тело большой длины с распределением масс в разных плоскостях . Требуется уравновесить деталь.
Для динамического уравновешивания такой детали должны выполняться два условия:
|
|
|
(3.32) |
Для выполнения этих двух условий к детали должны быть добавлены два уравновешивающих груза m,mII расположенных в плоскостях I и П. Плоскости, в которых располагаются уравновешивающие грузы, называются плоскостями уравновешивания. Они выбираются произвольно, но желательно их располагать ближе к опорам” При вращении детали возникают силы инерции и моменты инерции
|
|
|
|
|
от неуравновешенных масс m1 и m2 .
Перенесем
в плоскости уравновешивания эти силы,
добавив к ним еще и силы
![]() и
и
![]() ,
полученные при разложении моментов сил
инерции Mu1,
и Mu2
на пары сил в соответствии со следующими
выкладками
,
полученные при разложении моментов сил
инерции Mu1,
и Mu2
на пары сил в соответствии со следующими
выкладками
|
и |
|
откуда
|
и |
|
Тогда условие динамического равновесия будет выполнено, если будут равны нулю главные векторы сил, действующих в плоскостях уравновешивания.
Т.е.
![]()
если |
|
|
|
или
|
|
Где FyI , FyII - уравновешивающих масс в плоскостях I и П.
Графически
решая эти уравнения надо определить
величины
![]() и
и
![]() , а затем
найти уравновешивающие массы mI
и mII
или их радиусы-векторы
, а затем
найти уравновешивающие массы mI
и mII
или их радиусы-векторы
![]() и
и
![]() .
.
Направление радиусов-векторов и - также находится из векторного многоугольника.
Из
последних рассуждении можно заключить,
что при любом количестве неуравновешенных
масс динамическое уравновешивание
достигается двумя массами, установленными,
что и обеспечивает условия
![]() и
и
![]() .
.
3.7.4 Статическая и динамическая балансировка вращающихся масс.
Деталь, правильно спроектированная с точки зрения уравновешенности, может оказаться неуравновешенной вследствие неоднородности материала, неточности изготовления. Поэтому все быстровращающиеся детали подвергают опытному уравновешиванию на специальной машине. Такое опытное уравновешивание называется балансировкой. Она может быть статической и динамической.
Статическая балансировка выполняется на специальных призмах, расположенных параллельно, на которые помещается уравновешиваемая деталь или на пружинных весах (рис. 35).
В первом случае, когда центр масс смещен относительно оси, то деталь поворачивается пока центр масс не займет самое низкое положение. Добавлением масс предварительное крепление с помощью (пластилина) или удалением масс (высверливание) добиваются безразличного равновесия детали на призмах при любом ее повороте.
Во втором случае, балансируемую деталь помещают в опорах пружинного .рычага и поворачивают. По размаху рычага на шкале судят о величине и месте неуравновешенности.
При
тщательной балансировке можно добиться
смещения центра масс не менее
0,05 мм, Как
правило, статической балансировке
подвергаются детали плоские и вращающиеся
с малыми угловыми скоростями.
Рис 3.34. Балансировка на призмах Рис 3.35. Балансировка на пружинных весах
Динамическая неуравновешенность проявляется только при движении детали, поэтому динамическая балансировка выполняется только на движущейся детали.
Динамической балансировке подвергают детали большой длины и сложной формы, имеющие большую угловую скорость вращения.
Балансируют на специальных балансировочных станках и машинах различных конструкций.
При вращении деталь раскачивает основание, на котором закреплена, и по картине колебаний основания устанавливают величину неуравновешенности.
Станки и машины оснащены реагирующими приборами и электроникой, по которой устанавливают величину неуравновешенности.
В последнее время широкое распространение получили машины, имеющие возможность балансировать деталь при ее вращении путем напыления или испарения металла с помощью лазера.
Эти машины в сотни раз сокращают время и повышают точность балансировки, существенно повышают производительность труда и высвобождают людские резервы.
Лекция 14
План лекции.
3.7.5. Общие условия уравновешивания механизмов.
3.7.6. Уравновешивание шарнирного четырехзвенника.
3.8. Движение машины под действием заданных сил.
3.8.1. Режимы движения машины,
3.8.2. Характеристика внешних сил.
3.7.5. Общие условия уравновешивания механизмов.
Эту задачу рассмотрим на примере шарнирного четырехзвенного механизма.
При вращении ведущего звена общий центр масс механизма перемещается по замкнутому пути. Вследствие этого главный вектор и главный момент сил инерции периодически меняются по величине и направлению, возникающие при этом силы инерции передаются через стойку на фундамент, вызывая его быстрый износ, а в некоторых случаях могут привести к аварии.
Задача уравновешивания механизма сводится к уравновешиванию сил инерции его подвижных звеньев, т.е. к выполнению условий.
|
(3.33) |
В сложной машине, если эти условия выполняются для каждого из механизмов, то они выполняются и для машины в целом. Поэтому для уравновешивания машин достаточно обеспечить уравновешивание сил инерции каждого из её механизмов.
Для механизмов с нелинейной функцией положения (рычажных, кулачковых) тождественное выполнение условий (3.33) оказывается в большинстве случаев невозможным. При уравновешивании таких механизмов обычно ограничиваются выполнением только первого условия. Такое уравновешивание называется статическим. Естественно, что такое частичное выполнение условий уравновешивания далеко не всегда оказывается эффективным. Силы, действующие на стойку, приводятся в этом случае к главному моменту, который может вызывать интенсивные угловые колебания машины.
Рассмотрим, какими способами можно обеспечить обращение в нуль главного вектора сил инерции механизма. Как известно из кинетостатики
=
|
(3.34) |
Где ms - суммарная масса всех звеньев;
as - ускорение центра масс системы.
Для выполнения условия =0, необходимо, чтобы as=0, T.K. ms0.
Таким образом, при неизменном положении общего центра масс механизм будет статически уравновешен.