2 .5.4 Уравнения преобразования координат для конкретных кинематических пар,

Рассмотрим примеры. Пусть имеется кинематическая пара 5 клас­са .Требуется определить положение некоторой точки в системе S_i. Для данной кинематической пары:

С учетом этих уравнений

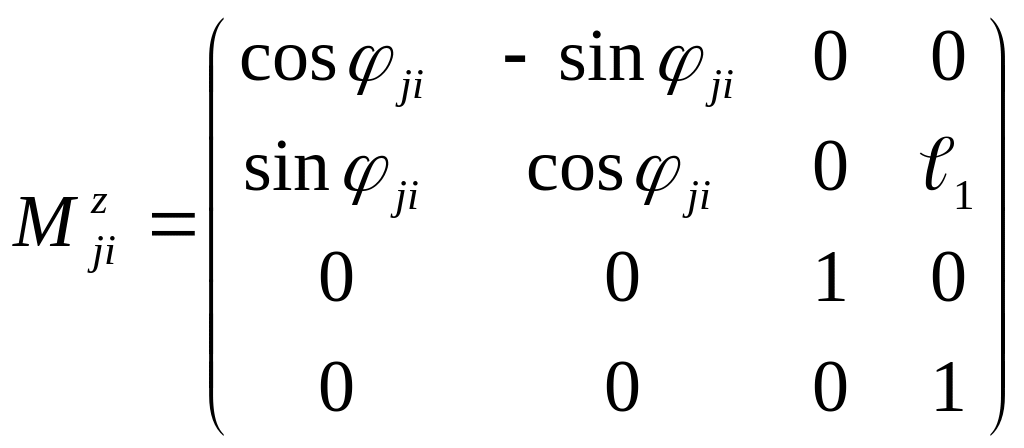
Положение точки Е в системе S_i

где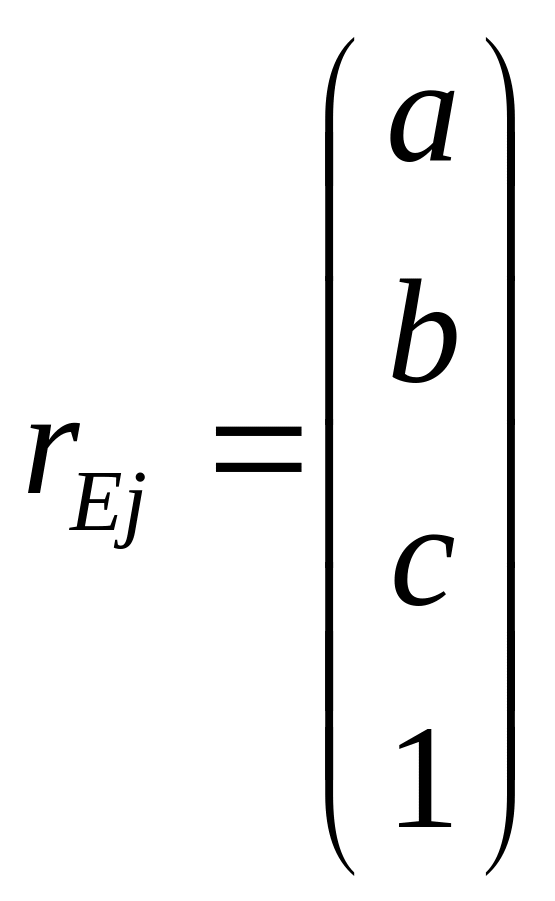

Для поступательной кинематической пары 5 класса / рис. 2. 15б/

С учетом этих уравнений любая матрица (2.17), (2.18), (2.19) дает одинаковое выражение вида: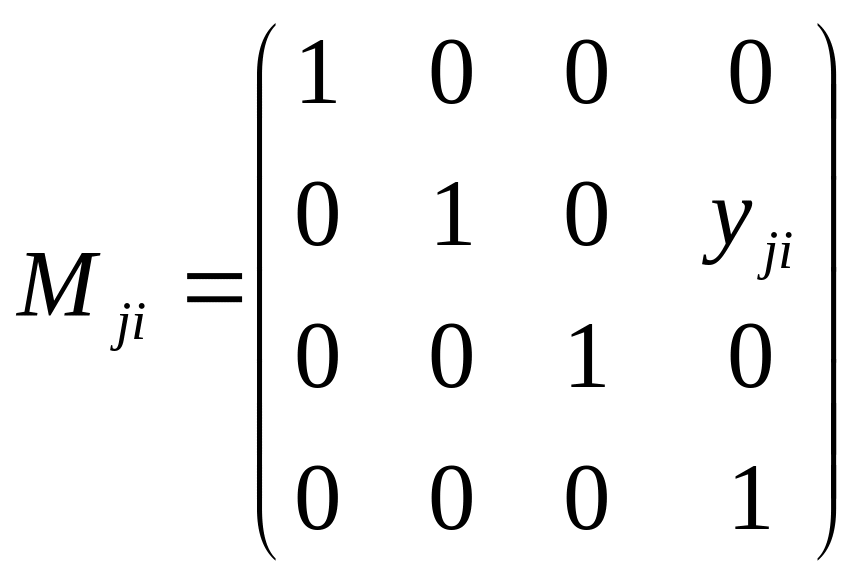

Т. е. для поступательной кинематической пары 5 класса ориентированной по любой из координатных осей первые три столбца матрицы одинаковы.

Положение точки в системе S_i:

где

2. 5. 5 Определение положения захвата пространственного манипулятора в неподвижной системе координат.

Полученные в предыдущем разделе выражения для матриц кине­матических пар позволяют определить положения точек звеньев любых пространственных кинематических цепей.

В качестве примера рассмотрим механизм манипулятора имеюще­го четыре степени свободы: возвратно-поступательное движение звена в вертикальном направлении по направляющим стойки. возвратно-вращательное движение звена 2 относительно звена I в горизонтальной плоскости и возвратно-поступательное и вращательное движение звена 3 с захватом относительно звена 2 в горизонтальном направлении.

С каждым звеном свяжем систему координат следующим образом:

по стойкой-системой так, чтобы ось Z₀ была направлена по оси поступательной пары А со звеном 1-систему так, чтобы ось Z₁ была направлена по оси вращательной пары со звеном 2 - систему так, чтобы ось -X₂ была направ­лена по оси поступательной пары С, а со звеном 3-систему оси которой параллельны осям системы S₂.

Запишем матричные преобразования координат точки E звена 3 от системы S₃ к системе S₀.

(2.20)

Рис. 2.14 Схема пространственного манипулятора имеющего четыре степени свободы

Для кинематической пары, состоящей из звеньев 2 и 3 уравнения

связи

Подставляя эти уравнения в выражение (2.18) ,а затем в (2.21) после преобразования получим

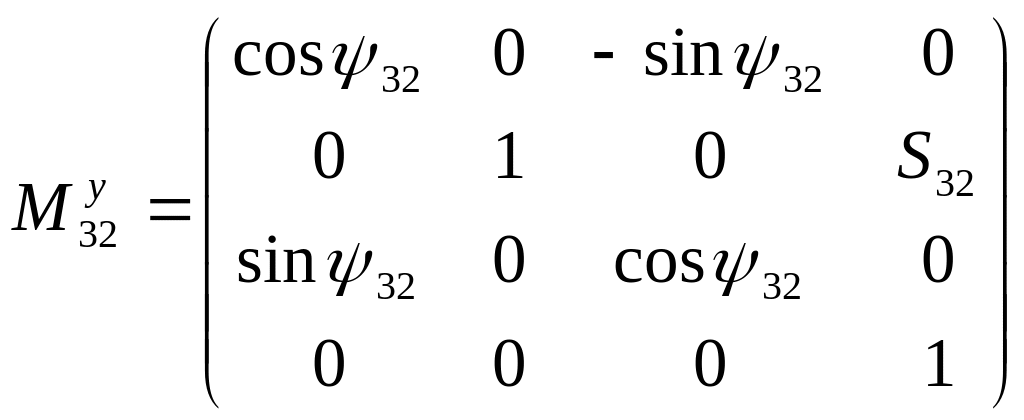(2.21)

Для кинематической пары из звеньев 2 и 1

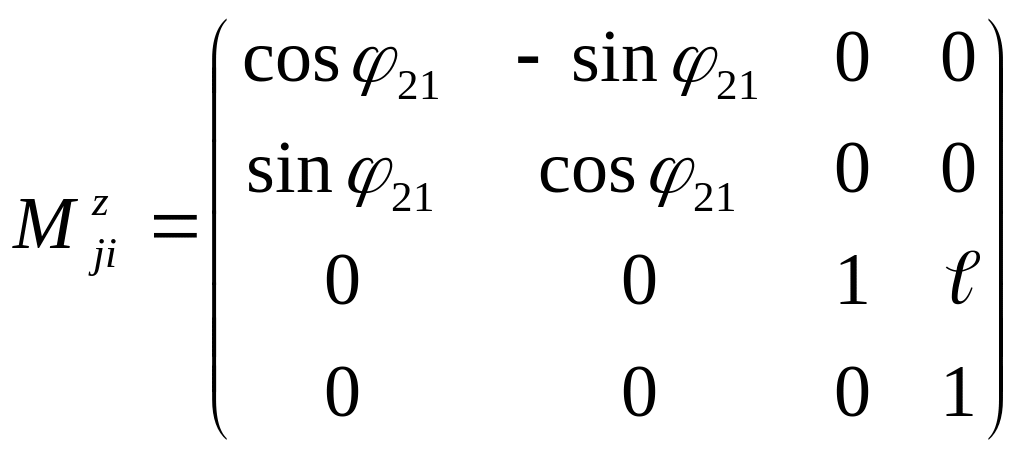(2.22)

Для кинематической пары из звеньев 1 и 0

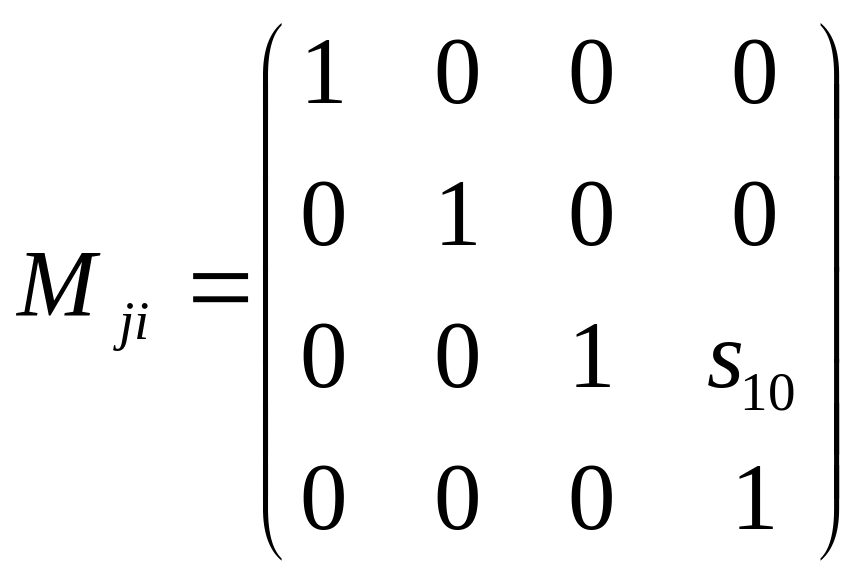(2.23)

После подстановки выражений (2.21), (2.22), (2.23) в ( .2.20 ) и применения матриц можно определить координаты точ­ки Е захвата в неподвижной системе S₀.

Параметры - переменные и задаются устройством управления манипулятора. Все другие параметры, в том числе и геометрические размера определяются конструкцией.

Лекция 8

План лекции

2.5.6 Определение положения точек в плоских механизмах

векторным методом.

2.5.7 Определение положений точек, скоростей и ускорений

точек и звеньев плоских механизмов. Аналоги скоростей.

2.5.6 Определение положений точек в плоских механизмах векторным методом.

П о этому методу каждое звено представляется вектором,т.е. кинематическая цепь заменяется векторным многоугольником.

Рис. 2.15 Векторный контур механизма.

Запишем условия замкнутости контура

После подстановки координат векторов получим

(2.24)

Из полученной системы уравнений можно найти и как

и , а затем

Для плоских механизмов векторный метод даёт достаточное число уравнений. Для пространственных - к ним нужно добавлять дополнительные уравнения, так как положение звена в пространстве определяется не одним вектором, а двумя. Поэтому векторный ме­тод эффективен только при исследовании плоских механизмов.

Наиболее универсальным является метод преобразования координат, позволяющий исследовать как плоские, так и пространственные механизмы с замкнутыми и разомкнутыми кинематическими цепями и автоматизировать процесс вычислений на компьютере, применяя стандартные программы преобразования координат звеньев, входящих в наиболее распространенные кинематические пары.