2.5 Метод преобразования координат.

Р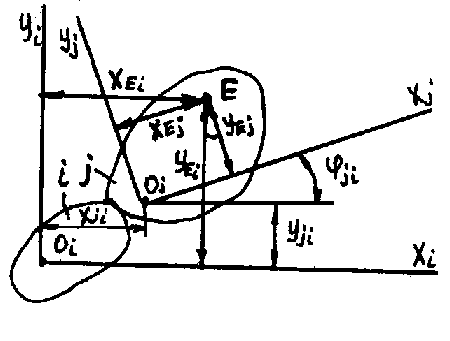 ассмотрим движение в плоскости. Пусть имеются два звена и , с каждым из которых свяжем свою систему координат и . Определим положение некоторой точки Е с известными координатами системы в координатной системе . Это положение описывается уравнениями преобразования координат следующего вида:

(2.1)

Систему уравнений (2.1) можно записать в матричной форме, доба­вив тождество 1=1. 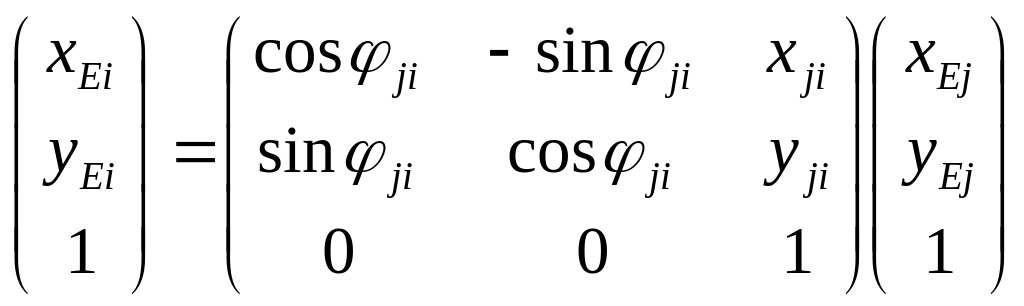(2.2)

или

Матрицы являются столбцами, характеризуют положение точки Е соответственно в системе и . Матрица характеризует движение звена j относительно i. При добавлении в эту матрицу уравнений связи кинематической пары, являющихся математическим выражением условий связи, можно получить матрицу конкретной кинематической пары.

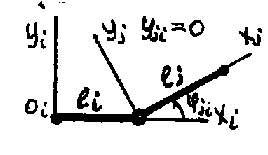
Для вращательной и поступательной кинематической пары 5 кл. матрицы 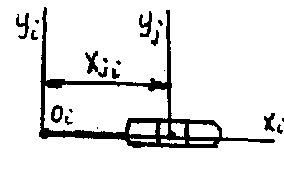имеют следующий вид:

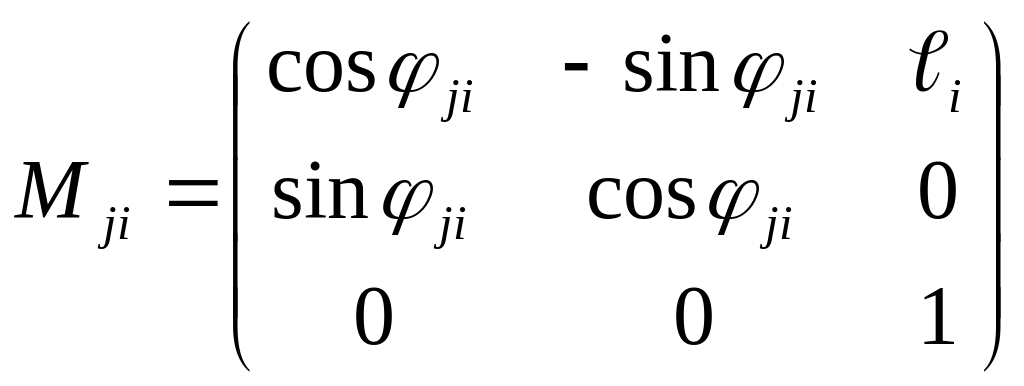
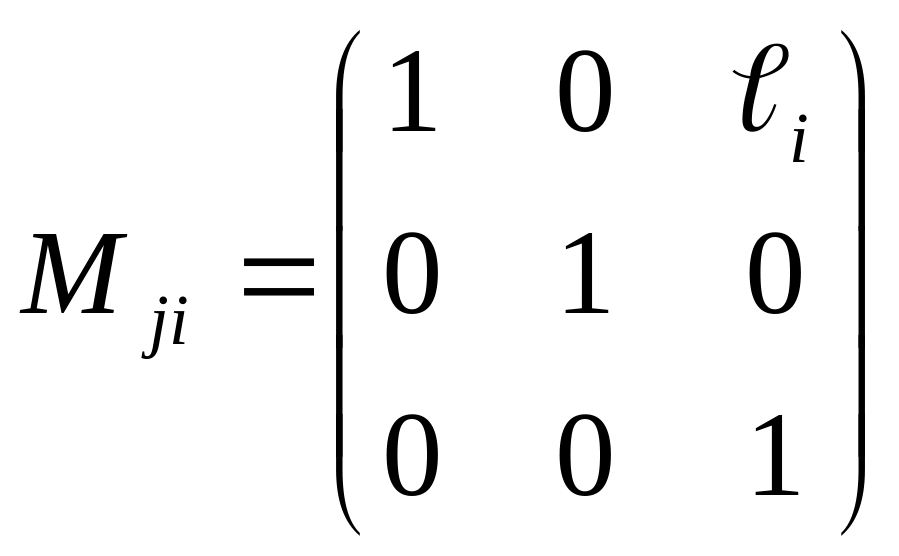
2.5.1. Определение положений точек в незамкнутых кинематических цепях.

Эта задача имеет самостоятельное значение для исследования механизмов манипуляторов и, кроме того. её решение может быть использовано для определения положений точек звеньев любых меха­низмов о замкнутыми кинематическими цепями.

Рассмотрим произвольную плоскую незамкнутую цепь, имеющую „n" подвижных звеньев (рис. 2.11) соединенных кинематическими парами пятого класса.

С неподвижным звеном и с каждым подвижным свяжем свою систе­му координат

Известны длины всех звеньев и координаты точки в системе , а также заданы обобщенные координаты

Т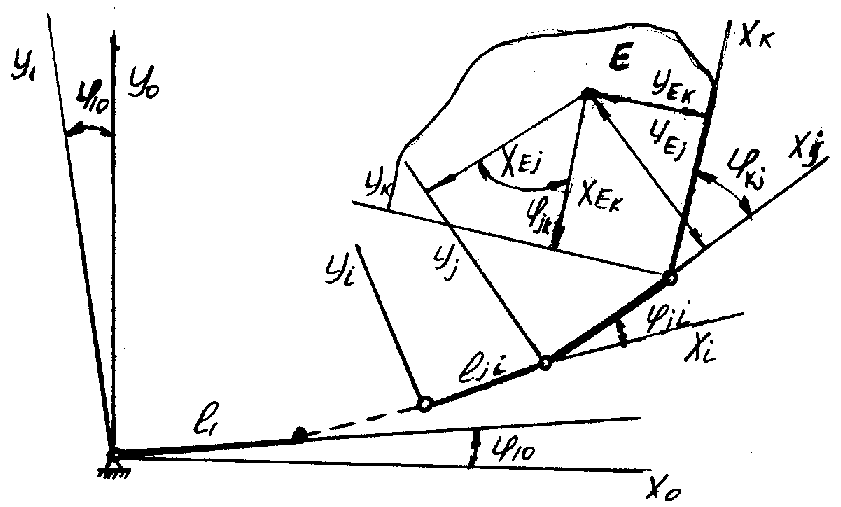 ребуется определить положение точки E в неподвижной системе координат , связанной со стойкой.

Рис. 2.11 Положение произвольной точки Е в незамкнутой кинематической цепи.

Для решения этой задачи произведем последовательный переход от координат точки Е в системе к её координатам в систе­ме .

На первом переходе определяем координаты точки Е в системе .

Уравнения преобразования координат при этом переходе в матричной форме

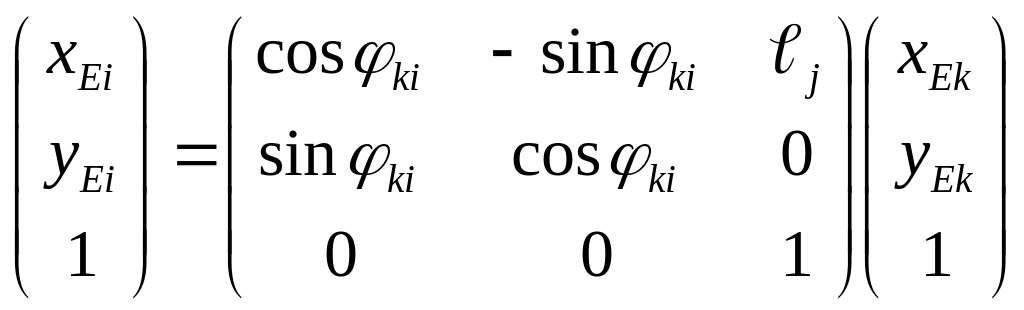
или (2.3)

При втором переходе к системе

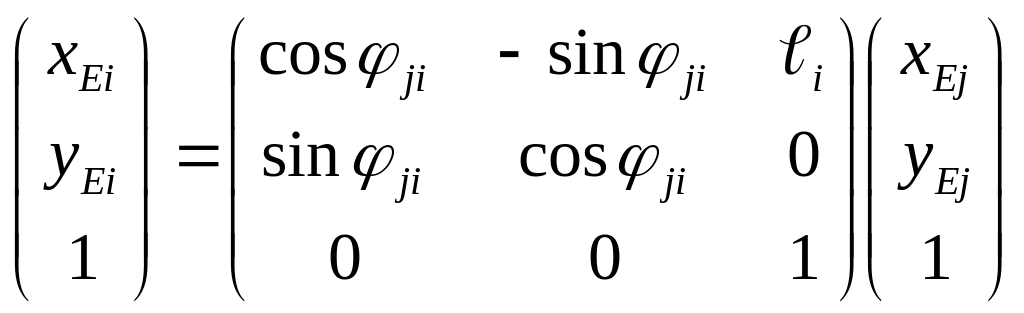
или (2.4)

Аналогично записываются уравнения преобразования

координат и на всех оставшихся переходах. Последний переход от системы S₁ к. S₀,

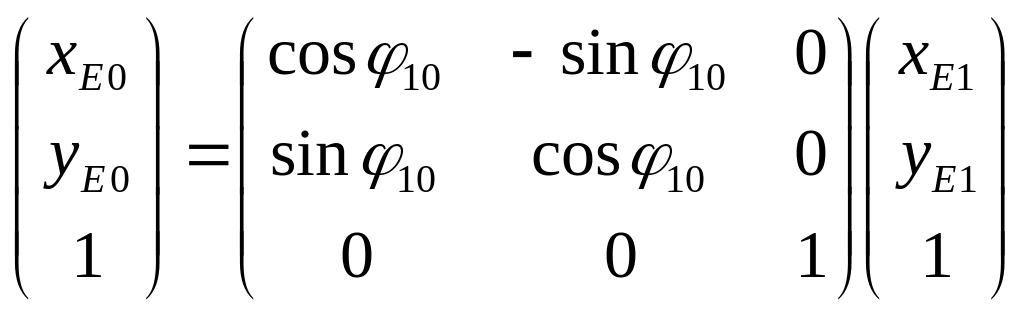
или (2.5)

Подставляя уравнение (2. 3 ) и ( 2.4) и далее в (2. 5) получим :

(2.6)

Рассмотрим схему меха­низма манипулятора» С каждым звеном свяжем свою систему координат. Известны геометрические размеры звеньев механиз­ма и определены: обобщен­ные координаты: и координаты некоторой точки Е в системе

Т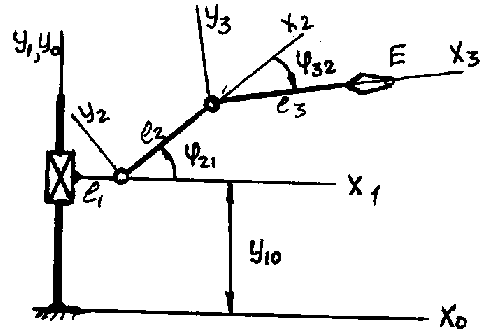 ребуется определить положение точки Е в неподвижной систе­ме координат S₀.

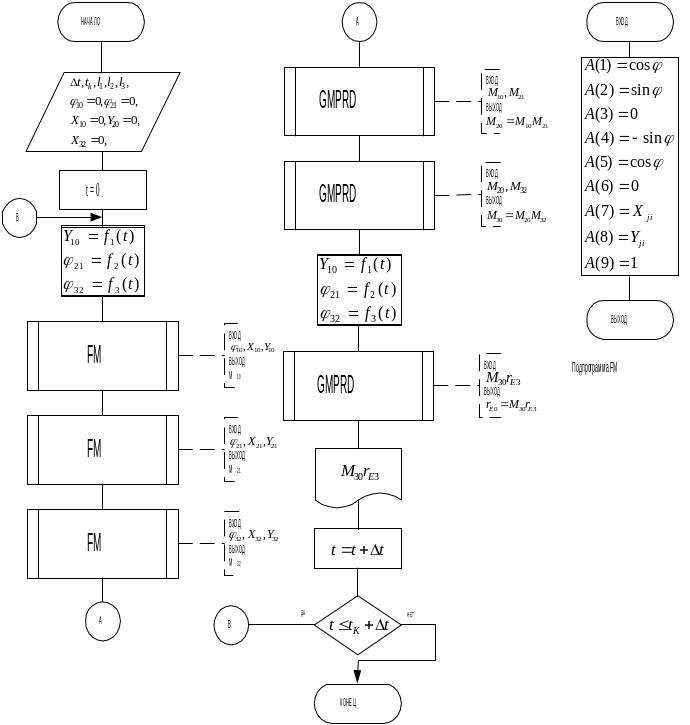
Для данной схемы в соответствии с формулой (2. 6)

Так как и

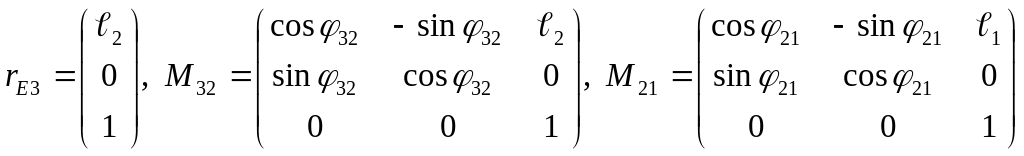
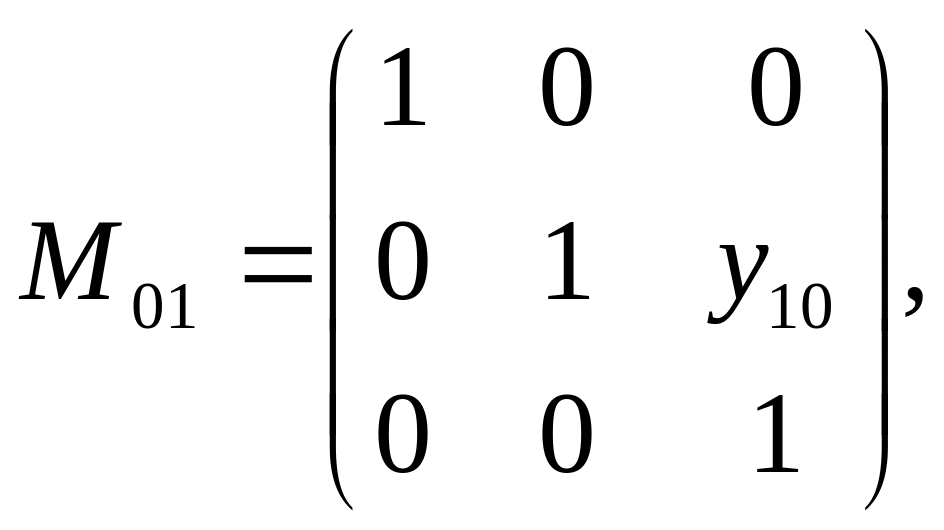представим

Полученные выражения могут быть использованы для состав­ления алгоритма, блок-схема которого может быть построена по следующей схеме