2.3.2 Построение планов ускорений.

Определяем ускорение точки А кривошипа по формуле

Здесь , - нормальное и тангенциальная составляющие. В нашем примере , поэтому

Нормальное ускорение определяется выражением

Этот вектор направлен параллельно ОА к центру вращения криво-

шипа (от точки А к точке 0 на звене).

Назначаем масштабный коэффициент плана ускорений и определяем длину вектора который будет представлять ускорение точки А

Из полюса плана ускорений P_a откладываем отрезок рис. 2.9. Здесь стрелка внизу показывает направление вектора от точки А к точке 0 на звене.

Для определения ускорения точки В опять разложим движение шатуна, как при построении плана скоростей. Тогда будем иметь

Величина	?			?
Направление

В этом уравнении и -нормальная и тангенциаль­ная составляющие относительного ускорения . Нормальная состав­ляющая вычисляется по формуле

Здесь - отрезок плана скоростей.

Начало и конец вектора на плане ускорений обозначим точками

а и n₂; n -говорит, что отложено нормальное ускорение, индекс 2 - что рассматривалось звено 2.

Полученное векторное уравнение может быть решено графически построением плана ускорений. Для этого из полюса проводим направление вектора абсолютного ускорения точки В параллельно направляющим ползуна В и далее строим векторную сумму по правой части уравнения. Пересечение известных по направлению векторов и ,и дает решение - точку плана ускорений.

Отрезок n₂b в принятом масштабе представляет вектор , величина которого равна

Зная величину и направление тангенциальной составляющей отно­сительного ускорения точек В и А, можно определить величину и направление углового ускорения шатуна . Его величина определяется выражением

Для определения направления - вектор показываем выходящим из точки В на звене.

Свойства планов ускорений.

Эти свойства аналогичны свойствам планов скоростей и доказы­ваются аналогично.

1. Векторы абсолютных ускорений всех точек берут начало в одной точке - полюсе . Вытекает из определения.

2. Отрезки, соединяющие концы векторов абсолютных ускорений при принятом масштабном коэффициенте , представляют относительные ускорения точек. Например,

3. Одноименные фигуры на звене и плане ускорений подобны, а одноименные отрезки пропорциональны и повернуты в сторону углового ускорения звена на одинаковый угол (180°- ).

Для доказательства определим угол между векторами (отрезок ) и . Первый из них параллелен отрезку АВ на звене, второй представлен отрезком ав на плане ускорений.

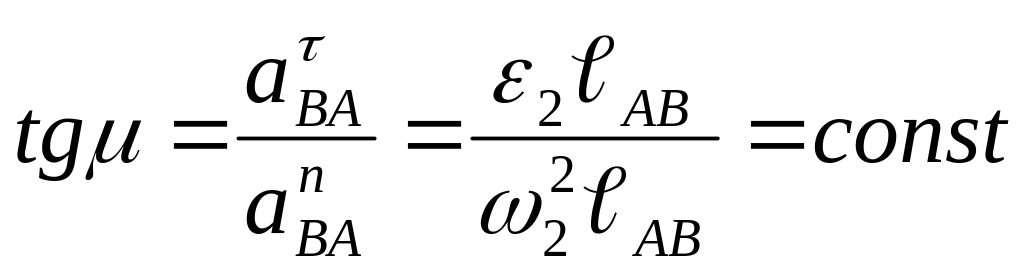
Сюда не входят координаты точек, поэтому для всех одноименных отрезков данного звена этот угол одинаковый. В таком случае одноименные фигуры подобны и составлены из пропорциональных отрезков.

Последнее позволяет при известных ускорениях двух точек звена найти ускорение любой другой точки этого звена. Например, для определения ускорения точки С на стороне плана ускорений строится подобный АВС на звене. При этом следует помнить, что обвод контуров одноименных фигур должен производиться в одинаковом направлении.

Для определения ускорения точки S₂ составляется пропорция

Абсолютные ускорения точек А, В, С, в м/с определяются выражениями

В нашем примере у шатуна АВ известны величины и направление скорости и ускорения точки А и направление (траектория) скорости точки В. Такие исходные данные необходимы и достаточны для опре­деления ускорения любой другой точки.

4. Всем т очкам, ускорение которых равно нулю, на плане ускоре­ний соответствует одна точка - полюс .

Лекция 6

План лекции

2. 4 Аналитические методы кинематического анализа.

2. 5 Метод преобразования координат.

2.5.1 Определение положений точек в незамкнутых кинематических цепях.

2.5.2 Определение положений точек в замкнутых кинематических цепях.

2. 4. Аналитические методы кинематического анализа.

Рассмотренные ранее графические методы кинематического анализа применяются в основном при исследовании плоских меха­низмов, т. к. для пространственных механизмов они, базируясь на методах начертательной геометрии, теряют главное своё преимущество- простоту и наглядность.

Аналитические методы сложнее графических, но более точны и оправданы при использовании вычислительной техники.

При работе с графическими методами исследователь вручную проводит все вычисления и построения, начиная с постановки зада­чи и кончая получением конечного результата. При использовании аналитических методов исследователь составляет алгоритм и програм­мирует, а все необходимые расчеты производятся на компьютере. Экономия времени при использовании аналитических методов значительная. Правильно составленные алгоритм и программа позво­ляют, варьируя геометрическими размерами и другими параметрами, просчитывать множество вариантов механизмов.

Кинематический анализ характеристик множества вариантов ме­ханизма необходим для решения задач синтеза. т. е. выбора оптимального варианта механизма. В данном случае количественные изменения (т. е. свойства множества вариантов механизмов) переходят в новое качес­тво (т. е. создание оптимального варианта механизма), в чем и отра­жается действие объективного закона диалектики-перехода количества в качество.

Противоположные понятия, как анализ и синтез оказываются во взаимосвязи и взаимообусловленности, как и все другие категории диалектики.

Аналитические методы кинематического анализа делят на две группы:

1 Метод замкнутых векторных контуров проф. Зиновьева, который применяется в основном для исследования плоских механизмов с замкнутыми кинематическими цепями.

2. Метод преобразования координат проф. Морошкина наиболее универсален, одинаково просто используется при исследовании как плоских, так и пространственных механизмов с замкнутыми и незамкнутыми кинематическими цепями.

Оба метода несложно реализуются на компьютере.