9.2. Физический смысл изохорно-изотермического и изобарно-изотермического потенциалов

К аждая характеристическая функция имеет свою область применения.

Рассмотрим физический смысл изохорно-изотермического потенциала в уравнениях и . Представим себе, что рассматриваемая адиабатная система А является частью другой адиабатной системы В (среды) (рис. 26). Температура обеих систем Т. Внутри этих систем протекают различные процессы при постоянной температуре. Обозначим изменение внутренней энергии и энтропии системы А через dU и dS, а изменение внутренней энергии и энтропии среды В – через dU' и dS'. По закону сохранения энергии, внутренняя энергия всей сложной замкнутой системы неизменна: . На основании второго закона термодинамики энтропия сложной системы или должна оставаться постоянной, или в случае необратимых процессов должна увеличиваться: . Предположим, что система А совершает работу δL над телами среды В и при этом передает среде В некоторое количество теплоты, вследствие чего энтропия среды повысится на dS'. Тогда на основании термодинамического тождества изменение внутренней энергии среды В составит .

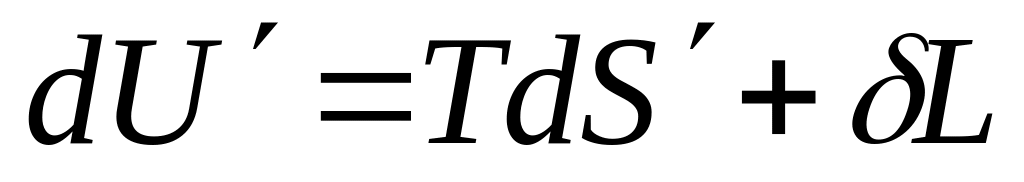Работа имеет положительный знак, если она совершается над телами среды и увеличивает энергию ее тел. Из трех приведенных уравнений находим

.

Все величины в этом уравнении относятся к системе, а не к среде.

Так как температура сложной системы постоянна, то уравнение можно представить так:

.

Выражение в скобках есть не что иное, как изохорно-изотермический потенциал системы F, поэтому для всяких изотермических процессов

.

Для обратимых изотермических процессов

или .

При изотермических обратимых процессах работа, совершаемая системой, равна уменьшению изохорно-изотермического потенциала.

Из уравнений и следует, что .

Или при постоянной температуре .

Величина есть полученная системой теплота, поэтому данное уравнение указывает, что работа в изохорно-изотермическом процессе совершается не только за счет внутренней энергии, но и за счет теплоты среды. Работы равна разности или . Работа равна уменьшению изохорно-изотермического потенциала F. Изохорно-изотермический потенциал системы есть часть ее энергии, которая в изотермическом процессе превращается во внешнюю работу.

Таким образом, общую энергию системы U можно представить в виде суммы двух частей уравнения:

.

На внешнюю изотермическую работу расходуется только изохорно-изотермический потенциал. Часть TS выделяется в виде теплоты и в работе не участвует. Эту часть Гельмгольц назвал связанной энергией.

При обратимом процессе работа, производимая телом при переходе из одного состояния в другое, является максимальной. Поэтому если уравнение проинтегрировать между начальным и конечным состоянием системы, то . Максимальная работа, производимая системой в изотермическом процессе, равна разности изохорно-изотермических потенциалов в этих двух состояниях.

При необратимом изотермическом процессе работа L, совершаемая системой, меньше L_МАКС. Из уравнения следует, что . Или после интегрирования получаем . Из этого неравенства видно, что изохорно-изотермический потенциал системы при необратимом изотермическом процессе возрастает на меньшую величину по сравнению с внешней работой. Уравнения и можно объединить в одно:

.

Знак равенства относится к обратимым процессам, знак «меньше» – к необратимым.

Таким образом, изохорно-изотермический потенциал F является мерой работоспособности системы при T = const.

Если необратимый процесс протекает при постоянных объеме и температуре без совершения внешней работы, то общая работа системы L равна нулю, и уравнение примет вид

.

Изохорно-изотермический потенциал системы при постоянных объеме и температуре в необратимом процессе всегда убывает, а в обратимом остается величиной постоянной.

Применяя уравнение , можно получить другое уравнение максимальной работы:

.

Пусть система переходит из первого во второе состояние, тогда

и .

Разность изохорно-изотермических потенциалов

;

.

В изохорном процессе , поэтому – уравнение максимальной работы Гиббса – Гельмгольца при постоянных Т и V.

Работа расширения системы, преодолевающая внешнее давление р, равна . Подставляя в уравнение это выражение, получим

.

Или, применяя уравнение или F = U – TS, находим

.

В рассматриваемой системе давление постоянно, поэтому последнее уравнение можно представит в виде . Выражение в скобках есть изобарно-изотермический потенциал, поэтому

или .

Отсюда следует, что в системах, находящихся при постоянной температуре и постоянном давлении, обратимые процессы протекают при постоянной величине изобарного потенциала. При протекании в системе необратимых процессов изобарно-изотермический потенциал всегда уменьшается. Необходимо отметить, что протекание процесса при постоянных температуре и давлении однородной системы, находящейся в среде постоянного давления и температуры, возможно лишь при неравенстве параметров системы с давлением и температурой среды. В неоднородной системе, состоящей из двух фаз вещества, для которой давление и температура не являются независимыми параметрами, могут протекать обратимые процессы при равенстве температуры и давления системы и окружающей среды.

Уравнение работы при изобарно-изотермическом процессе можно представить в развернутом виде

или .

Из уравнения следует и .

Подставляя значения энтропии в уравнение максимальной работы, получим

или .

Но в изобарном процессе , а . Поэтому

–

уравнение максимальной работы Гиббса – Гельмгольца при постоянных Т и р.

В системе при необратимом процесс, протекающем при постоянных давлении и температуре, полезная работа равна . Т. е. она меньше максимальной работы на величину произведения абсолютной температуры среды на приращение энтропии системы. Величину называют потерей полезной работы из-за необратимости процесса.

Характеристические функции U (V, S), I (p, S), F (T, V), Z (p, T), полностью определяющие все термодинамические свойства системы, называются также термодинамическими потенциалами. Термодинамическим потенциалом называется такая характеристическая функция, убыль которой в равновесном процессе, протекающем при постоянстве определенной термодинамической пары термодинамических параметров (Т и V, T и p, S и U), равна полной работе, произведенной системой, за вычетом работы против внешнего давления. Каждый из термодинамических потенциалов является функцией состояния системы.

Известно, что при обратимом процессе для перевода тела из одного состояния в другое необходимо затратить минимальную работу, при этом само тело при переходе совершает максимальную работу. Поэтому с помощью термодинамических потенциалов можно определить максимальную работу при различных независимых переменных.

Действительно, при постоянных независимых переменных S и V характеристической функцией и термодинамическим потенциалом является внутренняя энергия U (изохорно-изоэнтропический потенциал), а или . При изохорно-изоэнтропическом процессе максимальная работа изменения объема равна убыли внутренней энергии тела.

При постоянных независимых переменных S и p характеристической функцией и термодинамическим потенциалом является энтальпия I (изобарно-изоэнтропический потенциал), а или .

При изобарно-изоэнтропическом процессе максимальная полезная внешняя работа равна убыли энтальпии тела.

При постоянных независимых переменных Т и V характеристической функцией и термодинамическим потенциалом является изохорно-изотермический потенциал , или .

При изохорно-изотермическом процессе максимальная работа изменения объема равна убыли изохорно-изотермического потенциала.

При постоянных независимых переменных Т и p характеристической функцией и термодинамическим потенциалом является изобарно-изотермический потенциал, а или .

При изобарно-изотермическом процессе максимальная полезная внешняя работа равна убыли изобарно-изотермического потенциала.

Таким образом, знание хотя бы одного термодинамического потенциала позволяет определить термические и калорические свойства термодинамической системы. При практических исследованиях чаще всего применяют два потенциала: изохорно-изотермический и изобарный, поскольку независимые переменные Т, V и Т, р, при которых они являются потенциалами, легко могут быть получены из эксперимента. Все термодинамические потенциалы являются аддитивными и однозначными функциями состояния, а их убыль при соответствующих условиях определяет работу действующих на систему сил.