Контрольные вопросы

1. Можно ли в круговом процессе превратить всю подведенную теплоту в работу?

2. Основные формулировки второго закона термодинамики.

3. Какие требуются условия для создания непрерывного процесса превращения теплоты в работу?

4. Какие бывают циклы?

5. Что называется термическим КПД?

6. Вывод выражения для термического КПД обратимого цикла Карно.

7. В каких случаях термический КПД цикла Карно может быть равен единице?

8. Можно ли получить термический КПД цикла теплового двигателя, больший термического КПД цикла Карно?

9. Обратимый цикл Карно.

10. Что такое холодильный коэффициент и как он определяется?

11. Свойство обратимых циклов Карно и первый интеграл Клаузиуса.

12. Свойства необратимых циклов Карно и второй интеграл Клаузиуса.

13. Каково изменение энтропии в замкнутой адиабатной системе, если в ней протекают обратимые и необратимые процессы?

Задача

1 кг воздуха совершает прямой обратимый цикл Карно в пределах температур t₁ = 627 С и t₂ = 27 С, при этом наивысшее давление составляет 6 МПа, наинизшее – 0,1 МПа. Определить параметры состояния воздуха в характерных точках цикла, работу, термический КПД цикла и количество подведенной и отведенной теплоты.

Решение

Согласно рис. 20, определим параметры воздуха в характерных точках цикла.

Точка 1. р₁ = 6 МПа; Т₁ = 273 + 627 С = 900 К. Удельный объем газа находим из характеристического уравнения: .

Точка 2 (участок 1–2 – изотермическое расширение). Т₂ = Т₁ = 900 К.

Из уравнения адиабаты (линия 2–3) ,

откуда МПа.

Из уравнения изотермы (линия 1–2) получаем

.

Точка 3. р₃ = 0,1 МПа; Т₃ = 300 К; .

Точка 4. Т₄ = 300 К; из уравнения адиабаты (линия 4–1) имеем:

Тогда МПа.

Из уравнения изотермы (линия 3–4) получаем .

.

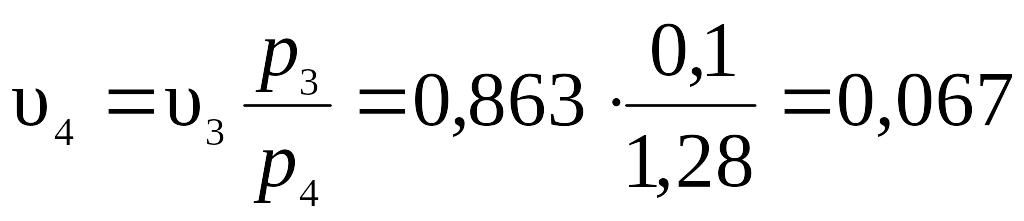
Термический КПД цикла, согласно формуле

Подведенное количество теплоты:

.

Отведенное количество теплоты:

.

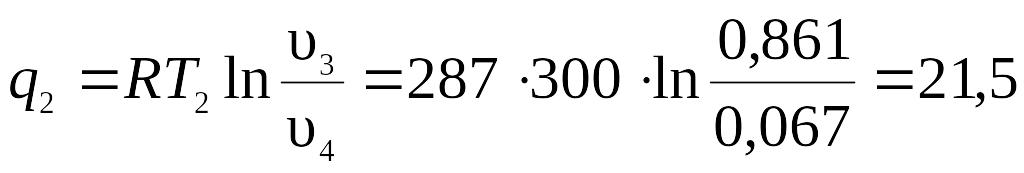Работа цикла:

.

Для проверки можно воспользоваться формулой

9. Характеристические функции и термодинамические потенциалы. Равновесие систем

9.1. Характеристические функции состояния

Характеристические функции состояния – функции, с помощью которых и посредством их производных разных порядков могут быть явно выражены все термодинамические свойства системы, в том числе уравнения состояния, уравнения для определения теплоемкостей и термодинамические потенциалы.

К характеристическим функциям относятся:

1. внутренняя энергия U (V, S);

2. энтальпия I (p, S);

3. изохорно-изотермический потенциал F (T, V);

4. изобарный потенциал Z (p, T);

5. энтропия S (V, U);

6. объем V (S, U).

Если эти функции выражены в аналитической форме через независимые параметры системы, то можно в явной форме получить все основные термодинамические величины, характеризующие данную систему.

Характеристические функции аддитивны. Значение их для сложной системы равно сумме значений функций для отдельных частей. Дифференциалы характеристических функций являются полными дифференциалами. Исходя из выражений первого и второго начал термодинамики, получим

–

это выражение называется термодинамическим тождеством. Оно содержит только параметры функций состояния системы, их дифференциалы и относится к обратимым процессам. В переменных р и Т термодинамическое тождество примет вид:

.

Это два самых общих уравнения термодинамики. Они связывают между собой пять переменных величин: T, S, U, p, V, определяющих состояние системы. Эти пять параметров образуют между собой 10 различных сочетаний, из которых имеют значение только четыре:

– внутренняя энергия;

– энтальпия;

– изохорно-изотермический потенциал;

– изобарно-изотермический потенциал (изобарный).

Внутренняя энергия U является характеристической функцией при независимых переменных S и V. Если система совершает работу, то уравнение изменения внутренней энергии примет вид:

.

Энтальпия I является характеристической функцией при независимых переменных S и p. Получаем:

.

Изохорно-изотермический потенциал Z является характеристической функцией T и V. Вычитая из правой и левой частей в уравнении по d(TS), получаем:

;

и . Откуда или .

Величина TS является функцией состояния и называется связанной энергией.

Изобарный потенциал Z является характеристической функцией Т и р. Прибавив к левой и правой частям уравнения по d(pV), получим

;

;

или .