23°. Векторное произведение векторов. Свойства векторного произведения векторов.

Опр.Векторным произведение, вектора и наз. вектор * ([ , ]) для которого: 1) длина | * |=| || |sin ϕ , ϕ <( , ); 2) * L , * L ; 3) , , * – правая тройка векторов. Правило правой руки.

Если векторы и коллинеарны или один из них равен ,то * = ;

Сво-ва:

1) Длина векторного произведению равна S параллелограмма построенного на векторах и отложенных от одной точки: | * |= S парал.;

2) * = - * ;

3) (λ )* = λ ( * );

*(λ )= λ ( * );

4) *( ) = ( * )+ ;

*( ) = ( )+ ;

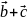24. Выражение векторного произведения векторов, заданных прямоугольными координатами.

Пусть (О, , , );

( a1, a2, a3); = а1 +а2 +а3 ; (b1, b2, b3), = b1 +b2 +b3 ;

* =(а1 +а2 +а3 )*(b1 +b2 +b3 )= (a2b3-a3b2) -(a1b3-a3b1) +(a1b2-a2b1) ; * =

* =

* =

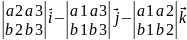
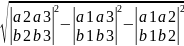
25°. Смешанное произведение векторов. Теорема о вычислении объема параллелепипеда, построенного на трех векторах.

Опр. Смешанным произвед. векторов , и наз. число равное скалярному произведению векторного произведению =( * ) .

Теорема: Пусть , , – некомпланарные векторы. V – параллелепипеда, построенного на векторах , и , отложенных от одной точки, равен смешанному произвед. этих векторов, взятых со знаком «+», если , , – правая тройка, «-» если , , – левая тройка.

V =Sосн.h; Sосн=| || |sin ϕ=| * |;

h=|AH|= cos(HAA1)=<( , * );

V=| * || |cos( , )= | * | = .

Следствие: векторы компланарны, тогда и только тогда, когда их смешанное равно нулю.

26. Выражение смешанного произведения векторов, заданных прямоугольными координатами.

Пусть (О, , , );

(a1, a2, a3); (b1, b2, b3); (c1, c2, c3);

=( * ) =c1 -c2 +c2

=

Св-ва:

=- = =-

27°. Уравнение прямой на плоскости, проходящей через данную точку в данном направлении (каноническое уравнение прямой).

Рассмотрим некоторую прямую на плоскости. Введём аффинную СК (О, , ), М0-некоторая точка ϵ прямой ∆ и вектор параллельный этой прямой ≠0.

Опр: ненулевая параллельная прямая назыв направляющим вектором.

Некоторая точка и ненулевой вектор определяют прямую М0(х₀,у₀), ( , )

Пусть точка М- произвольная точка прямой М(х, у), то М ϵ ∆ ⟺ ǁ , (х-х₀, у-у₀), ( , ) ǁ из этого (х-х₀)÷а₁=(у-у₀)÷а₂ – каноническое ур-ние прямой.

28. Общее уравнение прямой на плоскости.Параметрическое уравнение прямой на плоскости.

Общее ур-ниепрямой:

Опр: линейным ур-нием первой степени от двух переменных назыв. ур-ниеАх+Ву+С=0, где А²+В²≠0.

Теорема: всякое линейное ур-ние первой степениАх+Ву+С=0 определяет ур-ние прямой в некоторой аффинной СК, и наоборот всякую прямую в некоторой аффинной СК можно задать ур-ниемАх+Ву+С=0.

Док-во:⟹ Пусть Ах+Ву+С=0, А≠0, В≠0, х=(-Ву-С)÷А. х÷(-В)=(у+С÷В)÷А- каноническое ур-ние некоторой прямой. М₀(0;-С÷В), (-В;А). А≠0, В=0: 0*у+Ах+С=0, х=-С÷А, . ⟸Пусть ∆-некоторая прямая, ǁ∆. (О, , )-аффинная СК, тогда (х-х₀)÷а₁=(у-у₀)÷а₂ –каноническое ур-ние прямой, а₂х-а₁у+а₁у₀-а₂х₀=0, тоАх+Ву+С=0, ≠ , а₁²+а₂²≠0⟹А²+В²≠0. Ах+Ву+С=0- общее ур-ние прямой, (-В, А)- направляющий вектор. Пусть Ах+Ву+С=0 ур-ние прямой в прямоугольной СК. (-В, А), (А, В), * =А*(-В)+В*А=0⟹ ⏊ .

29°. Уравнение прямой на плоскости, проходящей через две точки. Уравнение прямой на плоскости в отрезках.

ǁ∆, -направляющий, М1(х₁,у₁), (х₂-х₁, у₂-у₁), (х-х₁)÷(х₂-х₁)=(у-у₁)÷(у₂-у₁)- ур-ние прямой проходящей через две точки. (х-а)÷(0-а)= (у-0)÷(b-0), bx-ab=-ay, bx+ay=ab, 0 не принадлежит ∆, (х÷а)+(у÷b)=1- ур-ние в отрезках.

30°. Уравнение прямой на плоскости с угловым коэффициентом.

Рассмотрим ∆, М₀ϵ∆, ǁ∆, М₀(х₀,у₀), ( , ), а1≠0. Будем рассматривать прямые не параллельные оси ординат Оу.

Опр: Пусть ( , )ǁ∆, а1≠0, к=а₂÷а₁-угловой коэффициент прямой. Рассмотрим (х-х₀)÷а₁=(у-у₀)÷а₂, у=(а₂÷а₁)*х+у₀-(а₂÷а₁)*х₀, тогда у=кх+b-ур-ние прямой с угловым коэффициентом. Рассмотрим в прямоугольной СК к=а₂÷а₁=tgα.

31. Частные случаи расположения прямой на плоскости относительно системы координат.

Пусть(О, , , ), Ах+Ву+С=0- некоторая прямая, (-В, А)-направ вект: 1.А=0 ⟹, (-В, 0) ⟹Ву+С=0 ⟹у=-С÷В прямая параллельная оси Ох; 2.В=0 ⟹ , (0, А) ⟹Ах+С=0⟹х=-С÷А прямая параллельная оси Оу; 3.С=0 ⟹, (-В, А)⟹Ах+Ву=0 проходит черех начало координат; 4.А=0,С=0 ⟹Ву=0 или у=0: ур-ние оси Ох; 5.В=0, С=0 ⟹ Ах=0 или х=0: ур-ние оси Оу.

32. Взаимное расположение двух прямых на плоскости.

Пусть (О, , ), ∆₁:А₁х+В₁у+С₁=0, ∆₂:А₂х+В₂у+С₂=0.

1)∆₁ǁ∆₂;

2) ∆₁=∆₂;

3)∆₁∩∆₂=0(пересекаются).

Теорема:

Пусть ∆₁:А₁х+В₁у+С₁=0, ∆₂:А₂х+В₂у+С₂=0:

1. ∆₁∩∆₂⟺А₁÷А₂≠В₁÷В₂;

2.∆₁ǁ∆₂⟺ А₁÷А₂=В₁÷В₂≠С₁÷С₂;

3. ∆₁=∆₂⟺ А₁÷А₂=В₁÷В₂=С₁÷С₂.

33°. Расстояние от точки до прямой на плоскости.

Пусть (О, , )- прямоугольная СК, Р(х₀, у₀), ∆:Ах+Ву+С=0, М(х,у)-произвольная точка прямой, (А, В)-нормальный вектор, (х-х₀, у-у₀), = *cos∠NPM= *cos∠NPM= = = = 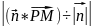÷ = ÷ ÷ =(Ax₀+By₀+C)÷ , p(P,∆)= C)÷( )

34°. Угол между прямыми на плоскости.

Пусть (О, , ), ∆₁:А₁х+В₁у+С₁=0, ∆₂:А₂х+В₂у+С₂=0, (A₁, B₁), (A₂, B₂). Угол между ∆₁ и ∆₂ либо равен углу между и , либо 𝜑=180⁰-∠( , ). cos𝜑=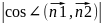 = = (A₁*A₂+B₁*B₂)÷( * ), cos𝜑=

35°. Уравнение плоскости, проходящей через данную точку параллельно двум векторам.

Пусть плоскость π-некоторая плоскость, М₀ϵπ, ǁπ, ǁπ, не параллелен . Введём СК (О, , , ), М₀(х₀,у₀,z₀), М(х, у,z)-произвольная точка ϵ π, (х-х₀, у-у₀, z-z₀), , , -компланарные. =0 – ур-ние плоскости, проход через точку ǁ двум векторам.

36.Общее ур-ние плоскости. Параметрическоеур-ние плоскости.Пусть π- некоторая плоскость, М₀ϵπ, не параллельно , ǁπ , ǁπ. Введём СК (О, , , ), М₀(х₀,у₀,z₀), М(х,у,z)-произвольная точка ϵ π, (х-х₀, у-у₀, z-z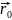₀), = , (х₀,у₀,z₀), 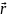= , (x,y,z), = + ; α,β-числа, =α* +β* , r=r₀+ α* +β* – параметрическое ур-ние в векторной форме. Не сложно заметить, что получится следующее: – параметрическое ур-ние в координатной форме.

Опр: Ур-ние видаАх+Ву+Сz+D=0, где A,B,C,D- действительные числа А²+В²+С²≠0, назыв линейным ур-нием первой степени от трёх переменных.

Теорема: всякая линейное ур-ние первой степениАх+Ву+Сz+D=0 является ур-нием некоторой плоскости в аффинной СК и наоборот. Док-во:⟹Ах+Ву+Сz+D=0- ур-ние, (х₀,у₀,z₀)-некоторое решение, Ах₀+Ву₀+Сz₀+D=0-верное равенство. Легко заметить: А*(х-х₀)+В*(у-у₀)+С*(z-z₀)=0, A≠0, A²*(х-х₀)+A*В*(у-у₀)+A*С*(z-z₀)=0,

Легко заметит: =0 –ур-ние плоскости проходящей через М(х₀,у₀,z₀) и двумя векторами (-В,А,0), (-С,0,А). ⟸π-плоскость (О, , , ), =0,

(а₂b₃-b₂a₃)(x-x₀)+(b₁a₃-a₁b₃)(y-y₀)+(a₁b₂-b₁a₂)(z-z₀)=0, A(x-x₀)+B(y-y₀)+C(z-z₀)=0, D=-Ax₀-By₀-Cz₀, Ax+By+Cz+D=0.