
- •1°. Понятие матрицы. Элементарные преобразования матрицы.
- •2. Ступенчатая матрица. Теорема о приведении матрицы к ступенчатой матрице.
- •3°. Системы линейных уравнений (слу). Решение слу. Эквивалентные слу. Однородные слу.
- •4. Метод Гаусса решения систем линейных уравнений.
- •5°. Определители второго и третьего порядков.
- •7. Миноры и их алгебраические дополнения. Теорема Лапласа.
- •8°. Обратная матрица.
- •9. Правило Крамера решения систем линейных уравнений.
- •10°. Направленный отрезок. Эквивалентные направленные отрезки. Понятие вектора. Угол между векторами. Коллинеарные и компланарные векторы.
- •11°. Операции над векторами. Свойства операции над векторами.
- •12. Понятие линейной зависимости векторов. Линейно независимые векторы. Необходимое и достаточное условие коллинеарности двух векторов. Необходимое и достаточное условие компланарности трех векторов.
- •13°. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам.
- •13. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам.
- •14. Теорема о разложении вектора в пространстве по трем некомпланарным векторам.
- •15. Система координат на прямой. Координата вектора прямой. Координата точки прямой.
- •16°. Аффинная ск на плоскости. Координаты вектора на плоскости. Координаты точки на пл. Прямоугольная ск на пл.
- •17. Аффинная cк в пространстве. Координаты вектора в простр. Координаты точки в простр. Прямоугольная ск в простр.
- •18°. Свойства линейных операций над векторами в координатной форме.
- •20. Преобразование прямоугольных координат.
- •19. Полярная, цилиндрическая и сферическая системы координат.
- •21°. Скалярное произведение векторов. Свойства скалярного произведения векторов.
- •22. Выражение скалярного произведения векторов, заданных прямоугольными координатами.
- •23°. Векторное произведение векторов. Свойства векторного произведения векторов.
- •24. Выражение векторного произведения векторов, заданных прямоугольными координатами.
- •25°. Смешанное произведение векторов. Теорема о вычислении объема параллелепипеда, построенного на трех векторах.
- •26. Выражение смешанного произведения векторов, заданных прямоугольными координатами.
- •27°. Уравнение прямой на плоскости, проходящей через данную точку в данном направлении (каноническое уравнение прямой).
- •28. Общее уравнение прямой на плоскости.Параметрическое уравнение прямой на плоскости.
- •37°. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой. Уравнение плоскости в отрезках.
- •38.Частные случаи расположения плоскости относительно ск.
- •39°. Уравнение прямой в пространстве, проходящей через данную точку в данном направлении (каноническое уравнение прямой).
- •40°. Параметрическое уравнение прямой в пространстве.
- •41°. Уравнение прямой в пространстве, проходящей через две точки.
- •52. Исследование формы эллипса
- •53. Гипербола и ее каноническое уравнение
- •54. Исследование формы гиперболы
- •55. Директрисы эллипса и гиперболы
- •56. Парабола и ее каноническое уравнение
- •57.Исследование формы параболы
- •58. Плоские фигуры n-порядка заданные общим уравнением.
- •59◦.Эллиспоид
- •60. Исследование формы эллипсоида методом сечений.
- •61°. Однополостный и двуполостный гиперболоиды.
- •62. Исследование формы гиперболоидов методом сечений.
- •63°. Конус второго порядка.
- •65°. Эллиптический и гиперболический параболоиды.
- •67. Цилиндры второго порядка. Эллиптический, гиперболический и параболический цилиндры.
- •68. Поверхности второго порядка, заданные общим уравнением.
- •69. Бинарные отношения.
- •70°. Отношение эквивалентности и порядка.
- •71°. Алгебраическая операция. Свойства алгебраических операций.
- •72°.Определение группы.Простейшие свойства групп.
- •73°. Определение кольца. Простейшие свойства колец.
- •74°.Определение поля.Простейшие свойства поля.
- •75.Изоморфизмы групп, колец.
- •76⁰.Построение поля комплексных чисел.Алгебраическая форма комплексного числа.
- •77°.Тригонометрическая и экспоненциальная форма записи комплексного числа.Действия над компл. Числами в триг.И экспон.Форме записи.
- •79.Корни n-ой степени из единицы
- •80. Кольцо многочлена от одной переменной
- •81°. Теорема о делении с остатком в кольце многочленов.
- •82. Наибольший общий делитель многочленов. Взаимно простые многочлены. Алгоритм Евклида.
- •83. Разложение многочлена на неприводимые многочлены.
- •84°. Корни многочлена от одной переменной. Схема Горнера.
- •85. Интерполяционный многочлен Лагранжа.
- •86. Рациональные дроби. Разложение правильной рациональной дроби в сумму простейших дробей.
- •87°. Многочлены с рациональными коэфициентами. Нахождение корней многочленов с рациональными коэфициентами.
- •88. Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна.
12. Понятие линейной зависимости векторов. Линейно независимые векторы. Необходимое и достаточное условие коллинеарности двух векторов. Необходимое и достаточное условие компланарности трех векторов.
Говорят,
что векторы
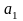 ,
,
 ,
,
 ,
,
 линейно зависимы, если существуют числа
линейно зависимы, если существуют числа
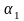 ,
,
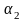 ,
,
,
,
 ,
не все равные нулю и такие, что линейная
комбинация
,
не все равные нулю и такие, что линейная
комбинация
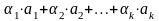 равна нулевому элементу
равна нулевому элементу
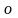 линейного пространства
линейного пространства
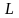 .
.
Если
же равенство
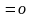 возможно только при условии
возможно только при условии
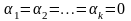 ,
то векторы
,
,
,
называют линейно независимыми.
,
то векторы
,
,
,
называют линейно независимыми.
Лемма. Векторы , , , линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся.
Необходимое и достаточное условие коллинеарности двух ненулевых векторов
Теорема. Для
того, чтобы два ненулевых вектора
 и
и
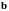 были коллинеарны, необходимо и достаточно,
чтобы их векторное произведение было
бы равно нулю.( a|
| b
a,b
- ЛЗВ )
были коллинеарны, необходимо и достаточно,
чтобы их векторное произведение было
бы равно нулю.( a|
| b
a,b
- ЛЗВ )
Доказательство.
Необходимость. Пусть
векторы
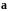 и
и
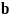 коллинеарны,
тогда они лежат на одной прямой,
следовательно,
коллинеарны,
тогда они лежат на одной прямой,
следовательно,
 =>
=>
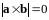 .
Значит,
.
Значит,
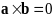
Достаточность.
Пусть векторное
произведение
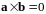 .
Так как
.
Так как
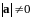 ,
,
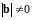 ,
то значит
,
то значит
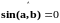 ,
т.е.
,
т.е.
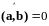 или
или
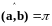 ,
а это означает, что векторы
и b
коллинеарны.
,
а это означает, что векторы
и b
коллинеарны.
Необходимое и достаточное условие компланарности трёх векторов
Теорема. Для того чтобы ненулевые векторы a,b и c были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.(a1, a2, a3 – комплонарны a1, a2, a3 - ЛЗВ)
Доказательство.
Необходимость.
Пусть векторы a,b,c
компланарны. Тогда их можно поместить
в одной плоскости, и вектор
 окажется перпендикулярным векторy
a,
следовательно, их скалярное произведение
равно нулю, т.е.
окажется перпендикулярным векторy
a,
следовательно, их скалярное произведение
равно нулю, т.е.
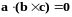 .
.
Достаточность.
Пусть
 .
Так как векторы ненулевые, то может
быть:
.
Так как векторы ненулевые, то может
быть:
1)
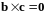 ,
тогда
,
тогда
 ,
следовательно, векторы a,b,c
можно поместить в одной плоскости, т.е.
они компланарны;
,
следовательно, векторы a,b,c
можно поместить в одной плоскости, т.е.
они компланарны;
2)
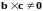 ,
но
,
но
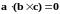 =>
=>
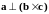 .
Это значит, что вектор a
лежит в одной плоскости с векторами b
и c.
.
Это значит, что вектор a
лежит в одной плоскости с векторами b
и c.
13°. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам.
Пусть дана π-плоскость , e1 ,e2 – ЛЗВ, тогда любой вектор а в плоскости π, можно представить в виде линейной комбинации:
a = xe1 +ye2 ,
причем данное представление единсивенное.
Пусть
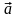 и
и
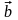 - данные неколлинеарные векторы. Докажем
сначала, что любой вектор
- данные неколлинеарные векторы. Докажем
сначала, что любой вектор
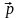 можно разложить по векторам
и
.
Возможны два случая.
можно разложить по векторам
и
.
Возможны два случая.
Вектор
коллинеарен одному из векторов
и
,
например вектору
.
В этом случае по лемме о коллинеарных
векторах вектор
можно представить в виде
 ,
где
,
где
 - некоторое число, и, следовательно,
- некоторое число, и, следовательно,
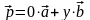 ,
т.е. вектор
разложен по векторам
и
.
,
т.е. вектор
разложен по векторам
и
.
Вектор
не коллинеарен ни вектору
,
ни вектору
.
Отметим какую-нибудь точку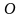 и отложим от нее векторы
и отложим от нее векторы
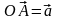 ,
,
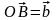 ,
,
 (рис.11). Через точку P
проведем прямую, параллельную прямой
(рис.11). Через точку P
проведем прямую, параллельную прямой
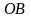 ,
и обозначим через A1
точку пересечения этой прямой с прямой
OA.
По правилу треугольника
,
и обозначим через A1
точку пересечения этой прямой с прямой
OA.
По правилу треугольника
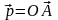 1
1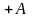 1
1 .
Но векторы
.
Но векторы
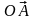 1
и
1
и
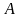 1
коллинеарны соответственно векторам
и
,
поэтому существуют числа
1
коллинеарны соответственно векторам
и
,
поэтому существуют числа
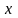 и
?
Такие, что
1=
и
?
Такие, что
1= ,A1
,A1
 .
Следовательно,
.
Следовательно,
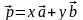 ,
т.е. вектор
,
т.е. вектор
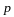 разложен по векторам
и
.
разложен по векторам
и
.
Д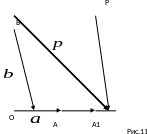 окажем
теперь, что коэффициенты
и
разложения определяются единственным
образом. Допустим, что наряду с разложением
имеем место другое разложение
окажем
теперь, что коэффициенты
и
разложения определяются единственным
образом. Допустим, что наряду с разложением
имеем место другое разложение
 х1
х1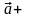 у1
.
Вычитая второе равенство из первого и
используя правила действий над векторами,
получаем
у1
.
Вычитая второе равенство из первого и
используя правила действий над векторами,
получаем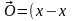 1)
1)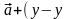 1).
Это равенство можно выполнять только
в том случае, когда коэффиценты
1).
Это равенство можно выполнять только
в том случае, когда коэффиценты
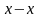 1
и
1
и
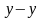 1
равны нулю. В самом деле, если предложить,
например, что х-х1
1
равны нулю. В самом деле, если предложить,
например, что х-х1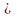 0,
то из полученного равенства найдем
0,
то из полученного равенства найдем
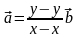 ,
а значит, векторы
и
коллинеарны. Но это противоречие условию
теоремы. Следовательно, х-х1=0
и у-у1=0,
откуда х=х1
и у=у1.
Это и означает, что коэффиценты разложения
вектора
определяются единственным образом.
,
а значит, векторы
и
коллинеарны. Но это противоречие условию
теоремы. Следовательно, х-х1=0
и у-у1=0,
откуда х=х1
и у=у1.
Это и означает, что коэффиценты разложения
вектора
определяются единственным образом.
