82. Наибольший общий делитель многочленов. Взаимно простые многочлены. Алгоритм Евклида.

Опр. Пусть f(x),g(x)ϵF[x] при чем степень многочлена deg f(x)≥ deg(x), f(x) g(x), если сущ. ϕ (x), это f(x)=g(x).

Св-ва.

, если r(x)=0

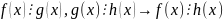
Опр. Многочлен кот.явл.делителем 2 других многочленов наз. Их общих делителем.

Опр. Наибольшим общим делителем f(x) и g(x) наз. Их общий делитель кот. Делится на все остальные их общие делители. Нод определен с точностью до числового множества. Нод(f(x),g(x))=d(x)

Опр. Многочлены наз. Взаимно простыми., если НОД их явл. Многоченом нулевой степени .

Теорема. Если f(x)=g(x)*q(x)+r(x), то НОД многочлен f(x),g(x), такой же НОД(g(x),f(x)).

АЛГОРИТМ ЕВКЛИДА

Найти НОД (f(x),g(x)). Пусть Deg f(x) ≥ deg g(x), если f(x) g(x), тогда НОД (f(x),g(x)) = g(x), если не так, то f(x)=g(x)*q(x)+r(x): многочлен.

g(x)=r₁(x)*q₂(x)+r₂(x), если r₂!=0, то

r₁(x)=r₂(x)*q₃(x)+r₃(x)…

r_n-1=r_n(x)*q_n+1(x)

теорема. Если d(x)=НОД(f(x),g(x))

Критерий взаимнопростые многочлены:f(x) и g(x)-взаимопростые

83. Разложение многочлена на неприводимые многочлены.

Пусть f(x) многочлен из F[x], F – поле, многочлен f(x) наз-ся неприводимым над полем F, если он не имеет делителей кроме делителей нулевой степени(α и αf(x)). В противоположном случае многочлен называется приводимым.

Св-ва неприводимого мн-чл.

1)Если f(x) – неприводим, а α – элемент поля, α!=0, то α(f(x)) - неприводим

2)Многочлен 1-ой степени над любым полем неприводим

3)Если f(x) – неприводим, g(x) – произвольный мн/чл., то либо g(x) f(x) или НОД (f(x),g(x))=1

ТЕОРЕМА

Всякий многочлен можно представить в виде произведения неприводимого многочлена, причем данное разложение единственно с точностью до числового множителя и порядка следования множителей.

84°. Корни многочлена от одной переменной. Схема Горнера.

Пусть F-поле, С-элемент поля, тогда F(C)= -значение многочлена при x=c.

ОПР.Элемент С взятый из поля F, называется корнем многочлена f(x) F[x], если f(C) = 0

Теорма Безу: Элемент С явл. Корнем f(x), тогда и тока тогда, когда

СХЕМА ГОРНЕРА пусть f(x)=a₀xⁿ + a₁x^n-1 +…+ a_n-1x + a_n; C F(элемент поля), f(x)=(x-c)*q(x)+r.

q(x)=b₀x^n-1 + b₁x^n-2 +…+ b_n-2x + b_n-1

	a0	a1	a2	…	an-1	an
C	b0	b1=a1+C*b0	b2=a2+C*b1	…	Bn-1=an-1+C*bn-2	r=an+C*bn-1

Опр. Пусть с-корень f(x). C-наз.K- Кратным корнем f(x), если , но не делится на .

Теорема.Многочлен в степени n имеет n-корень, при этом если многочлен разложен на первую степень, то он имеет n-четное кол-во корней.

85. Интерполяционный многочлен Лагранжа.

ТЕОРЕМА Для любого натур числа n существует единственный многочлен степени ≤n, который принимает на перед заданные значения для n+первого значения переменной

Д-ВО:

Пусть многочлен f(x)

	A0	…	An
F(x)	B0	…	Bn

f(a₀)=b₀ ,…, f(a_n)=b_n

f(x) = _{j j}(x)

. _j(x) = ;

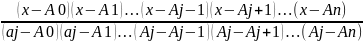f(a₀)= _{j j}(a₀) = b₀ (a_n) + b_{1 1}(a₀)