
- •1°. Понятие матрицы. Элементарные преобразования матрицы.
- •2. Ступенчатая матрица. Теорема о приведении матрицы к ступенчатой матрице.
- •3°. Системы линейных уравнений (слу). Решение слу. Эквивалентные слу. Однородные слу.
- •4. Метод Гаусса решения систем линейных уравнений.
- •5°. Определители второго и третьего порядков.
- •7. Миноры и их алгебраические дополнения. Теорема Лапласа.
- •8°. Обратная матрица.
- •9. Правило Крамера решения систем линейных уравнений.
- •10°. Направленный отрезок. Эквивалентные направленные отрезки. Понятие вектора. Угол между векторами. Коллинеарные и компланарные векторы.
- •11°. Операции над векторами. Свойства операции над векторами.
- •12. Понятие линейной зависимости векторов. Линейно независимые векторы. Необходимое и достаточное условие коллинеарности двух векторов. Необходимое и достаточное условие компланарности трех векторов.
- •13°. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам.
- •13. Теорема о разложении вектора на плоскости по двум неколлинеарным векторам.
- •14. Теорема о разложении вектора в пространстве по трем некомпланарным векторам.
- •15. Система координат на прямой. Координата вектора прямой. Координата точки прямой.
- •16°. Аффинная ск на плоскости. Координаты вектора на плоскости. Координаты точки на пл. Прямоугольная ск на пл.
- •17. Аффинная cк в пространстве. Координаты вектора в простр. Координаты точки в простр. Прямоугольная ск в простр.
- •18°. Свойства линейных операций над векторами в координатной форме.
- •20. Преобразование прямоугольных координат.
- •19. Полярная, цилиндрическая и сферическая системы координат.
- •21°. Скалярное произведение векторов. Свойства скалярного произведения векторов.
- •22. Выражение скалярного произведения векторов, заданных прямоугольными координатами.
- •23°. Векторное произведение векторов. Свойства векторного произведения векторов.
- •24. Выражение векторного произведения векторов, заданных прямоугольными координатами.
- •25°. Смешанное произведение векторов. Теорема о вычислении объема параллелепипеда, построенного на трех векторах.
- •26. Выражение смешанного произведения векторов, заданных прямоугольными координатами.
- •27°. Уравнение прямой на плоскости, проходящей через данную точку в данном направлении (каноническое уравнение прямой).
- •28. Общее уравнение прямой на плоскости.Параметрическое уравнение прямой на плоскости.
- •37°. Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой. Уравнение плоскости в отрезках.
- •38.Частные случаи расположения плоскости относительно ск.
- •39°. Уравнение прямой в пространстве, проходящей через данную точку в данном направлении (каноническое уравнение прямой).
- •40°. Параметрическое уравнение прямой в пространстве.
- •41°. Уравнение прямой в пространстве, проходящей через две точки.
- •52. Исследование формы эллипса
- •53. Гипербола и ее каноническое уравнение
- •54. Исследование формы гиперболы
- •55. Директрисы эллипса и гиперболы
- •56. Парабола и ее каноническое уравнение
- •57.Исследование формы параболы
- •58. Плоские фигуры n-порядка заданные общим уравнением.
- •59◦.Эллиспоид
- •60. Исследование формы эллипсоида методом сечений.
- •61°. Однополостный и двуполостный гиперболоиды.
- •62. Исследование формы гиперболоидов методом сечений.
- •63°. Конус второго порядка.
- •65°. Эллиптический и гиперболический параболоиды.
- •67. Цилиндры второго порядка. Эллиптический, гиперболический и параболический цилиндры.
- •68. Поверхности второго порядка, заданные общим уравнением.
- •69. Бинарные отношения.
- •70°. Отношение эквивалентности и порядка.
- •71°. Алгебраическая операция. Свойства алгебраических операций.
- •72°.Определение группы.Простейшие свойства групп.
- •73°. Определение кольца. Простейшие свойства колец.
- •74°.Определение поля.Простейшие свойства поля.
- •75.Изоморфизмы групп, колец.
- •76⁰.Построение поля комплексных чисел.Алгебраическая форма комплексного числа.
- •77°.Тригонометрическая и экспоненциальная форма записи комплексного числа.Действия над компл. Числами в триг.И экспон.Форме записи.
- •79.Корни n-ой степени из единицы
- •80. Кольцо многочлена от одной переменной
- •81°. Теорема о делении с остатком в кольце многочленов.
- •82. Наибольший общий делитель многочленов. Взаимно простые многочлены. Алгоритм Евклида.
- •83. Разложение многочлена на неприводимые многочлены.
- •84°. Корни многочлена от одной переменной. Схема Горнера.
- •85. Интерполяционный многочлен Лагранжа.
- •86. Рациональные дроби. Разложение правильной рациональной дроби в сумму простейших дробей.
- •87°. Многочлены с рациональными коэфициентами. Нахождение корней многочленов с рациональными коэфициентами.
- •88. Неприводимые многочлены над полем рациональных чисел. Критерий Эйзенштейна.
76⁰.Построение поля комплексных чисел.Алгебраическая форма комплексного числа.
Пусть z1=a1+b1i, z2=a2+b2i принадлежат С, z1=z2,если a1=a2,b1=b2.
Опр.
Суммой двух элементов z1
и z2єС
наз.эл.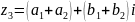 .
.
Опр.Произведением
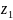 и
и
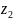 н.
н. .
.
Теорема. Множество С={a+bi|a,bєR} с операциями сложения и умн. явл-ся полем.Зам:каждый ненулевой элемент множества обратим.
Опр.
Пусть z=a+bi
є C
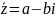 наз.комплексно-сопряж.
наз.комплексно-сопряж.
Опр. Пусть z=a+bi є C; a=Rez-действит. часть компл.числа;b=Imz-мнимая часть; a+0i – действительные числа; 0+bi – мнимые числа.
77°.Тригонометрическая и экспоненциальная форма записи комплексного числа.Действия над компл. Числами в триг.И экспон.Форме записи.
Рассм.С={a+bi|a,bєR} z=a+bi.Каждому числу z=a+bi можно поставить в соответствие точку с координатами (a,b)в прямоугольной CK.и наоборот –это взаимно однозначное соответствие.
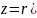 -
тригонометрическая форма записи
компл.числа.
-
тригонометрическая форма записи
компл.числа.
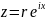 – экспоненциальная форма.
– экспоненциальная форма.
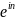 =-1.
=-1.
 =
=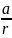 .
.
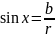 .
.
78°.Возведение в степень и извлечение корня n-ой степени из комплексного числа.
Опр.z0=1;z1=z;zn=z*z*z…
Опр.
Z-n=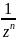 . Формула Муавра:
. Формула Муавра:
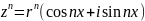 ;
Опр.Корнем
n-ой
степени из числа z
наз.число w
такое, что wn=z;Если
z=0,то
;
Опр.Корнем
n-ой
степени из числа z
наз.число w
такое, что wn=z;Если
z=0,то
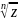 =0;если
z
0,то
z=a+bi=r(cosx
+isinx);
r(cosx+isinx)=r0n(cosnx0+isinnx0);
r0=
=0;если
z
0,то
z=a+bi=r(cosx
+isinx);
r(cosx+isinx)=r0n(cosnx0+isinnx0);
r0=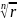 ;
w=
(
;
w=
( +i
+i
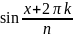 )
– корень n-ой
степени.
)
– корень n-ой
степени.
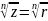 (
+i
)
(
+i
)
79.Корни n-ой степени из единицы
рассмотрим
z=1+0i
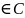
.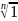
1+0i=r(cos ϕ +isin ϕ)
1+0i=1(cos 0 + i sin 0)
r=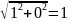 r=
r=
cos
ϕ=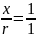 sin ϕ =
sin ϕ = ϕ=0;
ϕ=0;
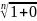 =
=
(cos
=
=
(cos
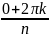 + I
)=1(
cos
+ I
)=1(
cos
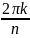 + i sin
),
k
+ i sin
),
k 0;n-1.
0;n-1.
= cos + I sin
Теорема.Множество всех комплексных корней n-ой степени из единицы образуют абелевую группу относительно умножения ( ,Ƹ0 ,Ƹ1 ,Ƹ2 ,…, Ƹn )
Ƹni=1 i=0;n-1
Ƹ0=Ƹ0
Ƹ1=Ƹ1
Ƹn=Ƹn
Ƹ – произвольный корень
Ƹ
= cos
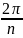 + i
sin
+ i
sin
80. Кольцо многочлена от одной переменной
Рассмотрим некоторое F-коммутативное кольцо с единицей.
F – Z,Q,C,R
ОПР. Многочленом(полиноном) от переменной х заданным над кольцом F, наз. выражение вида
a0+a1x+a2x2+…+anxn , ai F; i = 0;n, n – целое положительное
f(x)= a0+a1x+a2x2+…+anxn
Опр. если an !=0, an+1 = 0, an+2 = 0, то n = deg f(x), an – старший коэ-т, a0 – свободный коэ-т.
f(x)=0+0x+…+0xn – нулевой многочлен он не имеет степени
F[x] – множество всевозможных многочл.над кольцом F
Z[x] – целочисленный многочлен
На множестве F[x] введем 2 операции, умножение и сложение
F0(x), g(x) F[x]
f(x)= a0+a1x+ …+anxn
g(x)= b0+b1x +…+bkxk
f(x)+g(x) = C0+C1x+ …+Csxs , где s – максимум из n и k (C0=a0+b0,C1=a1+b1 …Ci=ai+bi)
f(x)*g(x)=d0+d1x+…+dmxm,
где m
- сумма k
и n;
di
=
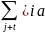 jbt
jbt
операция сложения – приведение подобных
операция умножения – раскрытие скобок, прив. подобных
deg(f(x) + g(x)) ≤ max {deg f(x), deg g(x)}
deg (f(x) * g(x))≤ deg f(x) * deg g(x)
ТЕОРЕМА. Множество F[x] является коммутативным кольцом с единицей относительно операции сложения и умножения многочленов
81°. Теорема о делении с остатком в кольце многочленов.
Теорема.пусть f(x) и g(x) – некоторые многочлены, тогда существуют многочлены q(x) и r(x) F[x], что f(x) = g(x)*q(x)+ r(x), r(x) степень меньше чем g(x) или r(x) = 0 данное представление единственно
Док-во: 1) deg f(x)<deg f(x), то f(x)=g(x)*0+f(x) 2) deg f(x)≥deg g(x)
f(x)=f(x)--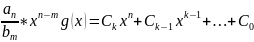 если m<n
если m<n
если
k<m,
то f(x)=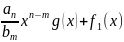
если
k≥m,
то
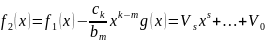 ,
где s<x
,
где s<x
продолжая аналогично. Мы найдем fi (x) степень которого меньше fi(x)=r(x).
Пусть
f(x)=g(x)*q(x)+r(x),
f1(x)=g(x)*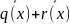 ;
;
f(x)-f1(x)=g(x)(
q(x)-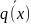 )+(
r(x)-
)+(
r(x)- )
)
g(x)( q(x)- )= -r(x)+
