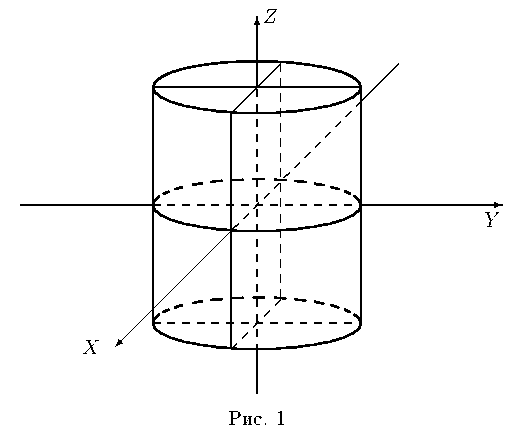
67. Цилиндры второго порядка. Эллиптический, гиперболический и параболический цилиндры.

Опр. Пусть π-некоторая плоскость, ϒ-некоторая линия этой плоскости через каждую точку линии ϒ проведем прямые перпендикулярно плоскости π. Образовавшейся поверхность наз. Цилиндрической.

Опр. Линия ϒ-явл. Фигурой 2 порядка, то цилиндрическая поверхность наз.цилиндром второго порядка.

Эллиптический цилиндр

Гиперболический цилиндр

Параболический цилиндр

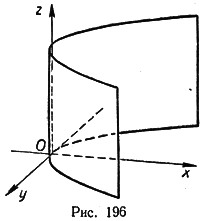
68. Поверхности второго порядка, заданные общим уравнением.

Опр. Уравнение вида

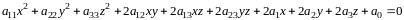, (2.1)

где , , , ,

(т.е. хотя бы один коэффициент ) называется уравнением второго порядка от трех переменных.

Опр. Фигура, которая в некоторой специально выбранной прямоугольной системе координат может быть задана уравнением (2.1) называется поверхностью второго порядка.

Пример. Пусть фигура задана уравнением . Здесь , , , , а все остальные коэффициенты равны нулю. Перейдем к новой системе координат по формулам:

(2.2)

Если (2.2) подставить в уравнение (2.1), и наложить условие, что коэффициенты при слагаемых , , будут равны нулю, то получим уравнение вида (2.3)

где , , находятся из уравнения:

,

а углы в системе (2.2) находятся из решения системы:

Рассмотрим случаи.

I) Пусть , , 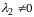. Тогда

, где .

Обозначая новую систему координат будем иметь , , . Теперь имеем

Возможны следующие случаи:

I₁. Если , , , D одного знака, то фигура, заданная уравнением (2.1) – эллипсоид.

I₂. Если , , одного знака, а D противоположного знака, то фигура, заданная уравнением (2.1) – пустое множество (мнимый эллипсоид).

I₃. Если , , одного знака, а противоположного знака, то фигура, заданная уравнением (2.1) – однополостный гиперболоид.

I₄. Если , одного знака, а , противоположного знака, то фигура, заданная уравнением (2.1) – двуполостный гиперболоид.

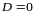I₅. Если , , одного знака, а , то фигура, заданная уравнением (2.1) – точка (начало координат, точка ).

I₆. Если , одного знака, противоположного, , то фигура, заданная уравнением (2.1) – конус.

69. Бинарные отношения.

Бинарным отношением, заданным на множестве А, называется подмножество R≤А²(А×А). Если a и b є А, то aRb(элемент а находится в бинарном отношении R с элем.b). Пусть на множ. А задано бин.отнош.R, тогда,если R=A²,то назыв. универ сальное бинарное отношение,если R=0,то R-пустое бин.отнош.Опр.Б.о.R назыв.

1) рефлексивным,если aRa;

2) симметричным,если aRb→bRa;

3) транзитивным,если aRb, bRc→aRc;

4) антисимметричным, если aRb, bRa→a=b.

70°. Отношение эквивалентности и порядка.

Отношение эквивалентности и порядка.Б.о.R наз.отношением эквивалентности,если R-рефлексивно,симметрично и транзитивно.

Опр.Пусть R-отнош.экв. аєА.Множество ā={xєA|aRx}назыв. классом эквивалентности элем. а. Теорема:любых два класса эквивалентности либо не пересекаются, либо совпадают.

Опред:если на множ.А задано отнош.эквив. ̴,то совокупность всевожможных непересекающихся классов эквив. наз. фактор-множеством(А ̰).Б.о. наз. отнош.частичного порядка,если рефл., антисимм., транзитивно.Элем. a и b-сравнимые,если aRb или bRa, в противном случае они несравнимы.