55. Директрисы эллипса и гиперболы

Опр: Директрисой эллипса (гиперболы) называется прямая перпендикулярная факальной оси и отстоящая от центра эллипса и гиперболы на расстояние a/ε

, a>b 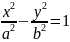, a>c

x=-1/ε x=1/ ε x=-a/ ε x=a/ ε

Теорема: Для всех точек эллипса (гиперболы) отношение расстояния до фокуса к расстоянию до соответствующей директрисы есть число постоянно равное эксцентриситету. Если есть точка и прямая, то все точки, для которых отношение расстояния до точки к расстоянию до прямой есть число постоянное, которые являются точками эллипса(гип. ε>1)

Доказательство:=>

MF₂ =r₂=a- εx

MK=a/ε-x

(a-εx)/(a/ε-x)= ε, ε>1 - гиперболаε<1-эллипс

56. Парабола и ее каноническое уравнение

Пусть на плоскости задана некоторая точка и прямая

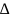
Опр: Параболой называется множество точек плоскости, для которых расстояние от точки F и данной прямой равны. F – фокус, а - директриса.

Введем прямоугольную систему координат ось Ox это прямая проходящая через FL (перпендикулярно), O начало координат и середина ОF. ρ(f, =p; F(p/2;0), x=-p/2-директриса.

Пусть М-произвольная точка, тогда M(x, y); MF=ρ(M, )

MF=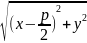 ρ(M, )=x+p/2

=x+p/2

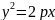– каноническое уравнение параболы.

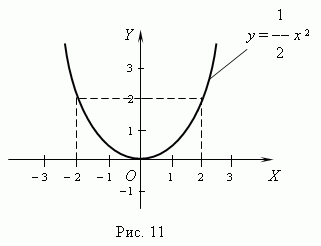
57.Исследование формы параболы

Пусть у²=2рх – каноническое уравнение параболы в специально выбранной системе координат.

Чем больше р , то больше расходятся ветви и наоборот.

Т.к. р>0, y²≥0, то x≥0.

Если точка M₁(x₁, y₁) принадлежит параболе, то точка M₂(x₁ , -y₁) принадлежит параболе, парабола симметрично оси Ох.

X≥0, y≥0 y=

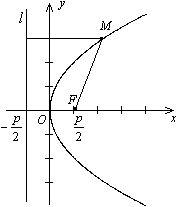
Если х=0, то у=0

О(0, 0)- вершина параболы.

Если х возрастает, то

у возрастатет.

Опр. Факальной осью

параболы называется

прямая , проходящая

через фокус перпендикулярно директрисе.

Опр. факальный параметр= р

Примеры:

1)у²=-2рх – неканоническое уравнение параболы х^’=y, y^’=x.F(-p/2, 0)

Ветви параболы наклонены по оси О_х во II-ой и III –ей четверти.

2)х²=2ру у=-р/2 у=у^’ ; F(0, p/2)

Ветви параболы наклонены по оси O_y в I – ой и II-ой четвертях

3)х²=-ру х^’=-y, y^’=x; y=p/2 F(0, -p/2)

Ветви параболы наклонены по оси О_уIII-ей и IV-ой четвертях .

58. Плоские фигуры n-порядка заданные общим уравнением.

Опр. Уравнение вида 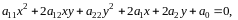(2.1) где 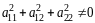, называется уравнением второго порядка от двух переменных и .

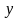Определение. Фигуры плоскости, которые могут быть заданы уравнением вида (2.1) называют плоскими фигурами второго порядка.

Пусть 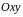– старая система координат, 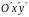– новая система координат.

Пусть в (2.1) 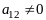, тогда .

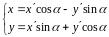Подставим новые значения 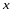и в (2.1), имеем:

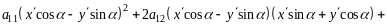
Откуда имеем, ,

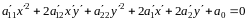Где

Условие имеет вид 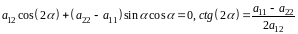(2.2). При повороте системы координат на угол из (2.2) уравнение (2.1) примет вид

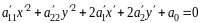
(коэффициент ).

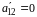59◦.Эллиспоид

Опр. Эллисоид назыв.фигура которая в некоторой специально выбранной прямоугольной системе координат может быть заданна ур-ние 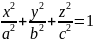, где (a,b,c>0,ϵR).

Если а=b=c ,то уравнение x²+y²+z²=a² определяет сферу радиуса а.

В силу того, что x,y,z входят в ур-ние в четной степени, то эллипсоид симметричен относительно начало координат, координатных плоскостей и координатных осей. Начало координат назыв. Центром эллипсоидом О(0,0,0) оси Ox,Oy,Oz назыв. Главной осью. Точки пересечения с главными осями наз. Вершинами эллипсоидом. А₁(-a,0,0); A₂(a,0,0); B₁(0,-b,0); B₂(0,b,0); C₁(0,0,-c); C₂(0,0,c).

|x|≤a, |y|≤b, |z|≤c. В связи с этим все точки эллипсоида находятся внутри параллепипеда.

x=a, x=-a; y=b, y=-b; z=c, z=-c;

Если b=c, то ур-ние 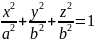(эллипсоид вращения, кот. получается вращением факальной плоскости)