40. Разложение нормального потенциала в ряд сферических функций.
Нормальный потенциал описывается выражением:
(1)
Где GM=G ( МЗемли + Матмосферы) – геоцентрическая гравитационная постоянная, учитывающая атмосферу Земли, а – большая полуось общеземного эллипсоида.
Присоединенные функции Лежандра Pl,m степени l и порядка m выражаются через аргумент t в виде:
Pl,m
(t) =
для полиномов Лежандра (m=0)
Если
l=0,
1, 2, то при t=cos
имеем
Р0=1, Р1=cos , P1,1=sin ,
Р2=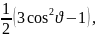
Р2,2= 3
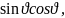Р2,2=3
.
Поверхностные сферические функции Лапласа
Pl,m
(
)
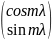
описывают
в формуле (1) потенциал на сфере единичного
радиуса. Нулевые значения этих функций
разделяют поверхность сферы на участки,
где функции имеют разные знаки. Участки
эти ограничены сеткой меридианов и
параллелей. Таким образом, разложение
в ряд по сферическим функциям представляет
собой спектральное разложение структуры
гравитационного поля по волнам длиной
в 360
/l.
Полиномы Лежандра описывают осесимметричное
поле, разделяя сферу на широтные зоны
(пояса); при четных значениях l
зоны симметричны относительно экватора.
Член нулевой степени соответствует
потенциалу однородной или состоящей
из концентрических сферических слоев
Земли. Если начало системы координат
совпадает с центром масс Земли, то члены
первой степени отсутствуют.
Обычно для описания силы тяжести используют нормированные сферические гармоники, среднее квадратическое значение которых по всей сфере равно единице. Нормированные полиномы Лежандра находят из выражения
Pl,m(cos
)
Нормированные коэффициенты сферических функций Cl,m и Sl,mпредставляют собой интегралы по массе
Где k=1 при m=0 и k=2 при m≠0;
41. Фундаментальные постоянные.
*Из учебника Огородовой, стр. 210-211, совпадает с соответствующим материалом из лекций(только там 4 предложения).
При подборе уровенного эллипсоида в качестве нормальной Земли следует соблюдать следующие условия:
Центр уровенного эллипсоида совпадает с центром масс Земли, а его главная ось инерции с осью вращения Земли;
Уровенный эллипсоид вращается с той же угловой скоростью w, что и реальная Земля;
Масса уровенного эллипсоида равна массе реальной Земли fMэл=fM;
Зональные гармонические коэффициенты второй степени для уровенного эллипсоида и реальной Земли должны совпадать
Нормальный потенциал Uo силы тяжести на поверхности уровенного эллипсоида должен быть равен реальному потенциалу Wo СТ на уровенной поверхности, проходящей через исходный пункт нивелирования.
В пятом условии предпочтительнее брать большую полуось ур. эллип. и значит:
5)Большая полуось эллипсоида должна быть подобрана таким образом, чтобы его объем равнялся объему, охватываемому геоидом.
За фундаментальные геод. постоянные, характеризующие НЗ, в настоящее время приняты следующие величины: большая полуось эллипсоида а, геоцентрическая гравитационная постоянная fM, зональный коэфф. J2, угловая скорость вращения Земли.
