8. Проводники в электрическом поле. Равновесное распределение зарядов в проводнике. Ёмкость проводника. Конденсаторы. Соединение конденсаторов.

Проводник — среда, которая способна передавать заряд другим средам. Опыт показывает, что, если во внешнее электростатическое поле внести кусок проводника, то на одном конце сосредотачивается положительный заряд, а на другом отрицательный. То есть в проводнике должны находиться свободные электрические заряды. Такими зарядами являются электроны.

Рассмотрим заряженный проводник, находящийся в состоянии равновесия. Так как проводник находится в состоянии равновесия, то электростатические силы внутри проводника отсутствуют.

Для любой замкнутой поверхности внутри проводника:

Заряды будут стремиться на поверхность, при этом будут скапливаться с поверхностной плотностью . Значит, поверхность проводника стала эквипотенциальной, следовательно, вектор напряжённости на каждой точке этой поверхности перпендикулярен ей.

Так как , то (нормальная составляющая) и (тангенциальная составляющая). По выводам из раздела «поле заряженной поверхности»:

Где — напряжённость над поверхностью, — напряжённость под поверхностью. Так как , то

Результирующее поле определяется только нормальной составляющей.

Если напряжённость поля внутри проводника равна нулю, то (связь потенциала с напряжённостью). То есть везде в проводнике, и потенциал можно принять за характеристику проводника (только если он уединён). Если проводник не уединён, то на другом проводнике образуются свои заряды и создадут электростатическое поле.

Ёмкость

Рассмотрим уединённый проводник. Сообщим ему заряд и определим потенциал поля, создаваемым им относительно бесконечности.

Где — поверхность проводника. Теперь сообщим проводнику заряд , где . При этом . Определим потенциал поля относительно бесконечности.

Таким образом . Величина называется электроёмкостью проводника. Электроёмкость характеризует величину заряда, которую нужно сообщить проводнику, чтобы его потенциал стал равен единице. Определим размерность электроёмкости:

• СИ: (фарада) — ёмкость проводника, которому нужно сообщить заряд в 1Кл, чтобы его потенциал стал равен 1В.

• Сгс:

Ёмкость конденсаторов

Шар с радиусом :

Плоский конденсатор с площадью поверхности и расстоянием между пластинами :

Шаровой конденсатор:

Цилиндрический конденсатор:

Соединение конденсаторов

• При последовательно соединении

• При параллельном соединении

9. Диэлектрики в электрическом поле. Поляризация 2-х типов диэлектриков. Вектор поляризации. Поле в диэлектриках.

Диэлектрик — такая среда, которая не может передать свой заряд другой среде. Задача заключается в том, чтобы определить напряжённость внутри диэлектрика. Рассматриваются диэлектрики двух типов:

1. Неполярные. У таких диэлектриков центры положительного и отрицательного заряда в молекуле совпадают. , где — дипольный момент молекулы.

2. Полярные. У таких диэлектриков центры положительного и отрицательного заряда в молекуле не совпадают. , где — ось (расстояние между центрами зарядов) молекулы.

Неполярные диэлектрики

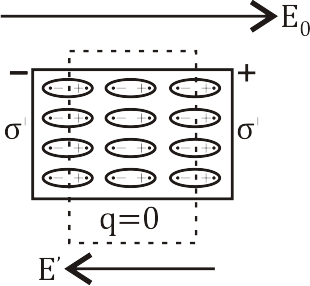— суммарный вектор напряжённости в диэлектрике.

Под действием внешнего электростатического поля молекулы «вытягиваются» и тем самым поляризуются. Поляризация — процесс деформации молекул, приводящий к образованию диполя. При этом молекула рассматривается как упругое тело. — коэффициент упругости.

Величина — поляризуемость молекулы диэлектрика.

— удельная величина дипольного момента (вектор поляризации). — концентрация (число молекул в единице объёма).

Величина — поляризуемость единицы объёма (восприимчивость диэлектрика).

и зависят от природы диэлектрика и не зависят от температуры.

Полярные диэлектрики

В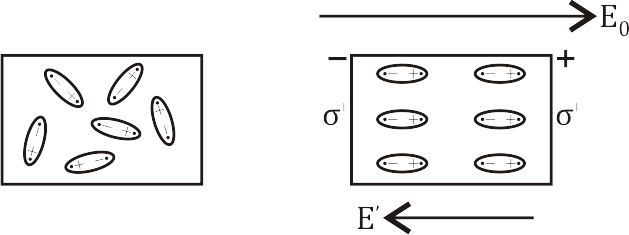 полярных диэлектриках наблюдается ориентационная поляризация, поэтому зависит от температуры.

Далее идёт общее рассуждение для обоих типов поляризации

Суммарный вектор напряжённости внутри диэлектрика определяется как сумма внешней напряжённости с напряжённостью, создаваемой поляризованными молекулами диэлектрика :

На поверхностях диэлектрика образуются противоположные заряды, поэтому можно рассматривать его как конденсатор с площадью поверхностей , зарядом на поверхностями , поверхностной плотностью заряда и расстоянием между пластинами .

Посчитаем величину вектора поляризации всех молекул:

Теперь можно найти :

— диэлектрическая проницаемость среды