
- •Предисловие
- •Электростатика
- •1. Предмет и задачи курса электромагнетизма (элм). Роль элм взаимодействий в природе. Понятие заряда, его свойства. Взаимодействие зарядов. Закон Кулона.
- •2. Электрическое поле в вакууме. Напряжённость поля. Принцип суперпозиции. Поле диполя (расчёт).
- •4. Работа по перемещению заряда в электрическом поле. Потенциальный характер электростатического поля. Теорема о циркуляции.
- •5. Дифференциальная форма потенциальности электростатического поля.
- •6.Электрическое поле заряженной поверхности.
- •7. Понятие потенциала. Нормировка потенциала. Потенциал поля точечного заряда. Разность потенциалов. Связь разности потенциалов и напряжённости поля. Понятие эквипотенциальной поверхности.
- •8. Проводники в электрическом поле. Равновесное распределение зарядов в проводнике. Ёмкость проводника. Конденсаторы. Соединение конденсаторов.
- •9. Диэлектрики в электрическом поле. Поляризация 2-х типов диэлектриков. Вектор поляризации. Поле в диэлектриках.
- •10. Теорема Гаусса в диэлектриках. Сегментоэлектрики. Пьезоэффект.
- •11. Энергия взаимодействия электрических зарядов. Собственная энергия заряда. Энергия электрического поля. Элементы термодинамики электрического поля.
- •12. Постоянный электрический ток. Основные характеристики поля постоянного тока. Теорема о непрерывности линий тока. Закон Ома в дифференциальной форме.
- •13. Интегральная форма закона Ома. Сторонние силы. Эдс. Правила Кирхгофа.
- •14. Работа и мощность тока. Закон Джоуля–Ленца. Кпд источника тока.
- •15. Проводимость в металлах. Опыты Толмена и Стюарта. Классическая теория проводимости твёрдых тел (Лоренца–Друдэ) и её затруднения.
- •21. Стационарное магнитное поле в вакууме. Закон Био–Савара–Лапласа. Расчёт магнитного поля прямого тока, кругового тока.
- •23. Силы, действующие на токи в магнитном поле. Магнитный момент рамки с током. Сила Лоренца.
- •24. Свойства магнитного поля. Теорема Гаусса и о циркуляции в магнитном поле. Понятие монополя.
- •25. Эффект Холла.
- •26. Теория магнетиков. Магнитный момент атомов. Прецессия Лармора. Природа диа-, парамагнетизма. Опыты Эйнштейна–де-Хааза, Бернста.
- •27. Классическая теория поля в магнетиках: вектор намагничивания, магнитная восприимчивость, молекулярные токи. Магнитное поле в магнетиках. Теорема Гаусса и о циркуляции в магнетиках.
- •28. Классификация магнетиков. Ферромагнетики. Квантовая теория ферромагнетизма.
- •Квазистационарные электрические и магнитные поля
- •29. Квазистационарное магнитное поле. Явление электромагнитной индукции. Закон Фарадея. Объяснение опытов Фарадея. 1-я гипотеза Максвелла. Явления само- и взаимоиндукции. Бетатрон (принцип действия).
- •30. Квазистационарные токи. Получение такого тока. Цепь переменного тока с индуктивностью. Метод векторных диаграмм. Импеданс. Закон Ома для такой цепи.
- •31. Энергия магнитного поля. Плотность энергии магнитного поля.
- •3 3. Цепь переменного тока с ёмкостью. 2-я гипотеза Максвелла. Ток смещения. Уравнение полных токов.
- •34. Цепь переменного тока, содержащая r, l и с. Закон Ома в цепи переменного тока. Импеданс. Резонанс токов и напряжений в цепи переменного тока.
- •35. Электромагнитное поле. Уравнения Максвелла.
- •36. Электромагнитные волны. Свободные электромагнитные волны. Поперечность электромагнитных волн. Скорость распространения электромагнитных волн. Софазность.
- •38. Энергия электромагнитных волн. Вектор Умова–Пойтинга. Диаграмма направленности излучения диполя.
Оглавление
Предисловие 3
Электростатика 4
1. Предмет и задачи курса электромагнетизма (ЭЛМ). Роль ЭЛМ взаимодействий в природе. Понятие заряда, его свойства. Взаимодействие зарядов. Закон Кулона. 4
2. Электрическое поле в вакууме. Напряжённость поля. Принцип суперпозиции. Поле диполя (расчёт). 5
3. Понятие силовой линии. Поток вектора напряжённости. Теорема Остроградского–Гаусса в интегральной и дифференциальной формах. Электрические заряды как источники и стоки электрического поля. Применение теоремы для расчёта электрических полей. 6
4. Работа по перемещению заряда в электрическом поле. Потенциальный характер электростатического поля. Теорема о циркуляции. 8
5. Дифференциальная форма потенциальности электростатического поля. 9
6.Электрическое поле заряженной поверхности. 9
7. Понятие потенциала. Нормировка потенциала. Потенциал поля точечного заряда. Разность потенциалов. Связь разности потенциалов и напряжённости поля. Понятие эквипотенциальной поверхности. 10
8. Проводники в электрическом поле. Равновесное распределение зарядов в проводнике. Ёмкость проводника. Конденсаторы. Соединение конденсаторов. 12
9. Диэлектрики в электрическом поле. Поляризация 2-х типов диэлектриков. Вектор поляризации. Поле в диэлектриках. 14
10. Теорема Гаусса в диэлектриках. Сегментоэлектрики. Пьезоэффект. 15
11. Энергия взаимодействия электрических зарядов. Собственная энергия заряда. Энергия электрического поля. Элементы термодинамики электрического поля. 17
Ток 19
12. Постоянный электрический ток. Основные характеристики поля постоянного тока. Теорема о непрерывности линий тока. Закон Ома в дифференциальной форме. 19
13. Интегральная форма закона Ома. Сторонние силы. ЭДС. Правила Кирхгофа. 20
14. Работа и мощность тока. Закон Джоуля–Ленца. КПД источника тока. 22
15. Проводимость в металлах. Опыты Толмена и Стюарта. Классическая теория проводимости твёрдых тел (Лоренца–Друдэ) и её затруднения. 22
16. Элементы квантовой теории проводимости тел. Сверхпроводимость. (БКШ и высокотемпературная сверхпроводимость). 24
17. Зонная теория проводимости тел. Проводимость проводников, полупроводников, диэлектриков. 24
18. Примесная проводимость полупроводников. Явления на границах полупроводников. Полупроводниковый диод, триод. 24
Магнетизм 25
20. Взаимодействие элементов тока в вакууме. Закон Ампера. 25
21. Стационарное магнитное поле в вакууме. Закон Био–Савара–Лапласа. Расчёт магнитного поля прямого тока, кругового тока. 26
23. Силы, действующие на токи в магнитном поле. Магнитный момент рамки с током. Сила Лоренца. 27
24. Свойства магнитного поля. Теорема Гаусса и о циркуляции в магнитном поле. Понятие монополя. 28
25. Эффект Холла. 29
26. Теория магнетиков. Магнитный момент атомов. Прецессия Лармора. Природа диа-, парамагнетизма. Опыты Эйнштейна–де-Хааза, Бернста. 29
27. Классическая теория поля в магнетиках: вектор намагничивания, магнитная восприимчивость, молекулярные токи. Магнитное поле в магнетиках. Теорема Гаусса и о циркуляции в магнетиках. 31
28. Классификация магнетиков. Ферромагнетики. Квантовая теория ферромагнетизма. 33
Квазистационарные электрические и магнитные поля 34
29. Квазистационарное магнитное поле. Явление электромагнитной индукции. Закон Фарадея. Объяснение опытов Фарадея. 1-я гипотеза Максвелла. Явления само- и взаимоиндукции. Бетатрон (принцип действия). 34
30. Квазистационарные токи. Получение такого тока. Цепь переменного тока с индуктивностью. Метод векторных диаграмм. Импеданс. Закон Ома для такой цепи. 35
31. Энергия магнитного поля. Плотность энергии магнитного поля. 38
33. Цепь переменного тока с ёмкостью. 2-я гипотеза Максвелла. Ток смещения. Уравнение полных токов. 39
34. Цепь переменного тока, содержащая R, L и С. Закон Ома в цепи переменного тока. Импеданс. Резонанс токов и напряжений в цепи переменного тока. 41
35. Электромагнитное поле. Уравнения Максвелла. 42
36. Электромагнитные волны. Свободные электромагнитные волны. Поперечность электромагнитных волн. Скорость распространения электромагнитных волн. Софазность. 43
38. Энергия электромагнитных волн. Вектор Умова–Пойтинга. Диаграмма направленности излучения диполя. 47
Конец 48
Предисловие
Эту «методичку» я составил в далёком 2012-м году по лекциям Полищук Раисы Фёдоровной для курса «электричество и магнетизм». Некоторых вопросов здесь нет (они помечены красным): одни она просто пропустила, на другие я внятного ответа найти не смог. Помни, пожалуйста, что я не несу ответственности за проблемы, связанные с тем, что тебе на контрольной или экзамене попался вопрос, которого здесь нет. Я старался максимально понятно и удобно изложить материал курса, хоть я и делал эту методичку в первую очередь для себя. Надеюсь, для тебя она тоже окажется полезной. Удачного изучения :).
Электростатика
1. Предмет и задачи курса электромагнетизма (элм). Роль элм взаимодействий в природе. Понятие заряда, его свойства. Взаимодействие зарядов. Закон Кулона.
Электродинамика изучает электрические заряды, их взаимодействие и поля, ими порождаемые и действующие на них.
В природе: явление электричества играет большую роль для процессов в нервной системе человека и животных (передача нервных импульсов).
Электрический заряд — физическая величина, принятая за меру заряженности тела, оцениваемая по способности электрического взаимодействия.
Точечный заряд — любое заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями.
Свойства заряда:
Квантованность. Заряд любого тела носит дискретный характер. Элементарные единицы: заряд протона и заряд электрона.

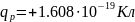


Аддитивность. Независимое алгебраическое сложение электрических зарядов.
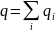
Инвариантность. Величина заряда не зависит от системы отчёта и от скорости движения.
Подчинение закону сохранения электрических зарядов. В замкнутой системе, несмотря на любые взаимопревращения, суммарная величина заряда остаётся постоянной.

Взаимодействие зарядов.
Разноимённые заряды притягиваются, одноимённые отталкиваются. Опыт показывают, что силы взаимодействия зависят от:
Величин зарядов.

Расстояния.

Размера заряда, формы и ориентации.
Силы
взаимодействия между зарядами подчиняются
принципу суперпозиции.
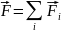
Взаимодействие между двумя зарядами не зависит от наличия других зарядов в пространстве.
З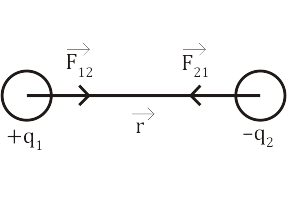 акон
кулона. Сила взаимодействия между
двумя точечными зарядами пропорциональна
их зарядам, обратнопропорциональна
квадрату расстояния между ними и носит
центральный характер.
акон
кулона. Сила взаимодействия между
двумя точечными зарядами пропорциональна
их зарядам, обратнопропорциональна
квадрату расстояния между ними и носит
центральный характер.
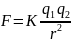


Где
 — коэффициент пропорциональности.
Определим размерность
— коэффициент пропорциональности.
Определим размерность
 :
:
Система СГС (грамм, сантиметр, секунда).
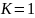


 — значение зарядов на расстоянии 1см,
при котором сила взаимодействия между
зарядами равна 1 дине.
— значение зарядов на расстоянии 1см,
при котором сила взаимодействия между
зарядами равна 1 дине.Система СИ (килограмм, метр, секунда, ампер).


 — такой заряд, который, проходя через
проводник за 1 секунду, вызывает ток в
1 ампер.
— такой заряд, который, проходя через
проводник за 1 секунду, вызывает ток в
1 ампер.
 Где
Где
 — диэлектрическая проницаемость
вакуума.
— диэлектрическая проницаемость
вакуума.

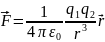
Закон
Кулона работает только в диапазоне
 –
– м.
м.
2. Электрическое поле в вакууме. Напряжённость поля. Принцип суперпозиции. Поле диполя (расчёт).
П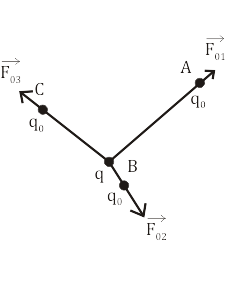 робный
заряд — заряд, служащий для обнаружения
других зарядов.
робный
заряд — заряд, служащий для обнаружения
других зарядов.
Электрическое поле — область пространства, которая изменяет физические свойства при наличии в ней зарядов, и которая воздействует на любой другой заряд, вносимый в эту область.
Так как заряд неподвижен, то это поле называется электростатическим полем.
Разделим закон Кулона на две части:
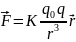
 и
и

Где
 — пробный заряд,
— пробный заряд,
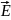 — напряжённость электростатического
поля,
— напряжённость электростатического
поля,
 — сила, действующая со стороны поля на
пробный заряд, помещённый в данную точку
поля.
— сила, действующая со стороны поля на
пробный заряд, помещённый в данную точку
поля.

Система СИ.
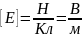
Система СГС.

Принцип суперпозиции полей выполняется только в линейных средах.
 Линейная
среда — среда, в которой отсутствуют
сегментоэлектрики и ферромагнетики.
Для нелинейных сред
Линейная
среда — среда, в которой отсутствуют
сегментоэлектрики и ферромагнетики.
Для нелинейных сред
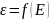 .
.

Где
 — объём тела,
— объём тела,
 — объёмная плотность заряда.
— объёмная плотность заряда.
Поле диполя.
Диполь — система из двух точечных электрических зарядов, равных по величине, но обратных по направлению.
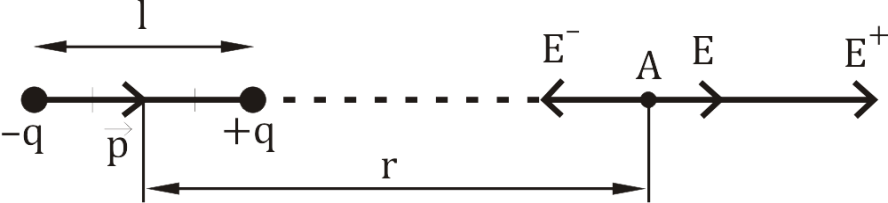
Элементарный
диполь:
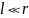 .
.
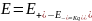
Так
как
,
то
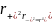

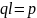 — величина дипольного момента.
— величина дипольного момента.
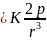
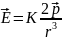
Для произвольной точки:

3. Понятие силовой линии. Поток вектора напряжённости. Теорема Остроградского–Гаусса в интегральной и дифференциальной формах. Электрические заряды как источники и стоки электрического поля. Применение теоремы для расчёта электрических полей.
Г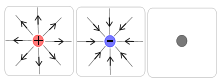 рафически
поле можно изобразить с помощью силовых
линий. Силовая линия — такая линия,
касательная к которой в любой её точке
совпадает по направлению с вектором
напряжённости поля. Принято проводить
густоту линий таким образом, чтобы через
единичную площадку
рафически
поле можно изобразить с помощью силовых
линий. Силовая линия — такая линия,
касательная к которой в любой её точке
совпадает по направлению с вектором
напряжённости поля. Принято проводить
густоту линий таким образом, чтобы через
единичную площадку
 проходило
проходило
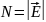 линий.
линий.
Силовые линии обладают следующими свойствами:
Через каждую точку поля можно провести одну линию.
Силовые линии начинаются или заканчиваются на зарядах, уходя в бесконечность.
В поле не может быть замкнутых силовых линий.
Если
имеется поле вектора напряжённости
 ,
то выражение
,
то выражение
 ,
где
,
где
 — составляющая вектора
по направлению нормали к
— составляющая вектора
по направлению нормали к
 ,
называется потоком вектора напряжённости
через поверхность
,
называется потоком вектора напряжённости
через поверхность
 .
.
Теорема Остроградского–Гаусса.
Покажем,
что окружающую точечный заряд
сферическая поверхность любого радиуса
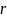 пересекает
пересекает
 линий
:
линий
:

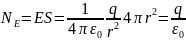
Для сферы:


Покажем, что и для любой другой поверхности это так:
Д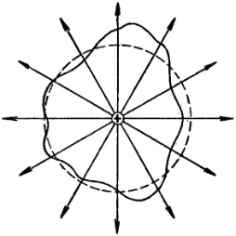
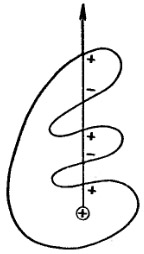 ля
поверхности, не имеющей «морщин», это
утверждение является очевидным, потому
что такая поверхность пересекается
каждой силовой линией только один раз.
ля
поверхности, не имеющей «морщин», это
утверждение является очевидным, потому
что такая поверхность пересекается
каждой силовой линией только один раз.
Силовая линия пересекает «морщинистую» поверхность всегда нечётное количество раз, поэтому общий поток всегда будет равен либо +1, либо –1 в зависимости от знака заряда.
Пусть
внутри замкнутой поверхности расположено
несколько точечных зарядов. В силу
принципа суперпозиции полей ( )
и
)
и
 :
:

Так
как
 ,
то
,
то

Это и есть теорема Остроградского–Гаусса. Если заряд распределён внутри замкнутой поверхности непрерывно с объёмной плотностью , теорема Остроградского–Гаусса может быть записана в интегральном виде:

Д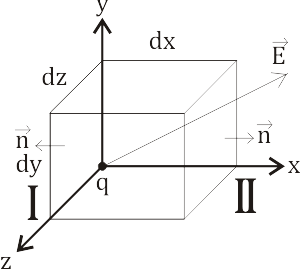 ля
того чтобы получить дифференциальную
форму, стянем поверхность
,
окружающую заряд, до бесконечно малой.
ля
того чтобы получить дифференциальную
форму, стянем поверхность
,
окружающую заряд, до бесконечно малой.
Рассмотрим поток вектора напряжённости, проходящий через поверхности I и II.
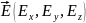

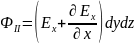

Аналогично получаем поток вектора напряжённости, проходящий через остальные поверхности:
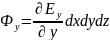

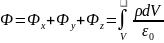

 — дивергенция
— дивергенция

Мы получили дифференциальную форму теоремы Остроградского–Гаусса.
