4.2Пример использования

По формуле (2.2.1) момент инерции равен . Для расчетов коэффициент пропорциональности между силой сопротивления воздуха и квадратом скорости квадрокоптера был принят равным .

Шаг интегрирования в основной программе был принят равным , шаг интегрирования в блоке вычисления текущего значения силы тяги .

Экспериментально были получены константы , , и .

Таблица1. Константы

Физические величины			Коэффициенты алгоритма
, кг2 1
, кг0,07 1,5
	0,7			9
	0,0523			2,5
	0,1

Пример 1

В данном случае в начальный момент времени квадрокоптер находится в точке с координатами (0 0 0) и скоростью в неподвижной СК. На квадрокоптер действует ветер, скорость которого равна , то есть скорость ветра по модулю равна 12,64 м/с. Рассмотрим два случая: с использованием алгоритма стабилизации и без использования.

1) Графики зависимости от времени координат центра масс квадрокоптера и проекций его скорости на оси при отсутствии стабилизации имеют вид:

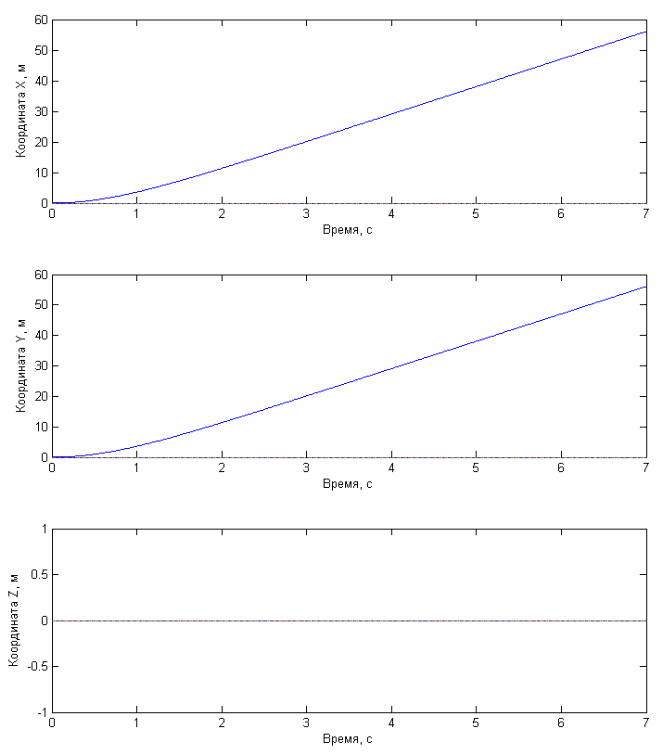
Рис. 4.2.1 Графики зависимости координат центра масс квадрокоптера от времени при отсутствии стабилизации

Рис. 4.2.2 Графики зависимости компонент вектора скорости центра масс квадрокоптера от времени при отсутствии стабилизации

2) Со стабилизацией при тех же начальных данных графики зависимости координат от времени имеют вид:

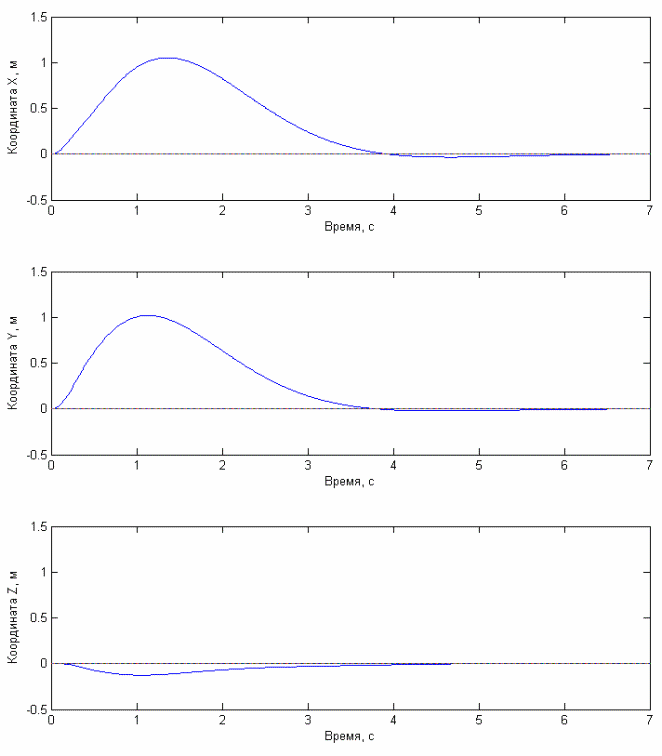
Рис. 4.2.3 Графики зависимости координат центра масс квадрокоптера от времени при использовании алгоритма стабилизации

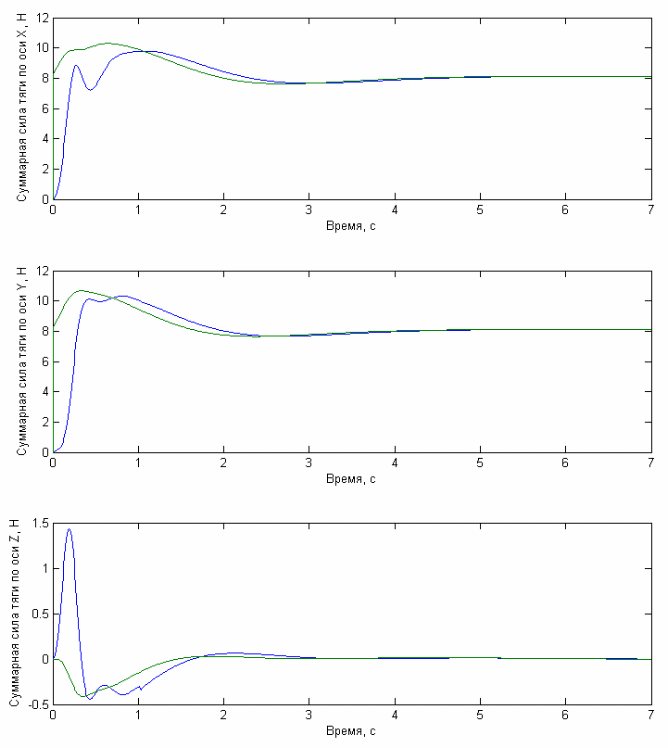
Рис. 4.2.4 Графики зависимости компонент суммарной силы тяги по осям от времени. Синими линиями показана зависимость реальной силы тяги, а зелеными - требуемой.

Пример 2

Имеет смысл рассмотреть более сложный пример.

Пусть начальная скорость квадрокоптера .

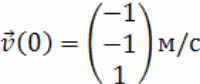Начальный радиус вектор центра масс квадрокоптера

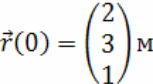
Пусть сила, с которой действует на квадрокоптер ветер равна

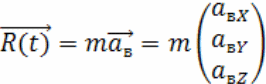
Для моделирования порывистого ветра удобно задать зависимостью ускорения, которое он сообщает квадрокоптеру, от времени.

Таблица 2. Ускорение переданное квадрокоптеру внешней силой

	0 - 5	5 - 10	10 - 15	15 -20	20 - 25	25 - 30
	4	7	6	4	1	0
	8	7	4	4	1	0
	0	0	0	0	0	0

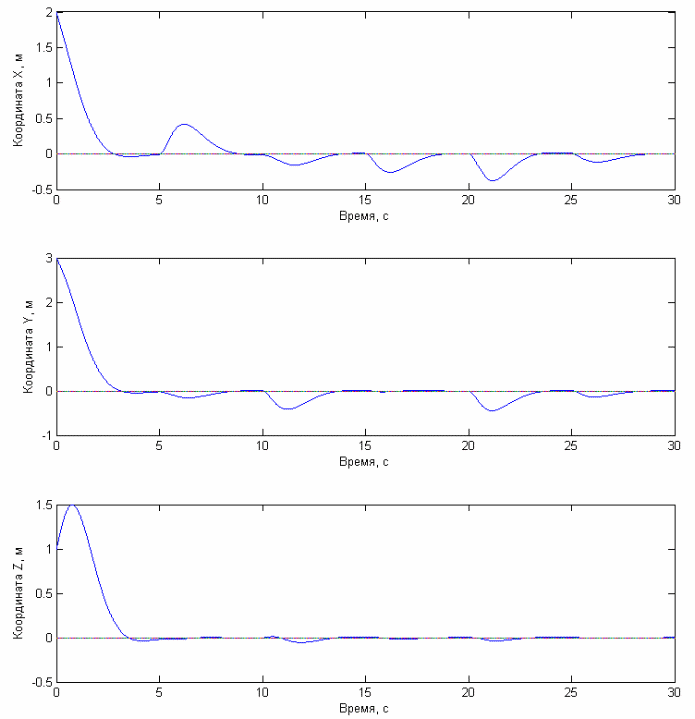
Рис. 4.2.5 Графики зависимости координат центра масс квадрокоптера от времени при использовании алгоритма стабилизации для примера 2.

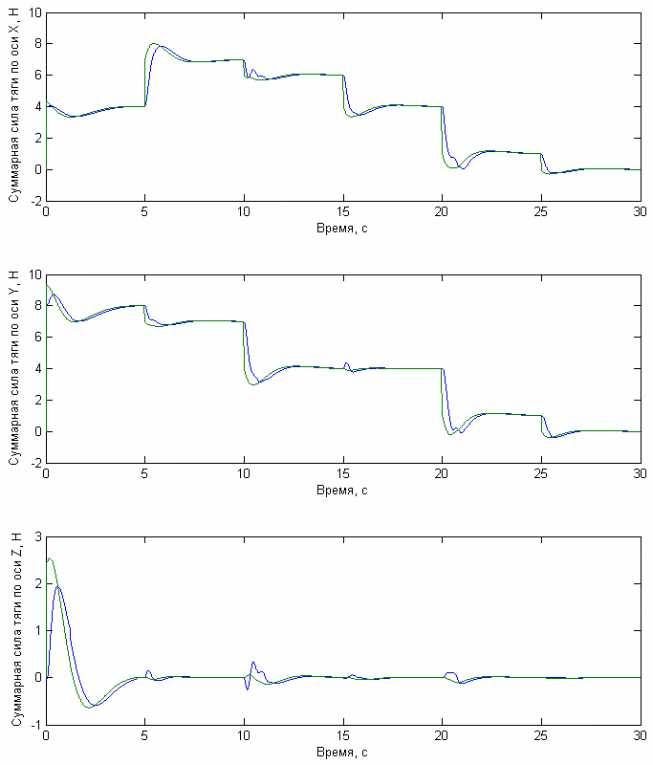
Рис. 4.2.6 Графики зависимости компонент суммарной силы тяги по осям от времени для примера 2. Синими линиями показана зависимость реальной силы тяги, а зелеными требуемой.

Заключение

Целью данной работы является разработка и исследование алгоритма стабилизации квадрокоптера. Для достижения данной цели были решены следующие задачи:

) Разработана математическая модель квадрокоптера

) Разработан алгоритм стабилизации квадрокоптера для этой модели

) Выполнена программная реализация разработанной математической модели в системе MatLab и проведено исследование алгоритма с использованием полученной модели.

В ходе исследования были получены оптимальные коэффициенты необходимые для работ алгоритма и проверена его работа для различных условий. Данный алгоритм требует более детальной проверки с учетом более точной и достоверной модели. В качестве возможных направлений дальнейшего развития математической модели квадрокоптера можно отметить следующие:

) Усовершенствование уравнения движения центра масс квадрокоптера с учетом таких факторов как:. Более точный расчет силы сопротивления воздуха. Более сложная модель ветра

) Усовершенствование уравнения моментов для вращения квадрокоптера с учетом таких факторов как:. Исследование реактивного момента роторов и вывод уравнения вращения квадрокоптера вокруг оси перпендикулярной плоскости квадрокоптера. Расчет влияния гироскопического эффекта вызванного вращением роторов. Сложная геометрическая форма квадрокоптера

) Исследование эффективности предложенного алгоритма стабилизации квадрокоптера по направлению.

квадрокоптер летательный аппарат

Литература

.Беклимишев Д.В. Курс аналитической геометрии и линейной алгебры - Издание 11-е, исправленное - М: Физматлит, 2006.

.Сивухин Д.В. Общий курс физики. Учебное пособие: Для вузов. В 5 т. Т Ι. Механика - Издание 5-е, стереотипное - М: Физматлит, 2002.

.Лазарев Ю. Моделирование процессов и систем в MATLAB. Учебный курс. - Спб.: Питер; Киев: Издательская группа BHV, 2005.

.Денисенко В.В. ПИД-регуляторы: принципы построения и модификации - Современные технологии автоматизации. 2006. № 4. С. 66 - 74; 2007. № 1. С. 78 - 88.