4.Программная реализация модели квадрокоптера и пример работы

.1 Программная реализация модели квадрокоптера

Модель реализована на языке MatLab и состоит из трех подпрограмм:

) Основная программа рассчитывает радиус вектор из точки стабилизации до центра масс квадрокоптера и выводит графики зависимости координат центра масс квадрокоптера в неподвижной СК от времени.

) Блок вычисления текущего значения тяги - подпрограмма, которая на основе рассчитанной требуемой силы тяги вычисляет силы тяги на каждом роторе и вычисляет значения суммарной силы тяги в определенные моменты времени

) Блок расчета силы внешнего воздействия - подпрограмма, вычисляющая значение силы внешнего воздействия в конкретный момент времени. Третья подпрограмма просто представляет собой вектор функцию от времени. На первых двух подпрограммах остановимся подробней.

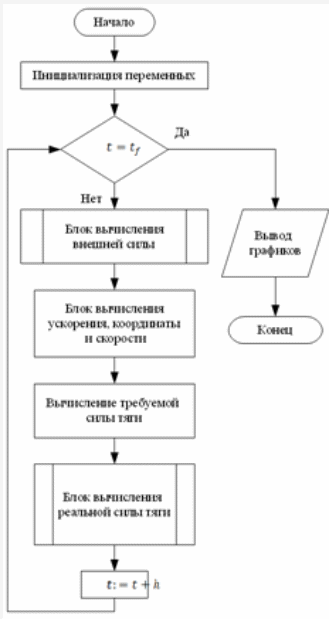
Рис. 4.1.1. Блок схема основной программы

В блоке инициализация переменных задается начальное значение времени и начальные значения скорости , радиус вектора центра масс квадрокоптера и начальные значение суммарной тяги роторов в неподвижной СК, а также значения начальные угловой скорости и углов поворота квадрокоптера в подвижной СК. Внутри цикла в первом блоке вычисляется значения внешней возмущающей силы в моменты времени , и и заносятся в переменные , и . В следующем блоке по формуле (2.3.1) вычисляются значения ускорения в моменты времени , и :

Затем с помощью интегрирования от нуля до текущего значения времени вычисляются текущие значения скорости и радиус-вектора по формулам (2.3.2) и (2.3.3). Интегрирование осуществляется методом Рунге-Кутты. Для этого применяются формулы:

,

Где

В следующем блоке, исходя из полученных значений радиус вектора, скорости и внешней силы по формуле (3.1.1) вычисляется требуемое значение силы тяги . Затем на блок вычисления текущего значения силы тяги подаются переменные , , . На выходе блока получаем значения и в следующий момент времени , и значения суммарной силы тяги , и в моменты времени , и , необходимые для интегрирования методом Рунге-Кутты. Затем увеличиваем t на h и подаем полученные значения на начало цикла. Это повторяется до тех пор, пока не будет достигнуто время . Блок вычисления текущего значения тяги

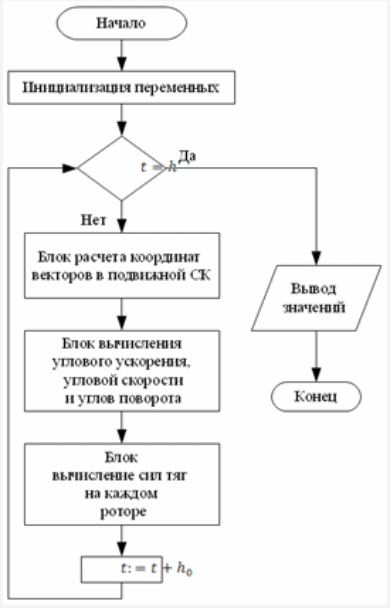
Рис. 4.1.1. Блок схема блока вычисления текущего значения тяги

На вход подаются: , и . Внутренней переменной времени присваивается значение ноль: .

Внутри цикла в первом блоке, исходя из значения , вычисляются матрицы поворота:

,

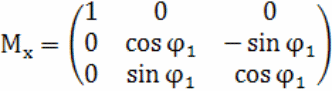
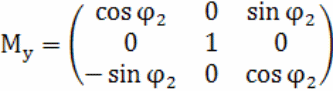
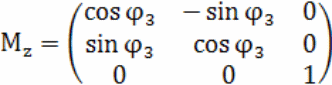
где , и - матрицы поворота вокруг осей OX, OY и OZ соответственно, а -матрица композиции поворотов вокруг трех осей.

Затем пересчитываются координаты векторов , , , и , , , по формулам:

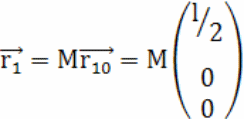
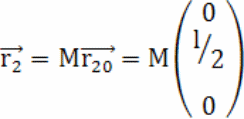
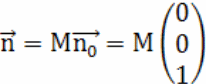
(4.1.16)

(4.1.17)

(4.1.18)

Затем вычисляется значение суммарной силы тяги роторов:

Используя полученные значения во втором вычисляется угловое ускорение по формуле (2.3.5) затем угловую скорость по формуле (2.3.6) и углы поворота вокруг осей подвижной СК по формуле (2.3.7).

В следующем блоке рассчитываются значения тяг на каждом роторе по формулам (3.2.9), (3.2.10), (3.2.11) и (3.2.12). На первом шаге записывается выходное значение , когда записываются выходные значения , когда записывается выходное значение . Затем время увеличивается на шаг и подается на начало цикла. Если цикл завершается и на выходе подпрограмма выдает значения , и и конечные значения и .