3.Алгоритм
.1 Стабилизация квадрокоптера как материальной точки
Пусть
центр масс квадрокоптера находиться в
точке М с радиус вектором
.
Пусть квадрокоптер перемещается со
скоростью
,
на него действуют внешняя сила
.
Требуется стабилизировать квадрокоптер
в точке O. Примем точку O за начало
неподвижной системы координат. Будем
рассматривать квадрокоптер как
материальную точку с массой
.
Для того чтобы стабилизировать
квадрокоптер требуется подействовать
на него с некоторой силой
.
Рис.
Для стабилизации достаточно эффективным является пропорционально дифференциальный алгоритм. Суть его в том, что для того чтобы стабилизировать тело в точке О сила должна состоять из двух составляющих:
составляющей
пропорциональной отклонению от точки
стабилизации с некоторым коэффициентом
составляющей
пропорциональной с некоторым коэффициентом
производной от отклонения,
где коэффициенты и определяются экспериментально.
Кроме того необходимо компенсировать внешнюю силу. Таким образом, требуемая сила должна быть равна:
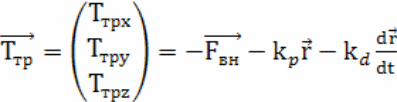
Таким
образом, необходимо чтобы суммарная
сила тяги роторов квадрокоптера равнялась
вектору
.
Так как сила тяги роторов всегда
направлена по нормали к плоскости
квадрокоптера, необходимо повернуть
плоскость квадрокоптера так, чтобы
нормальный к ней вектор
был направлен вдоль
.
То есть решить задачу стабилизации
квадрокоптера по углу.
3.2 Стабилизация квадрокоптера по углу
Положение квадрокоптера относительно связанной системы координат удобно определять с помощью трех углов поворота относительно осей подвижной СК. Требуемые значения углов, на которые необходимо повернуть квадрокоптер относительно каждой из осей нормальной системы координат, вычисляются по следующим формулам:
Где
,
и
- повороты вокруг осей OX, OY и OZ соответственно.
При
этом направление вектора нормали
определяется двумя углами, а именно
поворотом вокруг осей OX и OY. Уравнениями
(2.3.12) определяются текущие значения
этих углов:
и
соответственно. Таким образом, задача
сводится к тому, чтобы стабилизировать
плоскость квадрокоптера углам
и
.
Эту задачу тоже удобно решать
пропорционально-дифференциальным
алгоритмом. Углы поворота определяются
составляющими вектора
по осям OX и OY соответственно. Таким
образом, в качестве управляющего
воздействия для стабилизации по углу
можно рассматривать разность векторов
и
спроецированную на плоскость OYZ, а для
- разность векторов
и
спроецированную на плоскость OXZ. Тогда
для стабилизации по углу
пропорциональной составляющей будет
разность между
и
,
взятая с коэффициентом
,
а дифференциальной - составляющая по
оси OX вектора
,
определенного по формуле (2.3.11), взятая
с коэффициентом
.
Аналогично для стабилизации по углу
.
Величину проекции вектора на плоскость
OYZ можно найти, умножив значение его
длинны на косинус угла между вектором
нормали и плоскостью. Этот значение
этого косинуса равно
.
Аналогично можно найти проекцию на
плоскость OXZ. Таким образом, окончательно
имеем:
Суммарная
сила тяги должна плавно меняться от
некоторого начального значения
до требуемого
,
тогда
,
где
и
начальные значения углов
и
соответственно.
Для
того чтобы наблюдать за объектом нам
необходимо чтобы камеры были направлены
на него. Камеры будут направлены на
объект, если у векторов
и
компоненты по оси OY
и OX
соответственно будут стремиться к нулю.
Этого можно достичь, управляя вращением
в плоскости квадрокоптера. В этом случае
в роли управляющего воздействия будет
разность между суммами тяг роторов
вращающихся по часовой стрелке и роторов
вращающихся против часовой стрелки. В
качестве пропорциональной составляющей
мы возьмем значение сумму значений
и
,
домноженную на коэффициент
,
а в качестве дифференциальной производную
от этой суммы, домноженную на коэффициент
.
Таким образом, получаем:
Уравнения (3.2.4), (3.2.5), (3.2.7) и (3.2.8) составляют систему из четырех уравнений с четырьмя неизвестными, решив ее можно получить выражения для тяг на каждом роторе. Таким образом:
Так
как неизвестен реактивный момент
квадрокоптера данный алгоритм не будет
реализовывать стабилизацию квадрокоптера
по направлению. Поэтому в данном алгоритме
примем
.