§4. Интегрирование по частям

Формула интегрирования по частям

где u, v – дифференцируемые функции.

Применение формулы целесообразно, если интеграл проще исходного интеграла или подобен ему.

В качестве u выбирается функция, которая упрощается в результате дифференцирования, а в качестве – оставшаяся часть подынтегрального выражения, из которой интегрированием можно найти . При этом – одна из первообразных, и, определяя , произвольную постоянную учитывать не будем.

Для некоторых интегралов можно дать общие рекомендации при интегрировании по частям. Эти рекомендации представим в виде таблиц.

Таблица 4

– многочлен от x степени n.

Примеры.

1. Найти .

Решение.

Пользуясь рекомендацией таблицы 4, выберем

, Далее следует найти du и v.

, так как

Заметим, что при нахождении указывается одна из первообразных (произвольная постоянная не нужна). Используя формулу интегрирования по частям, получаем

Итак, мы получили более простой интеграл Найдя его и добавив постоянную C, получаем все семейство первообразных и окончательный ответ:

В дальнейшем для удобства и наглядности будем оформлять запись подстановок определенным образом. Рассмотренный пример выглядит так:

1. Найти

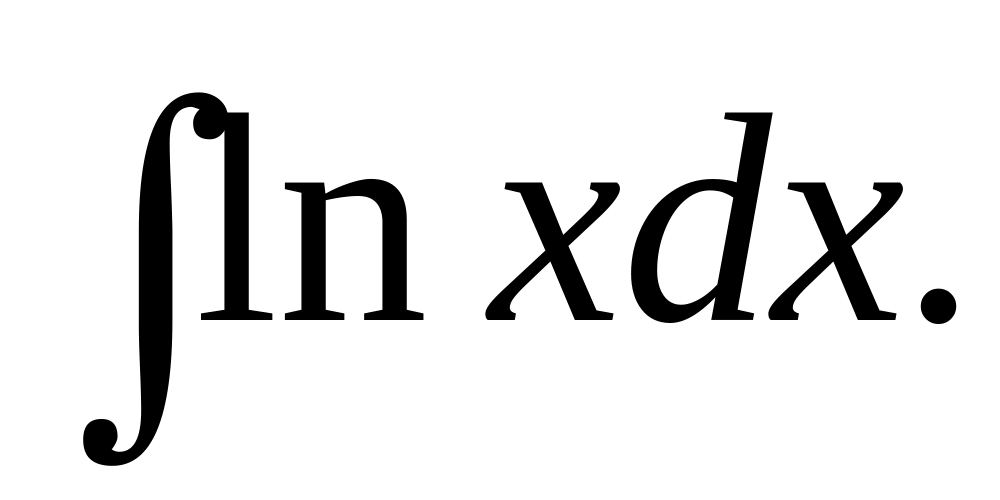
Решение.

Пользуясь таблицей 4, выберем . Получим

3. Найти

Решение.

Обратите внимание на то, что в этом примере интегрирование по частям применено дважды. Причем, на первом этапе было видно, что мы на правильном пути, так как, понизив степень многочлена, мы уже упростили интеграл.

3. Найти

Решение.

Для этого интеграла нет рекомендаций в таблице 4.

, , ,

Мы не получили интеграл проще, а получили подобный. Применим формулу интегрирования по частям еще раз:

,

В правой части мы получили исходный интеграл. Перенесем его в левую часть:

Следовательно,

Осталось добавить произвольную постоянную. Окончательно имеем

Интегралы такого типа называются «возвратными», так как в процессе преобразований мы возвращаемся к исходному интегралу.

4. Найти

Решение.

.

5. Найти

Решение.

Примеры для самостоятельного решения.

Задание	Ответ
1.
2.
3.
4.