30. Модель международной торговли (модель обмена)

Оптимальной моделью обмена является модель, которая позволяет торгующим между собой странам обеспечить взаимную выгоду. Для международной торговли это означает отсутствие значительного дефицита торгового баланса для каждой из стран.

Рассмотрим общий случай, когда торговлю между собой осуществляют n- стран, причем i -я страна выделяет на приобретение товаров, в том числе и внутри страны, сумму x_i, составляющую ее бюджет.

Пусть a_ij— доля госбюджета, которую j -я страна тратит на закупки товаров i-й страны. Тогда после подведения итогов торговли за год i-я страна получит выручку:

p_i=a_i1x₁+a_i2x₂+…+a_inx_n=∑(поjот 1 доn)a_ijx_j, (i=1,n)

или в векторно-матричной форме

р=Ах,где

A - матрица долей госбюджета, идущих на покупку товаров

p - вектор-столбец выручек;

x - вектор-столбец бюджетов стран.

Рассм когда число стран i=3

p₁=a₁₁x₁+a₁₂x₂+a₁₃x₃

p₂=a₂₁x₁+a₂₂x₂+a₂₃x₃

p₃=a₃₁x₁+a₃₂x₂+a₃₃x₃ или в векторно-матричной форме матрица долей гос бюджета 3 гос-в:

Утверждение. Условием бездефицитной торговли является выполнение равенства:

р =х илиАх=х, то есть х_i=р_i (1-16)

Доказательство. Предположим, что для некоторого i -го государства справедливо неравенство x_i>p_i (x_i<p_i).Запишем условие (1.16) с учетом предположения:

p₁=a₁₁x₁+a₁₂x₂+a_1nx_1n=x₁

p₂=a₂₁x₁+a₂₂x₂+a_2nx_1n=x₂

…………………………

p_i=a_i1x₁+a_i2x₂+a_inx_1n>x_i

…………………………

p_n=a_n1x₁+a_n2x₂+a_nnx_1n=x_n

Сложив все равенства и одно неравенство, получим: (∑a_i1)x₁+(∑a_i2)x₂+…+(∑a_in)x_n>∑x_j

Так как суммы в скобке в соответствии с (1.15) равны единице, то получим противоречивое неравенство:

∑x_j>∑x_j

Значит, наше предположение неверно. Аналогично в случае х_i<p_iполучим:

∑x_j<∑x_j

Следовательно, доказательство завершено. Другими словами, условие сбалансированной (бездефицитной) торговли означает, что для каждой страны ее бюджет должен быть равен выручке от торговли.

Уравнение (1.16) означает, что собственный вектор структурной матрицы А, соответствующий собственному числу λ=1, имеет своими компонентами бюджеты стран, осуществляющих бездефицитную международную торговлю. Переписав уравнение (1.16) в виде (A-E)x=0, получим уравнение, позволяющее определить вектор х соответствующий λ=1.

31. модель стабилизации цены на рынке одного товара (модель Эванса)Существует ряд моделей стабилизации цены на рынке одного товара. Среди них можно выделить модели с дискретным и непрерывным временем работы рынка. К модели с дискретным временем относится «паутинообразная модель». В качестве примера модели с непрерывным временем является модель Эванса.Для описания данной модели введем следующие обозначения: d(t)= Ф(p(t)) - спрос на товар во время t; p(t) - стоимость товара во время t; s(t) = Ψ[р(t)]^_ предложение товара в момент t.В качестве допущений, на которых строится модель, принимаются следующие:1)смена цены на товар происходит пропорционально разности между спросом и предложением в данный момент времени, т.е.∆p = γ[d(t)-s(t)]dt, где у — коэффициент пропорциональности (γ> 0);2)спрос на товар падает по линейному закону, т.еd(t)=Ф(p(t)) = а - bp(t),a>0,b>0;3)предложения товара с ростом цены растут по линейному закону,т.е. s(t)= Ψ(p(t)) = α + βp(t),α> 0, β> 0, α<а.Согласно допущениям взаимодействие покупателя и производителя товара происходит таким образом, что цена, которая отображает это взаимодействие, непрерывно приспосабливается до складывающейся ситуации на рынке. Цена растет, если спрос превышает предложения и цена падает, если предложения превышает спрос.Подставив втрое и третье уравнения в первое уравнение, запишем его в виде

∆p/∆t= γ[(a-bp(t)-(α +βp(t))] (2.1)

Перейдя к пределу при ∆t—> 0 получим следующее дифференциальное неоднородное уравнение первого порядка с постоянными коэффициентами:

dp/dt = γ[(a-α)-(b+β)p(t)]

Для его однозначного решения к нему необходимо присоединить начальное условие р(0)=р₀, характеризующее тот факт, что в начальный момент времени t=0 цена =р₀

Если положить dp/dt=0, то из уравнения следует стационарная точка p⁰=(a-α)/(b+β)=const. Так как 0<a>α, b>0, β>0, то p⁰>0.

Из выражения (2.2) следует, что при начальной цене р₀ меньше стационарной p⁰ (p₀<p⁰) dp/dt>0, а, следовательно, происходит рост цены, так как limp(t) —>p^oпри t->беск. При p₀>р⁰происходит падение цены. Другими словами, в первом случае (р₀<р°) цена достигает равновесного значения увеличиваясь, а во втором случае (р_о> р°) уменьшаясь по сравнению с начальной. При этом равновесная цена р°не зависит от начальной цены р₀. Поскольку функции спроса и предложения являются линейными, то их графики представляют собой прямые линии, а тогда равновесная точка есть точка пересечения прямых линий.

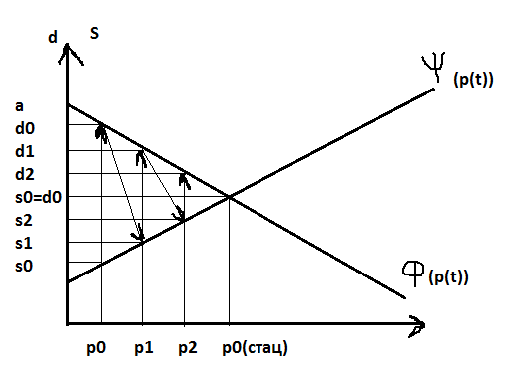
Рис. 2.1 Схема механизма стабилизации цены.