21. Изокванты линейной производственной функции

Изоквантой, или линией уровня на плоскости , называется множество точек плоскости, для которых . Для линейной производственной функции

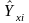=a +b ∙ K + c∙ L

изокванта имеет вид =a - b ∙ K + c∙ L=Y₀=const,

или одна из двух формул ,

).

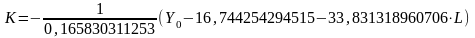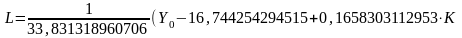Она представляет прямую линию. Для разных значений и , которые формируют точку на конкретнойизокванте, объем производимого продукта равняется значению .

Так как на изокванте справедливо равенство

=a - b ∙ K + c∙ L=Y₀=const,то дифференциал производственной функции равен нулю.

22. Изоклины линейной производственной функции.

Изоклинами называются линии на плоскости наиболее быстрого роста производственной функции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке задается градиентом , то уравнение изоклины можно записать следующим образом: .

В частности для линейной производственной функции имеем: 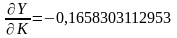, , 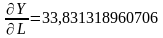а тогда изоклину можно задать уравнением 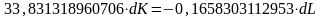, или ,

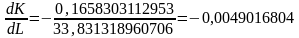которое имеет решение .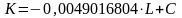

23. Изоквантымультипликатив. Производств.Ф-ции.

Изоквантой, или линией уровня на плоскости KOL, наз-сямн-во точек пл-ти, для кот. F(K,L)=Y₀= const. Для мультипликативной пр-ной ф-цииизокванта имеет вид:

Она предст. степенную гиперболу, асимптотами которой являются оси координат ОКи OL. Для разных значений К и L, кот.формируют точку на конкретной изокванте, объем производимого продукта равняется значению Y₀. Так как на изокванте справедливо равенство , то диф-ал пр-ной ф-ции

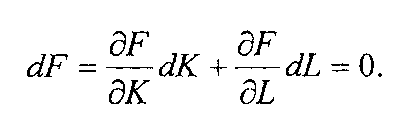
Поскольку в выражении для дифференциала dF/dK>0, dF/dL>0,

то dK и dL должны иметь разные знаки: если dL< 0, что обозначает уменьшение объемов труда, то dK должно быть больше нуля (объем фондов должен увеличиться). Другими словами уменьшение объема одного из ресурсов требует увеличение объема другого ресурса для сохранения объема производимого продукта.

24. Изоклины мультипликативной производственной функции

Изоклинами наз-ся линии на плоскости KOLнаиболее быстрого роста пр-ной ф-ции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке (K, L) задается градиентом

, то уравнение изоклины можно записатьследующим образом:

В частности для степенной мультипликативной производственной функции имеем: dF/dK=α(Y/K), dF/dL=β(Y/L), а тогда изоклину можно задать уравнением (1/α)KdK=(1/β)LdL, которое имеет решениеК =корень((α/β)*L^2+a), где а = К²₀*(α/β)*L²₀ = const.

Здесь К₀ и L₀ - координаты точки, через которую проходит изоклина. Если предположить, а=0, то получим что изоклина представляет собой прямую линиюК = корень(α/β) * L , проходящею через начало координат с коэффициентом наклона прямойкорень(α/β).

25. Коэф.Эластич.Производ.Ф-ии 2х переменных.

Важнымихар-ми производ. ф-ииявл. коэффициентыэластич. выпуска по ресурсам.

Е_К = - 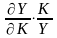Е_L= - 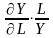Т.е. они равняются отношению предельной производительности соответ. рес-са к его сред.производ-ти.

Коэф. эластич. показывают, на сколько % изменится выпуск прод-ции при увеличении затрат одного рес-са на 1 % и сохранении значенияядр.рес-са.

На ряду с понятием эластич.выпуска по затратам рес-сов в эк.анализе применяется понятие эластич. взаимозаменяемости рес-сов. При дв-нии вдоль изокванты F(K,L)=Y₀=const вместе с координатами точки (K,L) изменяется зн-е γ_LK , и велечина отношения затрат L/K. Считая,что они связаны функционально: L/K=ϕ(γ_LK), в предположении,что ф-я дифференцуруемая,вычислим эластичность этой функции:

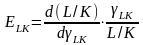. Коэф. эластич. взаимозаменяемости рес-сов Е_LKпоказыв. на сколько % должно измениться отношение затрат рес-сов,чтобы предельная норма заменяемостирес-сов увелич. на 1%.

Е_LK принимает самые различные зн-я на промежутке [0;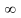 ). Чем выше зн-е коэф. эластич.взаимозамен.рес-сов,тем в более широких пределах рес-сы могут заменять друг друга. При Е_LK=0 возможность замены рес-сов отсутствует.При Е_LK→ рес-сы могут заменять друг другав самых широких пределах.

26.Опред-е масштаба и эфф-тистр-ва с помощью производ.ф-ции.Анализируя рес-сы,обеспечив.рост эк-ки выделяют: 1)- интенсивный (обеспечив.ростпрод-та за счет увелич.эфф-ти использования рес-сов); 2)- экстенсивный (за счет увелич. объемов затрат рес-сов).С помощью производ.ф-ии можно выяснить масштабы использ.рес-сов. Только если выражено в соизмеримых ед.: -стоимостных;- относительных.Рассмотрим мультипликат-ю производ.ф-ию,кот. будет в безразмероной форме.

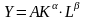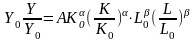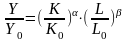- размерная форма. или , тк. 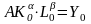. Здесь Y₀,K₀,L₀ – зн-я объема выпуска продукции,затрат фондов и труда в базовом году. Если использовать выпуск.продукцию и рес-сы в безразмерн.форме и обозначить их соответств. через 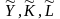, то мультипликат.производ.ф-я может быть записана в ви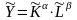де: , где .

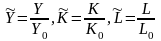Под эфф-тью пр-вапоним. отношение результат пр-ва к затратам рес-са.В рассмотр. модели Кобба-Дугл.учитыв. два вида затрат: 1)затраты прошедшего труда (фонды, капитал) 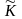;2) затраты живого труда 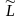.Соответ.будет два частных показателя эфф-ти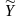 / - фондоотдача; / - продуктивность.

Т.к. приведенные частные показатели эфф-ти безразмерны,то можно ввести средн.зн-е эфф-ти:

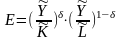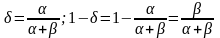( сред.геом.взвешенный частный показатель). - относит эластичности, играющие роль весовых коэф.

Из выражения для показателя эффективности следует, что с помощью коэффициента экономической эффективности производственную функцию можно представить в форме, которая по внешнему виду совпадает с функцией Кобба – ДугласаY = EK^aL'-^a.

Отличие заключается в том, что в представленной форме показатель эффективностиЕ не является постоянным коэффициентом, а является функцией от ресурсов К и L.

Поскольку масштаб производства, который обозначим через M, выражается в объемах израсходованных ресурсов, то, проводя аналогичные рассуждения, как и построении общего показателя экономической эффективности, примем среднегеометрическое взвешенное использование ресурсов как масштаб производства M= (без Ycчертой, вместо α – σ, вместо β – 1-σ). Тогда =E*M