17. Метод наименьших квадратов для линейнойф-и регрессии

Общий вид линейной функции регрессии: у_х=а+bx. Характеризуетет семейства прямых, каждое из которых характеризуется конкретными значениями коэффициентов а и Ь.Наилучшей из всего множества прямых для рассматриваемой выборки является та прямая, которая на плоскости хОу расположена "ближе" всего, в определенном смысле, к опытным точкам. В качестве меры близости прямой и некоторой точки на плоскости можно выбрать расстояние между ними. При этом под расстоянием следует понимать модуль разности между опытным (наблюдаемым) значением результирующей величины и теоретическим.

В качестве критерия близости между прямой и множеством точек на плоскости целесообразно выбрать минимум суммы квадратов этих расстояний. Е=∑(yi-a-∑bx_i)^2->min. Здесь считается, что y_t и x_i - известные статистические данные; аи b — неизвестные параметры (коэффициенты) функции регрессии. Поскольку функцияЕ непрерывна, выпукла и ограничена снизу нулем, то она имеет минимум. Изложенная идея минимизации суммы квадратов отклонений (на плоскости расстояний) опытных от теоретических значений объясняемой переменной положена в основу метода наименьших квадратов.

Для нахождения коэфa иbлинрегр, минимизирующих ф-ю, необходимопродифференцировать ее по а и b и приравнять производные нулю:

После преобразований окончательно будем иметь

; ; ;

; ; ;

; ; .

После применения метода наименьших квадратов можно получить систему уравнений в векторно-матричной форме:

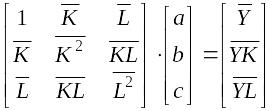
В рез-те решения будем иметь (далее метод Крамера)

МНК для степенной ф-и регрессии

Ф-я регрессии в данном случае рассматривается как эк-мат модель.у_хi(с шапочкой)=ах^b. Относится к нелинейным, однако, ее можно линеаризовать,т.е. привести к линейной. Линеаризация осуществляется с помощью логарифмирования.

Степенная ф-я после логарифмирования будет иметь вид lgy=lg(ax^b)=lga+lgx^b=lga+blgx. Обозначимlgy=Y, lgx=X, A=lga =>Y=A+bX.

Далее применяем метод наименьших квадратов и метод Крамера как и для линейной модели.

18. Решение систем методом Крамера

; ; ;

; ; ;

; ; .

После применения метода наименьших квадратов можно получить систему уравнений в векторно-матричной форме:

Решение системы, т.е. нахождение параметров модели, можно выполнить методом Крамера. Для его реализации необходимо вычислить четыре следующих определителя:

,

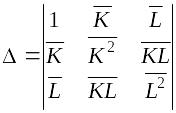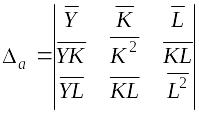
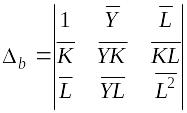
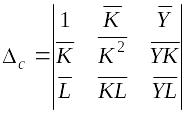
Тогда вычисление параметров модели можно осуществить по следующим формулам:

, , .

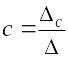19.(20) Неоклассическая мультипликативная производств.Ф-ция.

Производственная функция отображает зависимость результата (объема) производства от затрат ресурсов.

Производственная функция наз-сянеоклассической мультипликативной ф-цией, если она непрерывна и удовлетворяетусл-ям:

1) F(0,L) = F(K,0) =0 - отсутствие одного из ресурсов не обеспечивает результата (продукта) производства;

2) - с ростом объемов ресурсов растет и объемвыпускаемого продукта;

3) - с ростом объемов ресурсов скорость ростаобъема продукта снижается;

4) - с неограниченным ростом объема одного из ресурсов выпуск продукта неограниченно растет.

Мультипликативная пр-ная ф-цияявл. степ.ф-цей и задается следующим аналит. выр-ем:

гдеА- коэффициент технического прогресса; α, β- показатели степени производственной ф-ции соответственно при ср-вах пр-ва и рабочей силе.

Как отмечалось, в частном случае, когда мультипликатив. пр-ная ф-ция называется функцией Кобба - Дугласа.

Для интерпретации показателей степени α и β воспользуемся выражением для коэффициента эластичности через натуральный логарифм. Эластичность может рассматриваться как логарифмическая производная. Тогда будем иметь, что эластичность продукта по фондам Е_k, и эластичность продукта по труду Е_L, можно вычислить по следующим соотношениям:

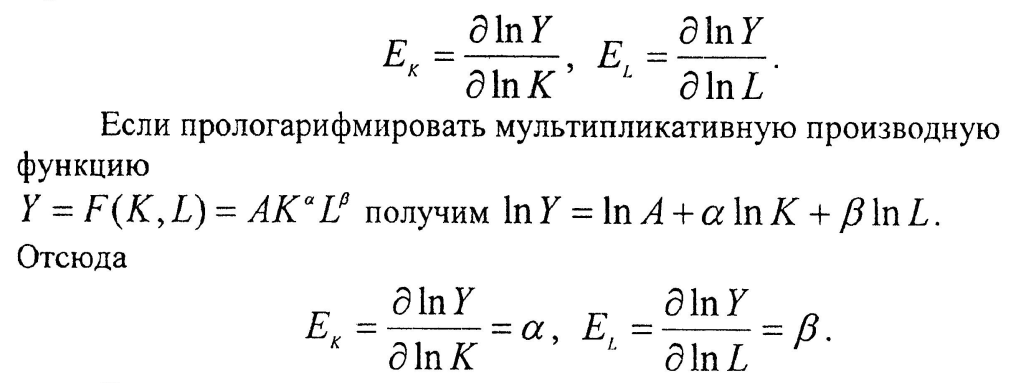
В качестве примера мультипликативной производственной функции можно привести функцию валового выпуска продукции Российской Федерации, построенную по выходным статистическим данным за 1960 - 1994 годы. Она имеет вид Y = F(K, L) = 0,931К^0,539L^0,594