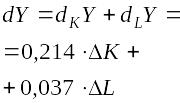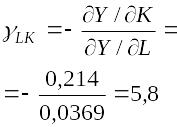15.(16) Типы производственных функций 2х переменных.

Степенная производственная функция.Среди производственных функций, используемых для описания производства в масштабах страны, важное место занимают степенные производственные функции. Для двух ресурсов они имеют вид

Дост-ва такой ф-ции состоят, во-первых, в наличии небольшого числа параметров, имеющих явный эк. смысл, и, во-вторых, в существовании производных высших порядков. Кроме того, степенные производственные ф-ции с помощью логарифмирования сводятся к функциям линейным (относительно новых логарифмических переменных), что удобно для оценки параметров по статистическим данным.

впервые были использованы американскими учеными К. Коббом и П. Дугласом для изучения связей между национальным доходом и двумя важнейшими факторами производства - рабочей силой и основными производственными фондами. Однако сегодня принято, что для классической производственной функции типа Кобба - Дугласа существует связь между показателями степеней, а именно α+β= 1.

Функция с фиксированными пропорциями ресурсов (функция Леонтьева)

Эта функция имеет вид: Y=F(K,L)=Amin(K/a;L/b), где a, b – параметры. параметры характеризуют удельные затраты капитала и труда, необходимые для выпуска продукции в количестве A. Функция Леонтьева предназначена в основном для моделирования строго детерминированных технологий, которые не допускают отклонения от технологических норм и нормативов использования ресурсов на единицу продукции. Как правило, они используются для формализованного описания полностью автоматизированных объектов.

Линейная функция.

характерно, что предельные эффективности (производительности) по каждому из ресурсов являются величинами постоянными, равными по величине коэффициентупри соответствующем аргументе (ресурсу): дY/дK=a, дY/дL=b.

Линейная функция применяется при моделировании крупномасштабных систем (крупная компания, отрасль, страна), у которой производство продукции есть результат одновременного функционирования большого числа различных технологий.

Производственная функция Алена.

Функция Алена при положительных коэффициентах b, сиспользуется для формализованного описания производственных процессов, у которых чрезмерный рост одного из ресурсов негативно влияет на объем выпуска продукции. Такая функция применяется для описания мелкомасштабных производственных систем с ограниченными возможностями переработки ресурсов.

Производственная функция CES.Ф-цияCESисп-ся в случае отсутствия точной информации относительно уровня взаимозамещаемости производственных ресурсов, однако имеется основание считать, что уровень производства принципиально не изменится при изменении объемов использования ресурсов. Это характерно для случая, когда экономическая технология имеет свойство определенной устойчивости относительно определенных пропорций ресурсов. Функция используется для моделирования широкого диапазона производственных процессов и имеет вид

14. Производственная ф-я 2х перем.

Производственная ф-ция одной перемен. - ф-ция, независимая перем. кот. прин. зн-я объемов затраченного р-са (ф-ра пр-ва), а завис. переем. представляет собой зн-я объемов выпускаемой прод-ции. Ее представляют в традиц. форме записи математической функции y= f(x). При этом для нее характерно, что как у так и х принимают только положит.зн-я.

На практике чаще используются производственные функции нескольких переменных. Так, например, Y = F(K, L) - производственная функция, которая описывает зависимость объема выпускаемой продукции Yот затрат двух видов ресурсов: рабочей силы L (трудовые ресурсы) и средств производстваК (основные производственные ресурсы).

Выясним, как можно охарактеризовать изменение потребления каждого из ресурсов на выпуск продукции. Очевидно, выпуск будет зависеть только от одного из ресурсов, если количество другого остается неизменным. Оставляя без изменения величину трудовых ресурсов L, увеличим основные производственные фонды К на ∆К . Произошедшее при этом изменение выражается разностью

∆_kY = F(K + ∆K,L)-F(K,L).

Поделив ∆_KY на∆К получим то дополнительное количество продукции (в стоимостном или натуральном выражении), которое, в среднем, может быть получено в результате увеличения основных производственных фондов на единицу (на один рубль или на одну штуку). Отношение ∆_KY/∆К в экономическом анализе называют средней эффективностью (производительностью) средств производства или средним продуктом по средствам производства.

Если в качестве ресурса выступают основные производственные фонды, то средний продукт представляет собой фондоотдачу. Трудовым ресурсам соответствует такой средний продукт как трудоотдача или производительность труда.

Очевидно, выпуск продукции, приходящийся на различные дополнительные единицы ресурса, также различен. Характеристика ресурсоотдачи будет тем точнее, чем меньше будет величина ∆К (или ∆L).

Вычислив ΔУ/ ΔК=lim∆_KY/ ∆К, найдем прирост выпуска продукции,соответствующий увеличению затрат средств производства на «малую единицу». Указанный предел используют в экономическом анализе эффективности производства и называют предельной эффективностью (производительностью) ресурсов или коэффициентом приростной ресурсоотдачи.

Вторая производная d²Y /dК² (или d²Y /dL²) определяет характер измененияпредельной эффективности соответствующего ресурса. Если она больше нуля, то с увеличениемК (или L) возрастает эффективность соответствующего ресурса.

В таблице 1.2 приведены основные характеристики производственной функции, зависящей от двух факторов (ресурсов).

№п/п	Вычислительная формула	Название	Экономический смысл
1	Y=F(K,L)	Производственная функция	Выражает зависимость объема выпуска от ресурсов
2	Y=F(K,L)=Y0	Изокванта (линия постоянного выпуска)	Линия в пространстве ресурсов, координаты которой представляют комбинации затрат ресурсов, обеспечивающие в объеме Y0 выпуск продукции
3	,	Частная производная (Предельная эффективность объема выпуска по ресурсу K (или L))	Прирост выпуска продукции, соответствующей увеличению затрат ресурса K на «малую единицу»
4	,	Частная вторая производная (Темп изменения объема выпуска по ресурсу K (или L))	Определяет характер изменения предельной эффективности соответствующего ресурса
5		Частный дифференциал	Приближенное значение объема продукции, произведенной за счет (или )
6		Полный дифференциал	Приближенно выражает изменение выпуска продукции при небольших изменениях затрат обеих ресурсов
7		Предельная норма замещения (коэффициент эквивалентнойзаменяемости ресурсов)	Показывает, какое к-во одного ресурса может быть высвобождено при увеличении затрат другого ресурса при сохранении объема выпуска