12. Эластичность функции спроса

Рассмотрим график функции спроса х = х(р), где х(р) — спрос, а р — цена. Из графика (рис. 2.4) следует, что чем выше цена р, тем меньше спрос х = х(р) . Согласно геометрическому смыслу производной

x’(p₀)=tgβ, где β=(π/2)+α

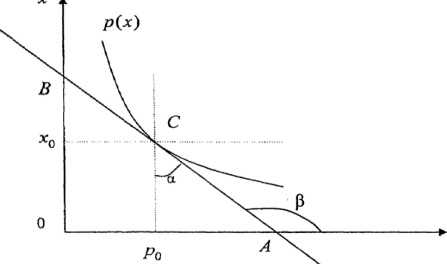
Рис. 2.4

Аналогично, как для функции предложения, можно показать, что эластичность функции спроса находится в пределах -беск< E_x< 0, поскольку перед отношением длин стоит знак минус.

Очевидно, как и для эластичности предложения, знак эластичности спроса будет определяться знаком производной, поскольку графики функций располагаются в первой четверти, то есть значение функции и аргумента величины положительные (х > О, р>0).

Различают следующие виды эластичности спроса по цене: эластичность единичная, эластичный спрос, неэластичный спрос, совершенно эластичный спрос, совершенно неэластичный спрос.

Под единичной эластичностью понимают случай, когда Е_x= - 1, то есть когда на каждый процент изменения цены спрос количественно изменяется на один процент. При эластичном спросе (E_x< — 1) величина спроса изменяется в большей мере, чем цена, и, наоборот, при неэластичном спросе ( — 1 < E_x< 0). Совершенно эластичный спрос определяет ситуацию, при которой величина спроса бесконечно.изменяется при малом изменении цены (E_x=-беск). Совершенно неэластичный спрос (E_x= 0) обусловливается ситуацией, когда величина спроса не изменяется при любом изменении цены.

11. Свойства эл-ти.1. Пусть даны непрерывные функции Кроме того Тогда для функции ее эластичность Е_y будет удовлетворять следующему условию: Доказательство

2. Пусть функции Тогда эластичность произведения функций y(x)* z(x) равна сумме их эластичностей, а эластичность частного- разности их эластичностей, т.е.

Доказательство

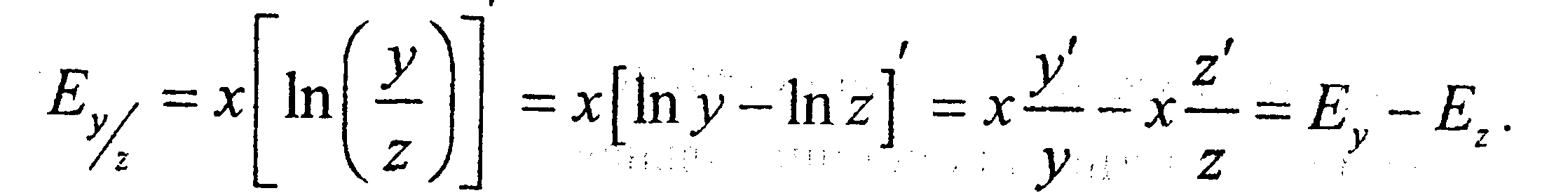
3. Пусть дана сложная функция y= y(x), где x= x(t), Тогда эластичность функции y(t) удовлетворяет равенству

Доказательство

4. Пусть для функции y=f(x) существует обратная функция x= g(y).тогда эластичность обратной функции удовлетворяет соотношению:

ДоказательствоПоскольку для обратной функции выполняется тождество f(g(y))=y, то применяя cв-во 3 получим

Примечание: эластичность является величиной безразмерной

13. Эластичность функции предложения

Рассмотрим график функции (рис. 2.3) предложения Р = p(x) и эластичность Е_pв точке х = х₀:

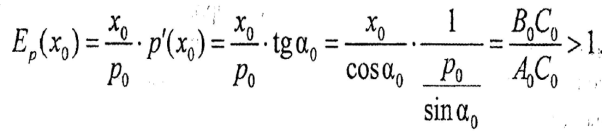
Таким образом, с учетом геометрического смысла производной р’(х) = tgα₀ геометрический смысл эластичности — это отношение длины касательной от точки касания до точки пересечения касательной с осью ординат к длине касательной от точки касания до точки пересечения с осью абсцисс. Из приведенных примеров геометрического смысла эластичности функции предложения следует, что 0<Е_p<+беск.

С экономической точки зрения предложение считается эластичным (Е_p>1), если изменение рыночной цены товара на определенную величину в процентах влечет за собой более значительное в процентах изменение объема производства и предложения данного товара. Е_p = 1 соответствует случаю, когда изменение рыночной цены товара на определенную величину в процентах влечет за собой такое же в процентах изменение объема производства и предложения товара. Неэластичным считается предложение, если изменение рыночной цены на 1% вызывает изменение объема производства менее чем на 1% ( 0<Е_p<1).