8.(9) Построение ф-ий спроса и предложения методом наименьших квадратов.

В качестве исходных данных для построения ф-ии спроса и предложения выступают данные nнезав наблюдений за спросом (предлож) и соответствующей ему цене.

Эти набл можно представить в виде вектор столбца Х и У. эл-ты столбца х выступ в кач-везнач цены, фиксируемой в iом опыте. Вектор столбец у сост из компонент представл собой знач спроса (предлож), фиксируемых в каждом iом опыте.

Ф-испр и предл могут быть как лин, так и нелин. В случлин ф-и она им вид: у_х=а+bx. Хар-ет семейства прямых, каждое из которых характеризуется конкретными значениями коэффициентов а и Ь, Наилучшей из всего множества прямых для рассматриваемой выборки является та прямая, которая на плоскости хОу расположена "ближе" всего, в определенном смысле, к опытным точкам. В качестве меры близости прямой и некоторой точки на плоскости можно выбрать расстояние между ними. При этом под расстоянием следует понимать модуль разности между опытным (наблюдаемым) значением результирующей величины и теоретическим.

В качестве критерия близости между прямой и множеством точек на плоскости целесообразно выбрать минимум суммы квадратов этих расстояний. Е=∑(yi-a-bx_i)^2->min. Здесь считается, что y_i и x_i - известные статистические данные; а и Ъ — неизвестные параметры (коэффициенты) функции регрессии. Поскольку функцияЕ непрерывна, выпукла и ограничена снизу нулем, то она имеет минимум. Изложенная идея минимизации суммы квадратов отклонений (на плоскости расстояний) опытных от теоретических значений объясняемой переменной положена в основу метода наименьших квадратов.

Если необходимо оценить коэфф-ты линейной ф-ии спроса, то применяют непосредственно метод наименьших квадратов p(x)=Co+C1(x). Если нелинейная ф-ия – используют линеаризацию. Самостоятельно применяют метод наим. кВ. для нелинейной ф-ии спроса, т.е. линеаризируют функцию зависящую .

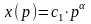10. Определение эластичности функции.

Эластичностью E_xy(x₀) непрерывной функции y=f(x) в точке x= x₀ называется предел отношения относительного приращения ф-ии в точке x₀ к относительному приращению аргумента в точке x₀, когда абсолютное приращение ∆х→0.

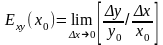
Из определения следует, что при малых ∆х: 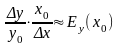, т.е. Эластичность – коэф. пропорциональности между относительными изменениями величины ф-ии и аргумента. Показываетна сколько % измениться относительное приращение ф-ии, еслт изменить на 1 % относительное приращение аргумента. Из анализа определения следует выражение для эластичности через производную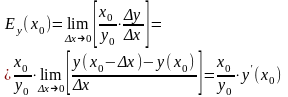

Следовательно, если ф-я y(x) на промежутке (a,b) дифференцируема, то для нее можно вычислить производную в точке х℮(a,b) эластичность E_y(x)=(x/y)*y^/(x)

Формулы расчета коэф эл для широко исп типов ф-й.

Линейная y=a+bx	y’x=b	Ey(x)=bx/(a+bx)
Квардратичнтрехчy=a+bx+cx2	y’x=b+2cx	Ey(x)=(b+2cx)x/(a+bx+c2)
Обратно пропорцy=a/x	y’x=-a/x2	Ey(x)=-1
Показат y=abx	y’x=abxlnb	Ey(x)=xlnb
Степенная y=axα	y’x=aαxα-1	Ey(x)=α
Полулогарифмическая y=a+blnx	y’x=b/x	Ey(x)=b/(a+blnx)
Логистическая y=a/(1+b*e-αx)	y’x=a*bαe-αx/(1+b*e-αx)^2	Ey(x)=bαx/(eαx+b)
Обратная y=1/(a+bx)	y’x=-b/(a+bx)^2	Ey(x)=-bx/(a+bx)

Следуют особо обратить внимание на степ ф-ю. для нее коэф эл представл собой пост в-ну равную пок-лю степени альфа.

Как частный случ степенной ф-и, обрпропрорц ф-я (α=-1) имеет E_y(x)=-1