
- •Абсолютные и относительные величины в экономическом анализе.
- •8.(9) Построение ф-ий спроса и предложения методом наименьших квадратов.
- •10. Определение эластичности функции.
- •12. Эластичность функции спроса
- •13. Эластичность функции предложения
- •15.(16) Типы производственных функций 2х переменных.
- •14. Производственная ф-я 2х перем.
- •17. Метод наименьших квадратов для линейнойф-и регрессии
- •18. Решение систем методом Крамера
- •19.(20) Неоклассическая мультипликативная производств.Ф-ция.
- •21. Изокванты линейной производственной функции
- •22. Изоклины линейной производственной функции.
- •23. Изоквантымультипликатив. Производств.Ф-ции.
- •24. Изоклины мультипликативной производственной функции
- •25. Коэф.Эластич.Производ.Ф-ии 2х переменных.
- •27. Построение балансовой модели
- •28. Продуктивные модели Леонтьева.
- •30. Модель международной торговли (модель обмена)
Абсолютные и относительные величины в экономическом анализе.
Абсолютные – характеризуют объемные или денежные размеры экономических показателей. Дают представление о запасах сырья, материала, размерах перевозимого груза, объемах денежных средств. Бывают: 1) Натуральные – экономические показатели в натурально вещественной форме, выражаются в длине, массе, объеме, мощности, числе построенных домов. 2) Трудовые ед. – чел/час, чел/день, чел/год. 3) Стоимостные – руб, доллар, евро – характеризуют ВВП, доход, расход, величины ОС, издержки производства и т.д.
Относительные – отношение абсолютных или других относительных величин и выражают кол-во единиц одного показателя на единицу другого. Величина с кот.производится сопоставление (знаменатель) называетсяся базисной. Выражаются в безразмерных коэффициентах, % или в единицах присущих соотносимым абсолютным величинам. Различают: 1) Интенсивности – в результате сопоставления разноименных, связанных между собой абс. величин на момент (за период) или характеризуют степень развития экономического явления. 2)Динамики – характеризуют изменение во времени плановых заданий и относительных величин интенсивности. 3) Выполнения плана – для контроля над ходом выполнения планов. Вычисляются как отношение фактического уровня абс. или отн. величин к плановым их значениям. 4) Сравнения – характеризуют сравнительные размеры одноименных величин в одинаковый период времени, но к разным объектам. 5) Структуры – характеризуют доли отдельных частей в целом.
2.
Суммарные, средние и предельные величины
в экономическом анализе.1)
Суммарные величины
в экономике – абсолютные величины;или
(в общем случае) величина, для кот.существует
средняя или предельная величина. Она
рассматривается как функция F(x),
у функции может быть аналитическое или
табличное задание. Соответственно может
иметь непрерывный, либо дискретный
характер изменения. Также суммарнаявеличина
в экономике железнодорожного транспорта
– доход или издержки как функции объема
перевозимого груза; объем перевозимого
груза как функция ресурсов, в качестве
которых выступает труд и капитал и др.2)
Средняя величина
– определяется как отношение суммарной
величины к независимой переменной Пример
– средняя фондоотдача, средний доход,
средний грузооборот. 3)
Предельная (маржинальная) величина
–
определяется как производная суммарной
величины F(x)
по независимой переменной х: MF(x)=F'(x)
– в случае, когда независимая переменная
х непрерывна. Если суммарная величина
меняется дискретно, то MF(x)
– это отношение изменения ∆F(x)
суммарной величины F(x)
к вызвавшему это изменение приращению
∆х независимой переменной х: MF(x)=
∆F(x)/
∆х. в это случае предельную величину
можно интерпретировать как изменение
суммарной величины, вызванное увеличение
независимой переменной на масштабную
единицу. Предельная величина, как и
суммарная и средняя, может задаваться
в виде аналитической формулы или таблично
и представляться графически.В экономике
часто приходится решать задачи на
нахождение одной величины по
другим(например, среднего или предельного
дохода по суммарному). В этом случае
используется аппарат дифференциального
и интегрального исчисления функции
одной переменной.
Пример
– средняя фондоотдача, средний доход,
средний грузооборот. 3)
Предельная (маржинальная) величина
–
определяется как производная суммарной
величины F(x)
по независимой переменной х: MF(x)=F'(x)
– в случае, когда независимая переменная
х непрерывна. Если суммарная величина
меняется дискретно, то MF(x)
– это отношение изменения ∆F(x)
суммарной величины F(x)
к вызвавшему это изменение приращению
∆х независимой переменной х: MF(x)=
∆F(x)/
∆х. в это случае предельную величину
можно интерпретировать как изменение
суммарной величины, вызванное увеличение
независимой переменной на масштабную
единицу. Предельная величина, как и
суммарная и средняя, может задаваться
в виде аналитической формулы или таблично
и представляться графически.В экономике
часто приходится решать задачи на
нахождение одной величины по
другим(например, среднего или предельного
дохода по суммарному). В этом случае
используется аппарат дифференциального
и интегрального исчисления функции
одной переменной.
3. Общая характеристика математических функций, используемых в экономике. Функция – это правило, по которому одной величине х из множества Х соответствует другая величина у из множества Y. х – переменная или аргумент, величина от которой ф-я зависит, y – ф-я или зависимая переменная. В экономике: х – фактор, объясняющая вел-на, у – результирующая или объясняемая вел-на. В эк-ке большое число ф-ий: -производственная (результирующая вел-на – это объем пр-ва, а фактор – это ресурсы, капитал, труд), -издержек пр-ва, -дохода, -полезности, -спроса, -предложения, -непрерывных % и т.д. Ф-ции в эк-ке могут быть заданы с помощью аналитических зависимостей, графически, таблично.
Классификация математических ф-ций для описания связи 2-х переменных достаточно широкая. Ф-ии для описания связи 2-х элементов: 1) линейная y=a+bx, 2) квадратичная y=ax²+bx+c, 3)кубическая y=ax³+bx²+cx+d, 4) обратнопропорц. y=a-b/x (x≠0), 4)показательная y=abx. 5) степенная y= a · xb.
более сложные ф-ции
y=1/(a+bx) y=a+bx+c/x y=a+blgx y=1/(a+bx+cx2)y=a/(1+be-cx) lgy=a+bx+cx2
Пример: 1) Ф-я потребления энергии y от объема производимой продукции (x) – это линейная ф-я y=a+bx. Если разделить на x, то получим y/x=a/x+b=z – это выражение зависимости удельного расхода электроэнергии на ед. прод-ииz в зависимости от объема выпущенной прод-ииx в виде уравнения равносторонней гиперболы. 2) В эк-ке часто применяется многочлен 2ой степени y=ax²+bx+c. При определении x (аргумента) – график может быть симметричен, эти ф-ии описывают – з/п работников физического труда под возрастом, зависимость урожайности от кол-ва внесенных удобрений. Кривая Филипса – хар-ет нелинейную зависимость междуу нормой безработных и % прироста з/пy=a+b/x. Кривая Эйнгеля – сформулировал закономерность согласно которой с ростом дохода, доля его расходуемого на продовольствие уменьшается y=a-b/x, у – доля на продовольствие.
4. Типы функций одной и нескольких переменных, используемых в эк. мат. моделях.Функция – это правило, по которому одной величине х из множества Х соответствует другая величина у из множества Y. х – переменная или аргумент, величина от которой ф-я зависит, y – ф-я или зависимая переменная. В экономике: х – фактор, объясняющая вел-на, у – результирующая или объясняемая вел-на. В эк-ке большое число ф-ий: -производственная (результирующая вел-на – это объем пр-ва, а фактор – это ресурсы, капитал, труд), -издержек пр-ва, -дохода, -полезности, -спроса, -предложения, -непрерывных % и т.д. Ф-ции в эк-ке могут быть заданы с помощью аналитических зависимостей, графически, таблично. Классификация математических ф-ций для описания связи 2-х переменных достаточно широкая. Ф-ии для описания связи 2-х элементов: 1) линейная y=a+bx, 2) квадратичная y=ax²+bx+c, 3)кубическая y=ax³+bx²+cx+d, 4) обратнопропорц. y=a-b/x (x≠0), 4)показательная y=abx. 5) степенная y= a · xb. болеесложныеф-ции
y=1/(a+bx) y=a+bx+c/x y=a+blgx y=1/(a+bx+cx2) y=a/(1+be-cx) lgy=a+bx+cx2
Типы
производственных функций 2х
переменных.Степенная
производственная функция.Среди
производственных функций, используемых
для описания производства в масштабах
страны, важное место занимают
степенныепроизводственные функции.
Для двух ресурсов они имеют вид![]() Дост-ва
такой ф-ции состоят, во-первых, в наличии
небольшого числа параметров, имеющих
явный эк. смысл, и, во-вторых, в существовании
производных высших порядков. Кроме
того, степенные производственные ф-ции
с помощью логарифмирования сводятся к
функциям линейным (относительно новых
логарифмических переменных), что удобно
для оценки параметров по статистическим
данным. впервые
были использованы американскими учеными
К. Коббом и П. Дугласом для изучения
связей между национальным доходом и
двумя важнейшими факторами производства
- рабочей силой и основными производственными
фондами. Однако сегодня принято, что
для классической производственной
функции типа Кобба - Дугласа существует
связь между показателями степеней, а
именно α+β=
1.Функция
с фиксированными пропорциями ресурсов
(функция Леонтьева)Эта
функция имеет вид: Y=F(K,L)=Amin(K/a;L/b),
где a,
b
– параметры. параметры характеризуют
удельные затраты капитала и труда,
необходимые для выпуска продукции в
количестве A.
Функция Леонтьева предназначена в
основном для моделирования строго
детерминированных технологий, которые
не допускают отклонения от технологических
норм и нормативов использования ресурсов
на единицу продукции. Как правило, они
используются для формализованного
описания полностью автоматизированных
объектов.Линейная
функция. характерно,
что предельные эффективности
(производительности) по каждому из
ресурсов являются величинами постоянными,
равными по величине коэффициентупри
соответствующем аргументе (ресурсу):
дY/дK=a,
дY/дL=b.
Дост-ва
такой ф-ции состоят, во-первых, в наличии
небольшого числа параметров, имеющих
явный эк. смысл, и, во-вторых, в существовании
производных высших порядков. Кроме
того, степенные производственные ф-ции
с помощью логарифмирования сводятся к
функциям линейным (относительно новых
логарифмических переменных), что удобно
для оценки параметров по статистическим
данным. впервые
были использованы американскими учеными
К. Коббом и П. Дугласом для изучения
связей между национальным доходом и
двумя важнейшими факторами производства
- рабочей силой и основными производственными
фондами. Однако сегодня принято, что
для классической производственной
функции типа Кобба - Дугласа существует
связь между показателями степеней, а
именно α+β=
1.Функция
с фиксированными пропорциями ресурсов
(функция Леонтьева)Эта
функция имеет вид: Y=F(K,L)=Amin(K/a;L/b),
где a,
b
– параметры. параметры характеризуют
удельные затраты капитала и труда,
необходимые для выпуска продукции в
количестве A.
Функция Леонтьева предназначена в
основном для моделирования строго
детерминированных технологий, которые
не допускают отклонения от технологических
норм и нормативов использования ресурсов
на единицу продукции. Как правило, они
используются для формализованного
описания полностью автоматизированных
объектов.Линейная
функция. характерно,
что предельные эффективности
(производительности) по каждому из
ресурсов являются величинами постоянными,
равными по величине коэффициентупри
соответствующем аргументе (ресурсу):
дY/дK=a,
дY/дL=b.
![]()
Линейная функция применяется при моделировании крупномасштабных систем (крупная компания, отрасль, страна), у которой производство продукции есть результат одновременного функционирования большого числа различных технологий.
Производственная функция Алена.
![]()
Функция Алена при положительных коэффициентах b, сиспользуется для формализованного описания производственных процессов, у которых чрезмерный рост одного из ресурсов негативно влияет на объем выпуска продукции. Такая функция применяется для описания мелкомасштабных производственных систем с ограниченными возможностями переработки ресурсов.
Производственная функция CES.Ф-цияCESисп-ся в случае отсутствия точной информации относительно уровня взаимозамещаемости производственных ресурсов, однако имеется основание считать, что уровень производства принципиально не изменится при изменении объемов использования ресурсов. Это характерно для случая, когда экономическая технология имеет свойство определенной устойчивости относительно определенных пропорций ресурсов. Функция используется для моделирования широкого диапазона производственных процессов и имеет вид
![]()
5.
Погрешность аппроксимации функции.Погрешность
аппроксимации представляет собой
отличие опытного значения объема
производства
![]() от теоретического значения, рассчитанного
по одному из уравнений регрессии
от теоретического значения, рассчитанного
по одному из уравнений регрессии
![]() .
Очевидно, чем меньше это отличие, тем
ближе опытные данные к теоретическим
значениям и тем лучше качество модели,
а, следовательно, такую модель целесообразно
рекомендовать к практическому
использованию. Близость опытного и
теоретического значений объема
производства следует устанавливать с
помощью нормы погрешности.
.
Очевидно, чем меньше это отличие, тем
ближе опытные данные к теоретическим
значениям и тем лучше качество модели,
а, следовательно, такую модель целесообразно
рекомендовать к практическому
использованию. Близость опытного и
теоретического значений объема
производства следует устанавливать с
помощью нормы погрешности.
Величина,
представляющая собой разность опытного
и теоретического результативного
признака (![]() –
–![]() )
для каждого опыта представляет собой
погрешность аппроксимации функции
опыта. В данном случае число таких опытов
равно двенадцати. Различают локальную
абсолютную и относительную погрешности.
Кроме того, для оценки погрешности на
всем промежутке изменения ресурсов -
среднюю абсолютную и относительные
погрешности, а также норму погрешности.
)
для каждого опыта представляет собой
погрешность аппроксимации функции
опыта. В данном случае число таких опытов
равно двенадцати. Различают локальную
абсолютную и относительную погрешности.
Кроме того, для оценки погрешности на
всем промежутке изменения ресурсов -
среднюю абсолютную и относительные
погрешности, а также норму погрешности.
Модуль
разность между теоретическим
и опытным
значением результирующего показателя,
вычисленной при конкретном задании
фактора
![]() и
и
![]() ,
называют абсолютной локальной
погрешностью результирующего показателя
и обозначают
,
называют абсолютной локальной
погрешностью результирующего показателя
и обозначают
![]() .
.
Наряду с абсолютной локальной погрешностью рассматривают также относительную локальную погрешность, как отношение абсолютной погрешности к модулю опытного значения результирующего показателя
![]() .
.
Кроме локальной характеристики аппроксимации результирующего показателя рассматривают глобальную характеристику качества аппроксимации, под которой понимается средняя ошибка аппроксимации. Таким образом, для характеристики погрешности на всем промежутке изменения фактора рассматривают среднюю абсолютную и относительную погрешности. Их вычисляют по следующим соотношениям:
![]() и
и
![]() .
.
В качестве нормы погрешности используют следующие:
- равномерная норма как максимальное значение погрешности
![]() или
или
![]() ;
;
- квадратическая норма
![]() или
или
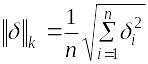 ,
,
![]() ,где
,где
![]()
![]() - количество
опытов.
- количество
опытов.
6. Ф-я предложения по цене.Теория предложения явл зеркальным отражением теории спроса. «Все продавцы будут стремиться получить на рынке самую высокую цену, и чем выше цена, тем активнее будет увеличиваться предложение». Определяющий фактор, влияющий на предложение, явл издержки пр-ва, т.е. сумма денежных расходов на пр-во. Чем ниже издержки, тем по более низким ценам конкурирующие фирмы готовы продавать свои товары.Под предложением понимают совокупность товаров, представленных к продаже по соответствующим, удовлетворяющим товаропроизводителя, ценам.Кривая предложения представляет собой кривую предельных издержек фирмы на пр-во каждой новой единицы продукции.Снижение цены р(х) ведет к соответствующему изменению предложения товаров х, повышение цен ведет к росту предложения.
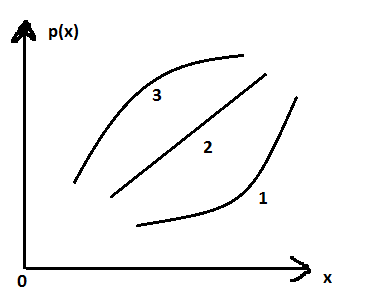
Цена предложения - минимальная предельная цена, по которой фирма, исходя из своих издержек пр-ва еще намерена производить и продавать свою продукцию.
Функция предложения имеет форму: р(х)=с2хβ+с3.
Для кривой 1 – C2>0, C3>0, β>1, x>0, p>0
На величины и знак констант с2 и с3 влияет цена товара, число продавцов, налоги, цены на ресурсы и т.д.
для прямой 2 - C2>0, C3>0, β=1
для кривой 3 - C2>0, C3>0, 0<β<1
Общее св-во: положит знач производной. p’(x), обуловленное положит знач С2 и β
7. Ф-я спроса по цене.Спрос - платежеспособная потребность покупателя, т.е. потребность покупателя, располагающего денежными средствами для приобретения товаров и услуг.
Под потребностью понимается нужда человека в конкретных благах, необходимых для поддержания жизнедеятельности и развития личности.
На спрос влияет 3 фактора: потребность человека в продукте; цена; уровень ден дохода потребителя.
В основе рыночного спроса лежит правило убывающей предельной полезности: «чем выше цена, тем меньше тех, кто согласится купить данный товар, т.е. меньше уровень спроса и наоборот». Напр чем меньше цена жд билета тем больше спрос на него при постояннойпокуп-й способности населения.
График денежного спроса имеет вид убывающей кривой, а ее аналитическое выражение х(р)=с0рα+с1.

Для кривой 1 – C0>0,C1>0,α<0, p (цена)>0, x(спрос) >0
На значения коэффициентов С0 и С1 оказывает влияние число потребителей на рынке, ден доходы и вкусы потребителей, цены конкурентов и цены на замещающие товары и др.
Для прямой 2 - C1>0, C0<0, α=1
Для кривой 3 - C1>0, C0<0,α>0
Общим св-ом для всех кривых явлотрицзнач производной p’(x). Обусловленное для 1 кривой α<0, для ост C0<0.
