Произво́дная

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.

1. Пусть в некоторой окрестности точки 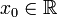  определена функция  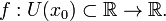Производной функции   в точке   называется предел, если он существует,

• Производная функции в точке   обозначается

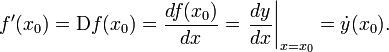
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая  (первая светло серая линия C). Расстояние Δx = x — x₀устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C). Тангенс угла α наклона этой касательной — и есть производная в точкеx₀.

Производные высших порядков.

Правила Лопиталя

Пусть дана функция y=f(x); производная от этой функции y′=f′(x). Производная от этой производной называется производной второго порядка функции y=f(x), которая обозначается как y" или f"(x)= .

Аналогично определяются производные более высокого порядка f ⁽ⁿ⁾(x)= .

Правила Лопиталя

Первое правило. Неопределенность .

Если , то .

Второе правило. Неопределенность .

Если , то .

Неопределенности вида 0∞; ∞-∞; 1^∞;0⁰ сводятся к неопределенностям , путем алгебраических преобразований.

Возрастания убыв

Функция f(x) называется возрастающей в точке х₀, если в некоторой  - окрестности этой точки f(x₀-h)<f(x₀)<f(x₀+h).

Убывающей – если f(x₀+h)<f(x₀)<f(x₀-h), где 0<h<.

Функция f(x) называется возрастающей на отрезке [a,b], если для любых х₁ и х₂ этого отрезка из неравенства х₁>х₂ следует неравенство f(х₁)>f(х₂). Если же из неравенства х₁>х₂ следует, что f(х₁)<f(х₂), то функция f(x) – убывающая на отрезке [a,b].

Функция f(x) может иметь экстремум лишь в тех точках, в которых f'(x)=0 или не существует. Такие точки называются критическими, или стационарными, или подозрительными на экстремум. Равенство нулю первой производной данной функции является необходимым условием существования экстремума.

В качестве достаточного условия существования экстремума в критической точке х₀ можно принять смену знака первой производной при переходе через критическую точку, при этом, если знак меняется с + на -, то в точке х₀ – максимум, если с – на + , то в точке х₀ – минимум.

Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты

Кривая называется выпуклой в точке х=х₀, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой

В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y">0, то кривая вогнутая, если y"<0, то кривая выпуклая.

Точкой перегиба называется точка, разделяющая интервал выпуклости от интервала вогнутости. Необходимым условием существования точки перегиба является равенство нулю второй производной от функции, достаточным – изменение знака второй производной при переходе через точку, подозрительную на точку перегиба.

Существует три вида асимптот: вертикальная, горизонтальная, наклонная.

Пусть y=f(x), а – точка разрыва функции или граничная точка области определения.

Если , то прямая х=а есть вертикальная асимптота.

Если , то прямая х=b – горизонтальная асимптота

Наклонная асимптота имеет вид у=kx+b, где ; .

Алгоритм полного исследования функции y=f(x)

1. Найти область определения функции; точки разрыва.

2. Найти асимптоты графика функции.

3. Определить четность, нечетность, периодичность функции.

4. Установить промежутки возрастания, убывания и экстремумы функции.

5. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции.

6. Найти точки пересечения графика с осями координат.

7. При необходимости вычислить значения функции в дополнительных точках