. Основные элементарные функции, некоторые свойства и графики

Переменная величина у называется функцией переменной величины х, если каждому значению х ставится в соответствие одно определенное значение у.

Х – множество значений переменной х, которое называется областью определения функции и обозначается D(f).

Y – множество значений переменной величины у, обозначаемое как E(f).

Функция   является обратной к функции  , если выполнены следующие тождества:

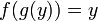•  для всех 

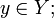
•  для всех 

Пределом числовой последовательности

Число   называется пределом числовой последовательности  , если последовательность  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

Пределы функции

Число А- называется пределом функции у=f(x) в точке х₀,если для любой плоскости допустимых значений аргумента х_n ,nэ N сходящейся к х₀ плоскость соотвтствует значению. А функция сходится к А lim f(x_n)=A.

Пусть функция f(x) определена в некоторой  - окрестности точки а, за исключением, быть может, самой точки а.

Число b называется пределом функции f(x) при ха, если для любого >0 существует число >0, такое, что |f(x)-b|< при 0<|x-a|<.

Предел записывается как 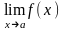=b.

Можно сформулировать следующие свойства пределов:

1. Предел постоянной величины равен самой постоянной величине, то есть , где с – const.

2. Пусть u(x) и v(x) являются функциями аргумента х и их пределы существуют. Тогда .

3. .

4. 

Непрерывность функции

Функция f(x) называется непрерывной в точке а, если она определена в точке а или в некоторой окрестности этой точки и =f(a).

Можно сформулировать четыре условия непрерывности:

1. f(x) должна быть определена в окрестности точки а;

2. должны существовать конечные односторонние пределы и ;

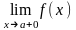3. односторонние пределы должны быть одинаковыми;

4. пределы должны быть равны значению функции в точке а, то есть = =f(a).

Функция f(x) называется непрерывной на отрезке [x₁;x₂], если она непрерывна в каждой внутренней точке отрезка, а на границах выполняются условия: 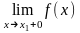=f(x₁), = f(x₂).

Элементарные функции непрерывны во всех точках их области определения.

Разрывы функции

Функция f(x) имеет разрыв в точке а, если она определена слева, и справа от точки а, но в точке а не выполняется хотя бы одно из условий непрерывности.

Различают два основных вида разрыва:

1. Разрывы I рода – а) оба односторонних предела существуют и конечны, но не равны между собой, то есть ≠ . Такой разрыв называется скачком; б) оба односторонних предела существуют, конечны, равны между собой, но не равны значению функции в точке а, то есть = ≠ f(x). Этот предел называется устранимым.

2. Разрыв II рода – хотя бы один из односторонних пределов равен ∞.