§1.1. Матрицы и определители

Матрицей называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрица записывается в виде:

или сокращенно как А=(a_ij), где i=1,2,…,m; i=1,2,…,n.

Матрица, содержащая один столбец или одну строку, называется вектором или вектором-столбцом, вектором-строкой соответственно.

Матрица, у которой число строк равно числу столбцов и равно n, называется квадратной матрицей n-го порядка.

Нулевой называется матрица, все элементы которой равны нулю.

Примеры матриц: а) квадратная; б) диагональная; в) единичная; г) нулевая:

.

Определитель любого порядка можно представить как сумму произведений элементов какого-либо ряда определителя на соответствующие им алгебраические дополнения.

. Обратная матрица. Матричные уравнения и системы линейных уравнений

Обратной матрицей к квадратной матрице А называется такая матрица (обозначается А^-1), что А^-1А=А А^-1=Е.

Замечание. Если матрица А^-1 существует, то она единственна.

Минором М_ij к элементу а_ij квадратной матрицы А называется определитель, вычисленный из элементов матрицы А, оставшихся после вычеркивания i-й строки и j-го столбца.

Алгебраическим дополнением А_ij к элементу а_ij квадратной матрицы А=(a_ij) называется произведение А_ij=(-1)^i+jM_ij.

Присоединенной матрицей к квадратной матрице А=(a_ij) называется матрица , составленная из алгебраических дополнений А_ij к элементам a_ij матрицы А.

Теорема. Если квадратная матрица А – невырожденная (т.е. detA0), то

. (*)

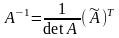Метод присоединенной матрицы вычисления обратной матрицы к невырожденной матрице А состоит в применении формулы (*).

Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом:

АХ=В, ХА=В, АХС=В.

В этих уравнениях А,В,С,Х – матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знака равенства стоят матрицы одинаковых размеров.

Если в этих уравнениях матрицы А и С невырожденные, то их решения записываются следующим образом:

а) для уравнения АХ=ВХ=А^-1В;

б) для уравнения ХА=ВХ=ВА^-1;

в) для уравнения АХС=ВХ=А^-1ВС^-1.

 Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

                      .

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

 

Примеры.

 

1.            2. 

 

Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

Система линейных алгебраических уравнений

Основная статья: Система линейных алгебраических уравнений

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Система m линейных алгебраических уравнений с n неизвестными — это система уравнений вида

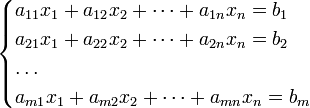
Она может быть представлена в матричной форме как:

или:

.