13.Сформулировать правила действий над векторами в координатной форме.

При сложении 2-х векторов и более их одноименные координаты складываются:

+ =( + ; + );

- =( - ; - );

= ;

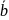Деление отрезков в данном отношении:

Если отрезок MN координаты концов которой известны, точкой К делятся в отношении MK:KN=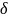 , то координаты точки К вычисляются по формуле:

= ; = ;

Если MK=KN, то = ; = ;

14.Дать определение определителя второго и третьего порядков. Сформулировать свойства и правила их вычисления.

Определителем матрицы 2-го порядка (матрица у которой 2 строки и 2 столбца, квадратная) наз. число равное разности произведений элементов главной и побочной диагоналей.

Определителем 3-го прядка матрицы А наз. число равное сумме произведений элементов главной диагонали и элементов находящихся в вершинах 2-х р/б треугольников с основаниями параллельными главной диагонали и разности произведений элементов побочной диагонали и элементов находящихся в вершинах 2-х р/б треугольников с основаниями параллельными побочной диагонали.

Осн. св-ва определителей:

определитель не измениться, если его строки поменять местами с соот-ми столбцами, транспонировать;

при перестановке 2-х строк или столбцов определитель изменит знак на противоположный;

общий множитель всех элементов строки или столбца можно выносит за знак определителя;

определитель с 2-мя одинаковыми строками или столбцами равен нулю;

если все элементы 2-х строк или столбцов определителя пропорциональны, то определитель равен нулю;

если какой-либо строке или столбцу определителя прибавить соот-е элементы др. строки или столбца, умноженные на одно и то же число, то определитель не изменит своей величины;

треугольный определитель, у которого все элементы, лежащие выше или ниже главной диагонали нули, равен произведению элементов главной диагонали.

15.Дать определение векторного произведения векторов. Вывести формулу вычисления векторного произведения векторов. Сформулировать его свойства и механический смысл.

Векторным произведением * наз. такой 3-й вектор, который определяется след. образом:

модуль вектора равен произведению длин вектора и на sin угла между ними: * * ;

векторы , ориентированы так, что вектор перпендикулярен вектору ;

векторы , после приведения к общему началу ориентированы по отношению друг к другу соот-но как орты , , , т.е. образуют правую тройку.

Формула вычисления векторного произведения векторов:

* = + +

Свойства векторного произведения векторов:

* = ;

* =0, если они каллениарны, если аz, z=0 или b=0;

сочетательное св-во по отношению к скалярному множителю (m* )* = *(m* );

распределительное св-во: *( + )= * + * .

Длина вектора равна площади параллелограмма, построенного на векторах и . В этом и состоит механический смысл (физический).