ф1Дать определение множествф,подмножества и описать действия над ними.

Множество-этосоединение, совокупность,собрание некоторых предметов обьединённых по какому-либо признаку.(множ,букв,алф и т.д.).

Множество В наз. подмножеством множества А,если любой эл-т множества В явл. Эл-том множества А.

Обьединением двух множеств(суммой) наз. Такое множество,к-е сост. Из всех эл-тов данных множеств и только из них,т.е.А U В=С.

Пусть даны 2 множ. А и В, множ,к-е состоит из всех л0тов множ. А не принадлеж. множествут В.наз.разностью множеств А и В.А\В=С.

Прямым произведением множеств А и В наз.множество эл-тами к-го явл. Все упорядоч. Пары (х;у),в к-х 1-м компонентом явл. Эл-т из А,2-м компонентом э-т из множества В.

Множества,между к-ми можно установить взаимно однозначное соответствие наз.эквивалентными или равносильными.

2.Дат определение основных логических операций.Построить таблицы истинности. Использование логических операций при построении электрических схем

Утверждения,для к-х имеет смысл говорить истинны они или ложны, наз.высказыванием

*Операция отрицания(не). Р-высказывание,Р-отрицание.

Отрицанием высказывания Р наз. Такое высказ., к-е истинно, если данное высказывание ложно, и наоборот.

Р	Р
Истинно ложно	Ложно истинно

*коньюнкцией высказывания (и)&(л).коньюнкцией 2-х высказ. Р и q истинно тольков том случае,когда оба высказ. Истинны одновременно.

Р	q	P &q
И И Л Л	И И Л Л	И Л Л Л

*дизъюнкцией (U)2-х высказ. Истинно тогда и только тогда,когда истинно хотя бы одно из высказываний.

Р	q	Pvq
И И Л Л	И Л И Л	И И И Л

*импликация и эквивалентность высказ.(если…то).Импликация 2-ч высказ p&q наз.такое высказ., к-е ложно тогда и только тогда.когда p-истинно,q-ложно(=> -следует)

P	q	P=>q
И И Л Л	И Л И Л	И Л И И

*эквивалентное высказ. Pи q

Наз. Такое высказ. Pq(-следовательно),к-е истинно тогда и только тогда,когда оба высказ. Истинны или ложны одновременно.

p	q	Pq
И И Л Л	И Л И Л	И Л Л И

3.Раскрыть суть метода математической индукции.Формула Бинома Ньютонаи её применение.

Дедуктивный метод-рассуждение от общего к частному.

Индуктивный-от частно к общему.

Простейшим методом рассужд. Явл. Метод инудкции (полной), к-я сводится к рассмотрению каждого из конечных чисел возможных случаев.

Наиболее важным методом доказательства в математике явл. Метод мат. индукции(ММИ),к-й основан на принципе мат.индукции:

Если какое-либо утверждение сформулированное для натурального числа n истинно при n=1 из допущения его истинности при n=k следует его истинность при n=k+1,то утверждение верно для любого натурального n.

Алгоритм ММИ:

1)проверить истинность утверждения при n=1

2)допустить,что выражение истинно при n=k

3)доказать его истинность при n=k+1

Формула Бинома Ньютона

(a+b)ⁿ=C⁰_n*Aⁿ+C¹_n*A^n-1*B+…+C^n-1_n*A*B^n-1+Cⁿ_n*Bⁿ

Треугольник Паскаля:

С₀⁰

С⁰₁ С₁¹

С⁰₂ С¹₂ С²₂

С⁰₃ С¹₃ С²₃ С³₃

…………………..

Примеры:

(a+b)³=a³+3a²b+3ab²+b³

7.

Действия над комплексными числами в тригоном. фор.

Z₁= Z₁ (cos ₁ + i sin ₁)

Z₂=Z₂ (cos ₂ + i sin ₂)

1) Произв. 2-х к 2 в тригоном. форме вычисл по формуле

Z₁Z₂=r₁r₂(cos( ₁+ ₂)+i sin( ₁+ ₂))

2) Частное

(cos( ₁- ₂)+i sin( ₁- ₂))

3) (Z₁)ⁿ=r₁ⁿ(cos( ₁)+i sin( ₁))-Муавра

4) = (cos + I sin ) R=0;1;2…(n-1)

8.cos + i sin = - Эллер

Если к к.ч. модуль кот. =1 поставить в соотв. показат. выраж. , то люб. к ч. можно записать в виде.

r(cos + i sin )=r

1) Z₁Z₂=r₁r₂

2)

3) (Z₁)ⁿ=rⁿ

4) = = i

9. 1.НАЙТИ модуль комп.числа.

2.определить геометрически четверть нахождения точки

3.найти угол из системы

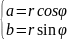
Z=a+bi=2cos +i2sin =2(cos )

10.* Алгебраические многочлены степени n назыв.сумма целых неотрицательных степеней переменной х,взятых с некоторыми числовыми коэфф.,т.е.выраж.вида a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n, a₀≠0

*Теор. Безу-остаток r от деления многочл. F(x) на линейный многочл. Х-с = значению f(c) иногочл. F(x) при х=с,т.е. r=f(c).

*Сформул.правило разлож.многочл.на множ.над полем комплексных чисел Целым рацианальным выраж.или многочл.назыв.выраж.составл.из аргумента и из чисел по средствам только лишь действй(+)или(×).Тождественное преобраз.многочл.х выпол.на основании законов арифм.и вытекающих из этих законов правил действия с любым числом компонента. Сумма всех показателей степени с которыми входят аргументы в одночлен назыв. степенью данного одночлена. Любой многочл.после выполнения надлежащих преобраз.можно представить в виде суммы (Z) не подобных одночл..

Многочл. в таком виде назыв каноническим. Степенью многочл. заданным в каноническом виде назыв.наибольшая из степеней одночленов слогаемых.Канонич.предстовл.многочлен с одним оргументом,принято распологать члены в определённом порядке,оним из 2-х способ.1)По возрастан. степеней a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀; 2)a₀₊ a₁x+a₂x²+a_n-1x^n-1;

11.*Декартовая система коор.-это система координат на плоскости или в пространстве обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осями -прямоугольные декартовые координаты.

*Базисом на плоскости назыв.пара неколениарных вект.взятых в определён.порядке. любой вектор на плоскости может быть представлен единственным способа в линейной комбин.2-х колениар.векторов.

* СФОРМУЛИРОВАТЬ ПРАВИЛА ДЕЙСТВИЙ НАД ВЕКТОРАМИ В ВЕКТОРНАЙ ФОРМЕ???

12.* Линейные операции над векторами назыв.(+,-,×) вектора на число. Суммой вектора a и b назыв.3-й вектор с,начало котор. совпадает с началом вектора а,а конец- с концом вектора b при условии, что вектор b отложен из конца вектора а.Вектор с получается по правилу треуг. Или параллелограмма. Разностью a-b двух векторов a и b назыв.такой век- тор b,который который в сумме с векторам d даёт вектор а: a-b=d, или b+d=a.

*Скалярное произведение 2-х не нулевых векторов назыв. число равное произведению длин и этих векторов на cos угла между ними.

*СФОРМУЛИРОВАТЬ ЕГО СВ-ВА И МЕХАНИЧЕСКИЙ СМЫСЛ?????