Ж##д#дмпы#иоо###рг##уяо##
Для декодирования сообщения заполняются столбцы матрицы. Затем матрица может быть отображена в нормальном порядке.
Для методов перестановки характерны простота алгоритма, возможность программной реализации и низкий уровень защиты, т.к. если криптоаналитик отгадает длину группировки, то затем с помощью ЭВМ может проверить различные перестановки.
Частотный анализ
Большинство естественных языков имеют характерное частотное распределение букв и других знаков. Распределение вероятностей букв:
Английский алфавит Русский алфавит
Е – 0,12 N – 0,072 О – 0,09 Н,Т - 0,053
Т – 0,096 W- 0.02 E – 0,072 Щ,Э – 0,03
А – 0.081 Z - 0.001 А,И – 0,062 Ф - 0,02
О – 0,079
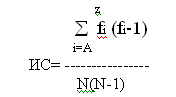Многие сообщения,
зашифрованные методом одноалфавитной
подстановки, сохраняют характерное
частотное распределение и, таким образом,
дают криптоаналитику путь к раскрытию
шифра. Криптоаналитики часто используют
индекс соответствия (ИС) для определения
того, каким методом пользовались при
шифровании исходного текста. ИС
определяется статистически по формуле:
fi - количество i-й буквы в зашифрованном сообщении;
N - общее количество букв в тексте.
В шифрованных сообщениях, у которых ИС большие чем 0.066 (для английского языка), вероятно, применялась одноалфавитная подстановка; если 0.052< ИС <0.066, то, вероятно, был использован двухалфавитный шифр подстановки, 0,047 < ИС < 0,052 был использован 3-х алфавитный шифр. Для многоалфавитной подстановки ИС=0.038, что говорит о равномерном распределении символов и существенно затрудняет раскрытие шифра.
9. Методы шифрования ориентированные на эвм.
Принципиальное значение для надежности шифрования имеет длина кода ключа, т.е. отношение его длины к длине закрываемого им текста. Чем больше оно приближается к единице, тем надежнее шифрование.При этом следует иметь в виду, что это отношение должно распространятся не только на одиночное сообщение, переданное однократно по назначению, но и на все остальные сообщения, закрытые этим же ключом и передаваемые постоянно в течение времени его существования до замены новым значением. Это объясняется тем, что не известен момент возможного подлючения нарушителя к линии связи и поэтому заранее предполагается наихудший вариант, когда нарушитель подключен постоянно. В этом случае при многократном повторении кода ключа по всей длине текста существует опасность его раскрытия статистическим методом.
Для повышения эффективности шифрования используют различные приемы: "длинный" ключ; "двойной" ключ, где два ключа добавляются по модулю два к исходному тексту и другие методы.
1)Применение генератора псевдослучайных чисел. Важно, чтобы ПСЧ были воспроизводимыми. Хорошими показателями обладает линейный генератор ПСЧ, который вырабатывает последовательность ПСЧ Т1,Т2,Т3,...Тm,..., используя соотношение Ti+1=(aT+c) mod m, где а, с - константы; Ti - исходная величина, выбранная в качестве порождающего числа.
Указанное уравнение генерирует ПСЧ с определенным периодом повторения, зависящим от а и с. Значение m обычно устанавливают равным 2 b-1 или 2 b, где b длина машинного слова в битах.
ПСЧ, получаемые по данной формуле, можно использовать как последовательность, из которой выбираются ключи. Каждый ключ затем объединяется обратимым образом с соответствующим объемом текста. Полученный зашифрованный текст достаточно труден для раскрытия, т.к. ключ является переменным. Считается, что если периодичность ключа превышает длину посланного текста и никакой исходный текст не был похищен, то шифр теоретически не раскрываем. Генераторы ПСЧ широко используются для шифрования последовательных файлов и сообщений, передаваемых по линиям связи, а также их применяют для шифрования файлов прямого доступа ограниченных размеров (базы данных).
2)выбор порождающего числа. В генераторе ПСЧ может использоваться пароль пользователя или некоторая его трансформацию в качестве инициирующего порождающего числа. Таким образом, каждый пользователь может иметь свой собственный ключ закрытия секретной информации. Для повышения стойкости шифра последовательность ключа может начинаться не ранее, чем с некоторого фиксированного номера j от начала циклов. Например, если j=8, тогда Т0, основанное на пароле, и Т1,...,Т7 будут генерироваться и отбрасываться, а первым элементом последовательности ключа, реально используемым для шифрования будет Т8.
3)Шифрование файлов произвольного доступа.
В методе Андерсона генерируется две таблицы, каждая равна по длине корню квадратному из количества записей в файле. В этих таблицах содержаться возможные значения Т0 и С. Номер записи преобразуется в два числа, по которым из этих таблиц выбираются Т0 и С для соответствующей записи, обеспечивая уникальную ключевую последовательность для каждой записи. Даже если информация в отдельной записи будет раскрыта, другая запись не будет расшифрована автоматически, т.к. они зашифрованы различными ключевыми последовательностями. Информация внутри самой записи шифруется/дешифруется аналогично последовательным файлам.