Модификации метода Ньютона

Одна из модификаций метода Ньютона заключается в том, что производную от функции f(x) определяют лишь один раз для начальной точки итерационного процесса (рис. 3.5 а):

.

При таком способе решения уравнения скорость сходимости уменьшается, иногда существенно. Эту модификацию метода целесообразно применять в том случае, когда вычисление производной связано с большими затратами вычислительных ресурсов (времени, оперативной памяти), либо когда аналитический вид функции f(x) неизвестен, что часто бывает при решении прикладных инженерных проблем. Кроме того, практически всегда можно подобрать начальное значение таким образом, что , то есть не будет аварийной остановки вычислительного алгоритма.

Другая модификация (метод секущих) заключается в замене производной функции f(x) ее разностным аналогом (рис. 3.5 b):

.

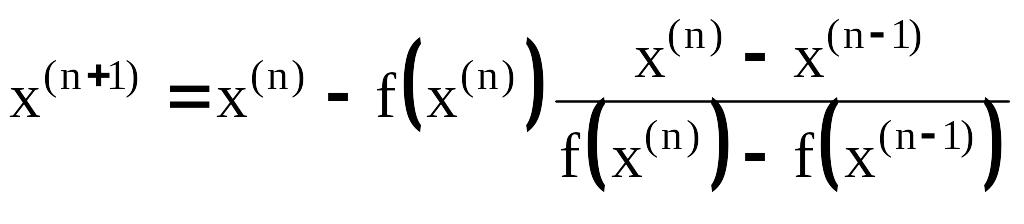В этом случае получена двухточечная схема, то есть для начала расчетов необходимо задать две начальные точки .

Пример 3.3. Определить корни уравнения

.

Точное решение этого уравнения: .

Для использования метода простых итераций представим это уравнение в форме (3.2):

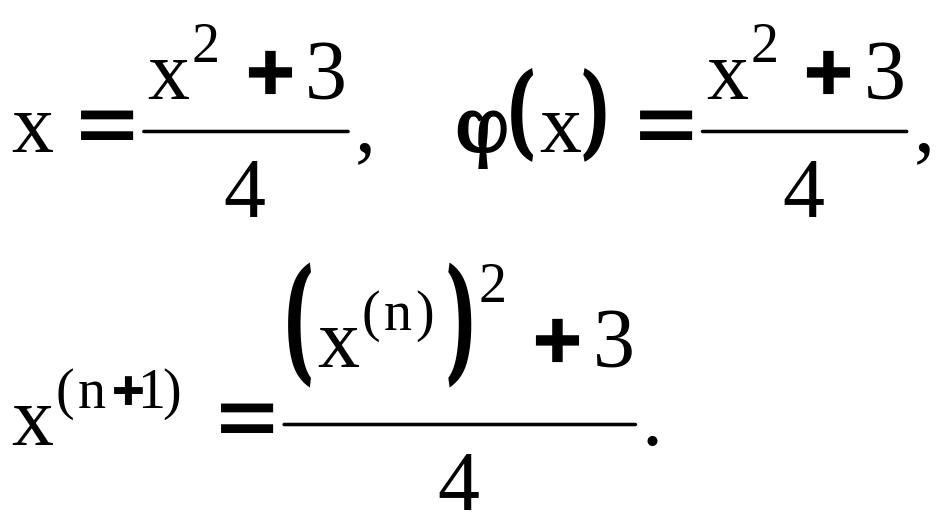
Для проверки условий сходимости в качестве константы условия Липшица возьмем

.

Очевидно, что 0 < C < 1 на интервале (-2, 2), r = 2. Центр интервала a = 0. При этих параметрах условие теоремы

не выполняется, чем объясняется отсутствие сходимости решения, например, при начальном приближении .

Поскольку

,

алгоритм метода Ньютона в соответствии с выражением (3.6) записывается в виде:

.

Результаты вычисления по обоим алгоритмам приведены в табл. 3.3.

x₅ x₄ x₃ x₂ x₁ x₀ x₃ x₂ x₁ x₀ a b

Рис. 3.5. Схемы модифицирования метода Ньютона:

a - с начальным значением касательной; b - метод секущих

Возможно, что на заданном отрезке может оказаться несколько корней. В этом случае итерационный процесс позволит вычислить какой-то один корень уравнения. Для отделения корней в некоторых случаях можно воспользоваться следующим приемом.

Пусть найден корень . Построим функцию

.

Рассмотрим . Вычисление этого предела приводит к неопределенности типа . Согласно правилу Лопиталя [10],

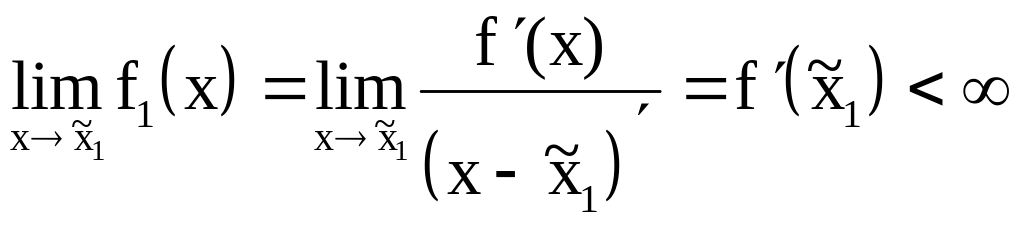
при условии ограниченности производной функции, то есть в случае . При отсутствии кратных корней новая функция и “слева”, и “справа” от точки будет иметь один и тот же знак. После нахождения следующего корня строится функция

,

и так далее.

Таблица 3.3.

10. Методы решения систем нелинейных уравнений: метод простых итераций, методы Ньютона, Якоби и Зейделя. Системы нелинейных уравнений

Рассмотрим систему m нелинейных алгебраических уравнений:

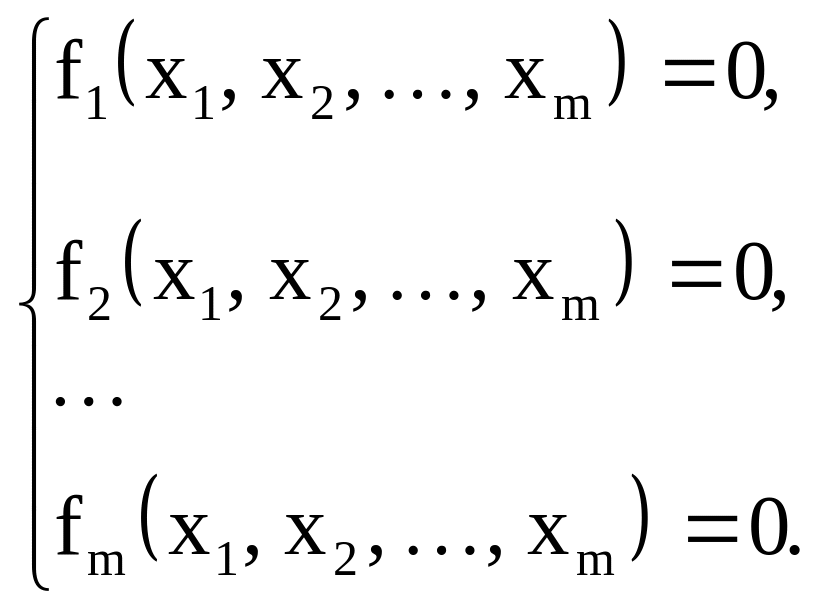
Введем обозначения:

Теперь задача о решении системы нелинейных алгебраических уравнений может быть сформулирована следующим образом: необходимо найти вектор ,

. (3.9)

В общем случае итерационные методы решения системы нелинейных алгебраических уравнений могут быть представлены в канонической форме

, (3.10)

где - начальное приближение; числа и матрицы , имеющие обратные, - итерационные параметры.