4. Прямые методы решения слау: метод квадратного корня. Метод квадратного корня

Метод квадратного корня предназначен для решения систем линейных алгебраических уравнений вида Ax = f с симметричной матрицей коэффициентов .

Метод основан на разложении матрицы коэффициентов А в произведение

, (2.4)

где S - верхняя треугольная матрица с положительными значениями на главной диагонали; D - диагональная матрица со значениями +1 или -1.

Согласно теореме 2.1 при неравенстве нулю всех угловых миноров матрицу А можно разложить в произведение A = LU.

Представим нижнюю треугольную матрицу L с ненулевыми коэффициентами на главной диагонали в виде произведения NK, где N - нижняя треугольная матрица с единицами на главной диагонали, К - диагональная матрица, причем :

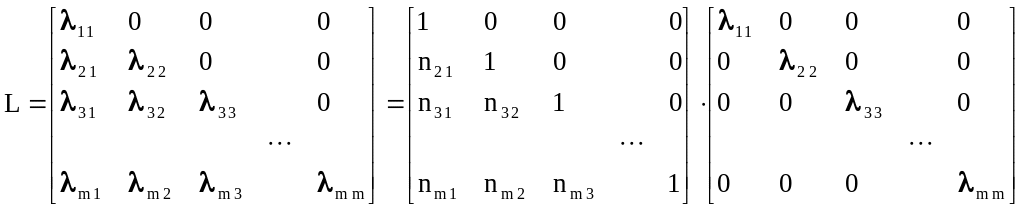
После перемножения матриц N и K получаем систему линейных уравнений относительно величин :

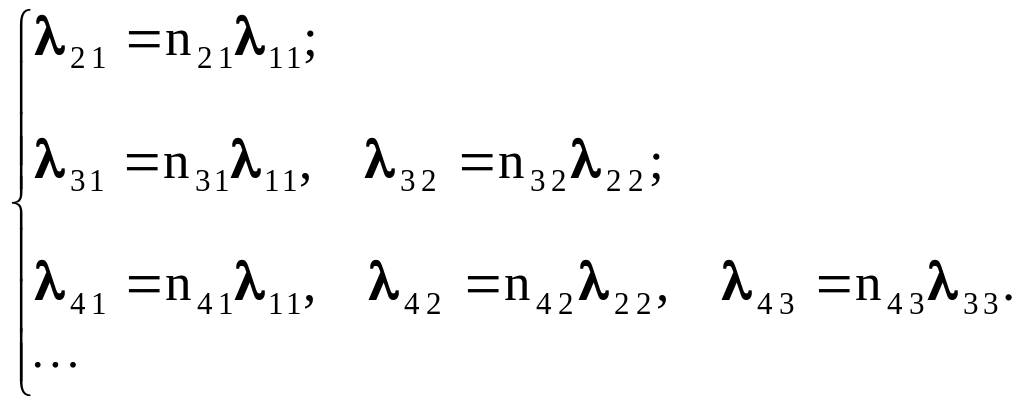
Очевидно, что

, то есть вычисление решения z системы уравнений с нижней треугольной матрицей;

2) Dy = z , вычисление решения системы уравнений с диагональной матрицей;

3) Sx = y , определения из системы уравнений с верхней треугольной матрицей искомого решения.

Построим разложение вида (2.4) для симметричной матрицы третьего ранга:

.

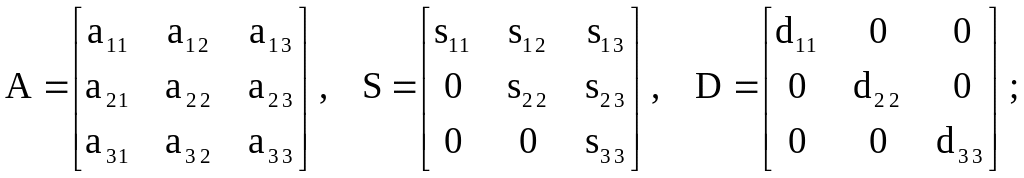
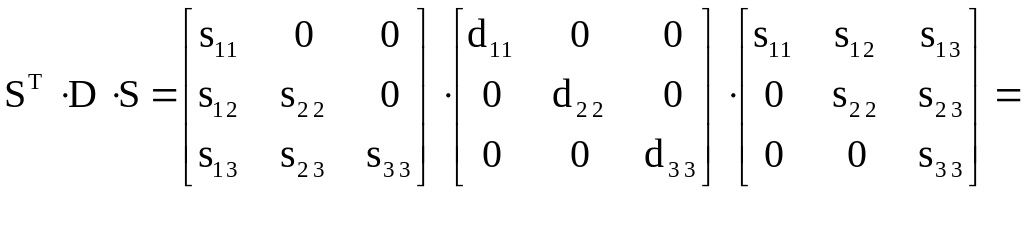
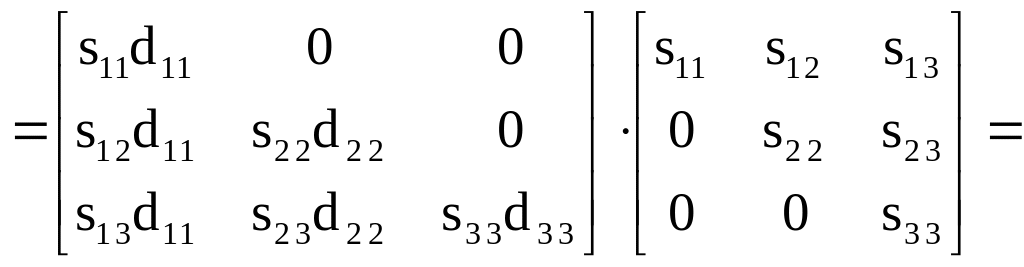
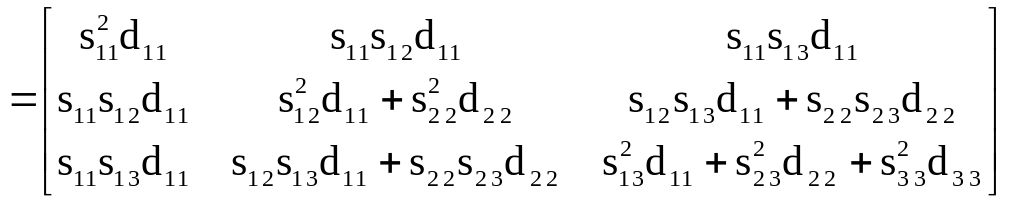Положим , тогда из уравнения получим .

Далее, из уравнения следует, что

.

В силу условия и теоремы 2.2 можно ожидать, что . Аналогично можно вычислить

;

.

Полагая , получим

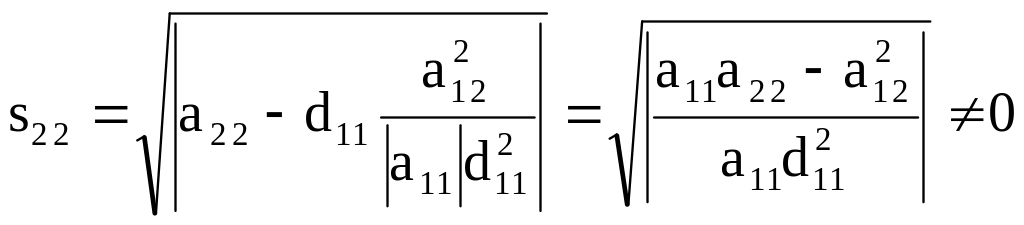
- в силу упомянутого условия .

;

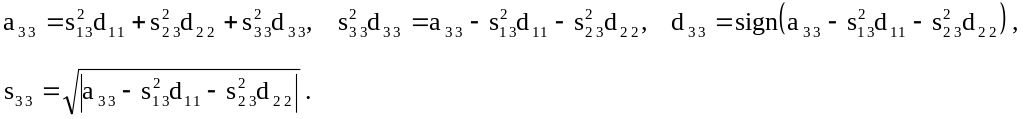
Нетрудно убедиться, что также .

Рассмотрим процедуру построения матриц S и D в случае произвольного числа уравнений m.

Верхняя треугольная матрица по определению имеет нулевые элементы:

. (2.6)

Диагональная матрица D может быть определена формально с использованием символа Кронекера . Теперь можно подсчитать результат перемножения матриц:

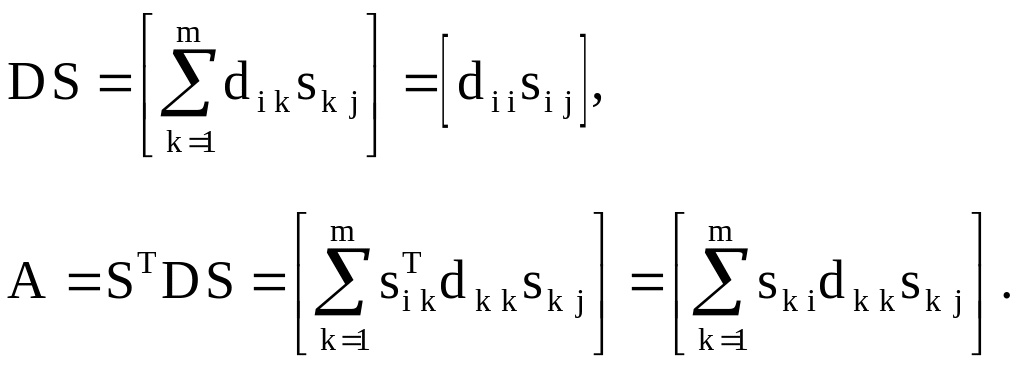
Из последнего выражения с учетом соотношения (2.6) получаем систему алгебраических уравнений:

.

При i = j получаем соотношения для вычисления диагональных значений матриц S и D:

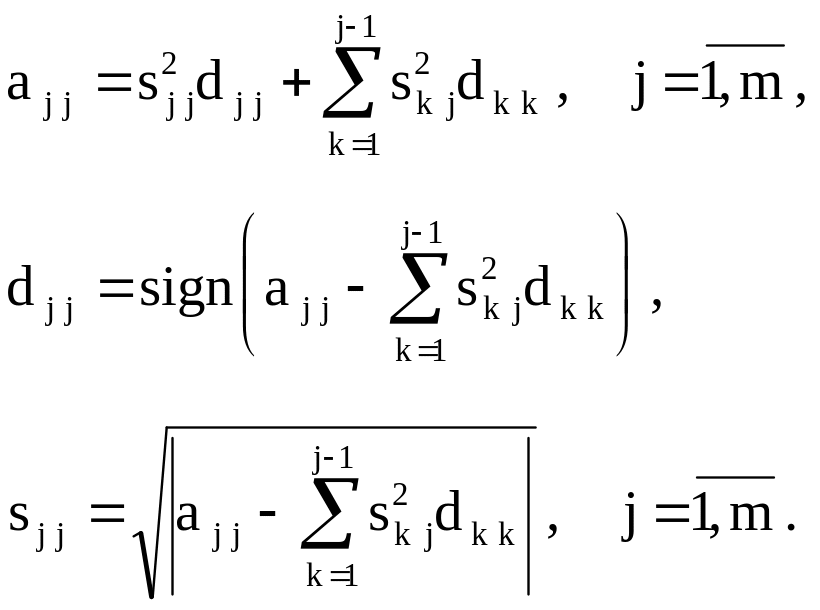
“Наддиагональные” элементы матрицы S определяются по формулам

.

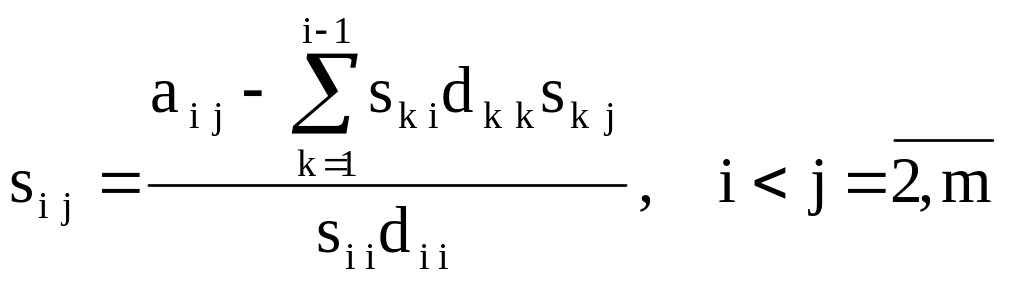Определение числа операций алгоритма метода квадратного корня

Подсчитаем число операций умножения и деления, необходимых для реализации алгоритма метода квадратного корня.

1. Факторизация исходной матрицы, то есть вычисление матриц S и D:

;

2. Выполнение “обратного” хода:

;

3. Вычисление m раз значений квадратных корней.

Общее количество операций равно , или приблизительно , что практически в два раза меньше, чем число операций в алгоритме метода Гаусса.

5. Итерационные методы решения слау: метод Якоби. Метод Якоби

Последнее выражение представим в виде итерационной схемы

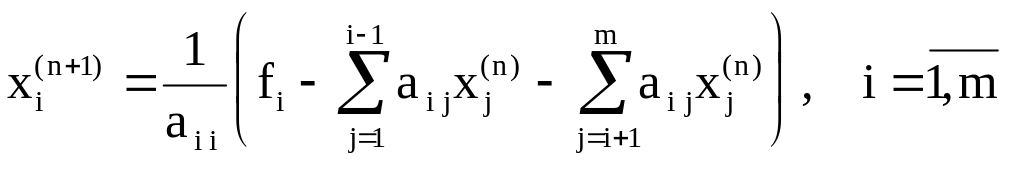, (2.9)

где n - номер итерации. Для получения решения используется следующий алгоритм. В качестве нулевого приближения выбираются какие-либо (зачастую произвольные) значения искомых величин, которые подставляются в правую часть выражения (2.9), что позволяет определить первое приближение неизвестных . Затем полученный результат вновь подставляется в правую часть выражения (2.9) и вычисляются , и так далее. Вычислительный процесс заканчивается, например, когда выполняется условие

,

где  > 0 - заданная точность вычисления результата.

Пример 2.3. Рассмотрим систему алгебраических уравнений

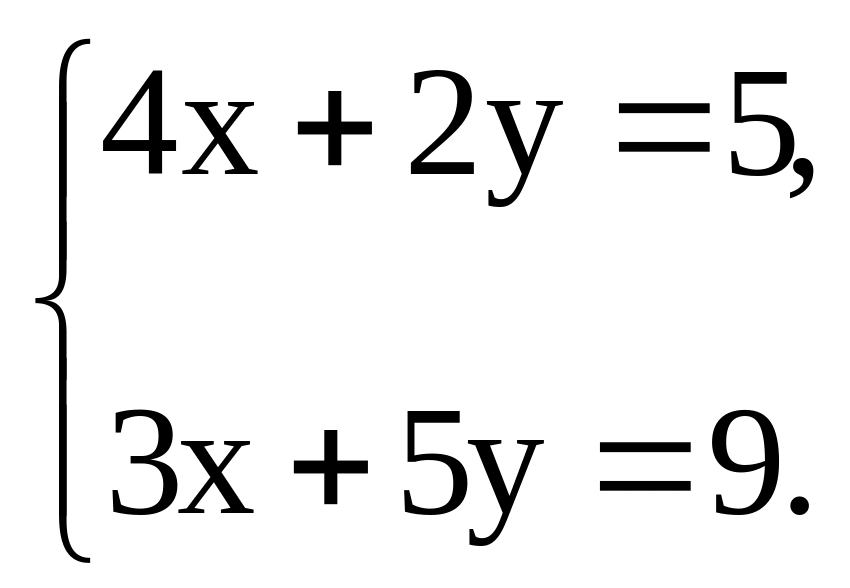
Точное решение этой системы x = 0,5, y=1,5 .

Из первого уравнения выразим первую неизвестную x

,

а из второго - неизвестную y,

.

Представим полученные выражения в виде итерационной схемы

В качестве начального приближения примем . Результаты расчетов сведены в табл. 2.1. На рис. 2.1 графически показан ход выполнения итерационного процесса метода Якоби.

Таблица 2.1

Результаты выполнения итерационной процедуры метода Якоби

n	x(n)	y(n)
0	0	0
1	1,25	1,8
2	0,35	1,05
3	0,725	1,59
4	0,255	1,365
5	0,5675	1,527
6	0,4865	1,4595
7	0,5203	1,5081
8	0,4959	1,4879
9	0,5061	1,5024
10	0,4988	1,4964
11	0,5018	1,5007
12	0,4996	1,4989
13	0,5005	1,5002

Представим матрицу коэффициентов А в виде суммы , где - нижняя треугольная матрица с нулевой диагональю; - верхняя треугольная матрица с нулевой диагональю; - диагональная матрица. Теперь систему уравнений Ax = f можно представить в виде:

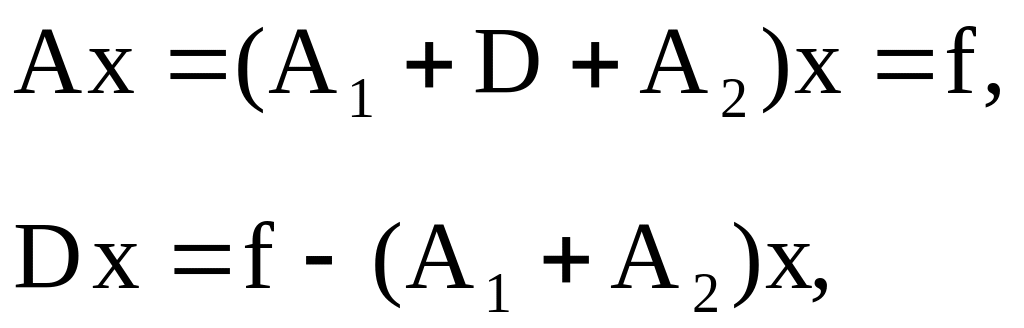
и метод Якоби будет выглядеть следующим образом:

.

Учитывая, что , последнее выражение можно также представить в форме

. (2.10)

Y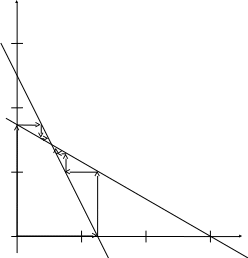

3

4x + 2y = 5

2

1

3x + 5y = 9

0 X

0 1 2 3