Методы решения систем дифференциальных уравнений: метод Эйлера, метод Рунге-Кутты. Метод Эйлера для системы дифференциальных уравнений
Рассмотрим первое уравнение системы (2.18):
.
Разложим решение этого уравнения в ряд
Тэйлора вблизи точки
:
.
Схема Эйлера для этого уравнения принимает вид:
.
Для всей системы уравнений (2.18) схема метода Эйлера выглядит аналогично:
.
Пример 2.7. Решим дифференциальное
уравнение
.
Точным решением уравнения
c заданными начальными условиями является
функция
.
Первая производная решения равна
.
На фазовой плоскости (то есть в системе
координат
)
решение представляет собой окружность
единичного радиуса, поскольку
.
Этот частный факт можно использовать
для оценки погрешности получаемого
численного решения задачи.
Введем обозначения:
.
Теперь исходную задачу можно представить в виде системы дифференциальных уравнений первого порядка с соответсвующими начальными условиями:
,
.
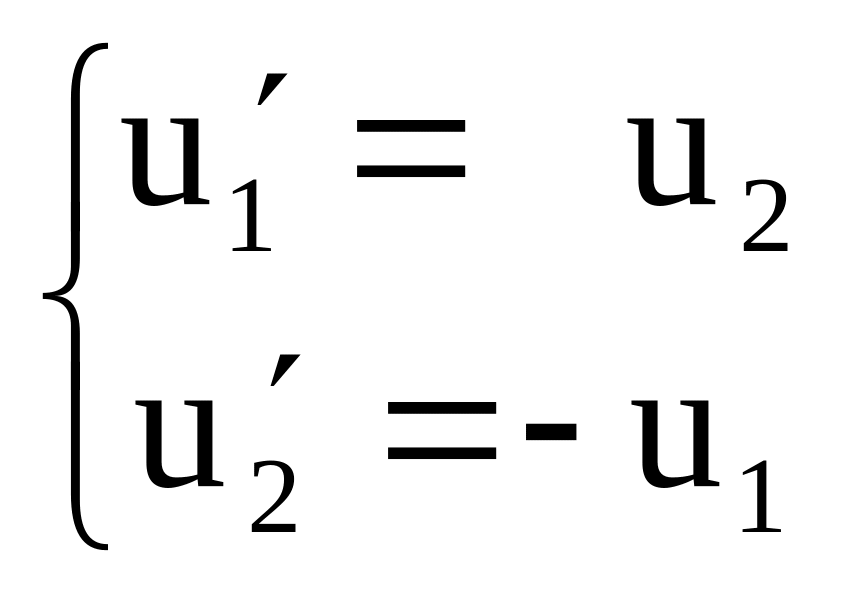Разностная схема для этой системы уравнений записывается следующим образом:
На рис. 2.4 приведен график численного решения y(x), полученный при шаге интегрирования h = 0.1. Поведение полученного решения на фазовой плоскости представлено на рис. 2.5. На рис. 2.6 показана зависимость погрешности численного решения, определяемой как отклонение от единичной окружности, в зависимости от значения аргумента.
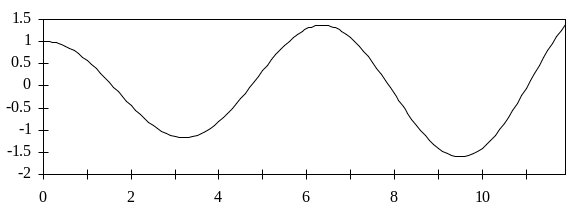
Рис. 2.4. Численное решение методом Эйлера уравнения с шагом интегрирования h = 0.1 .
Метод Рунге-Кутты для системы дифференциальных уравнений
Рассмотрим наиболее распространенную схему четвертого порядка точности.
Введем матрицы
,
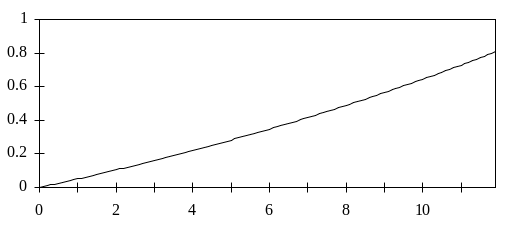
Рис. 2.6. Зависимость отклонения фазовой траектории от единичной окружности в зависимости от значения аргумента
,
,
,
.
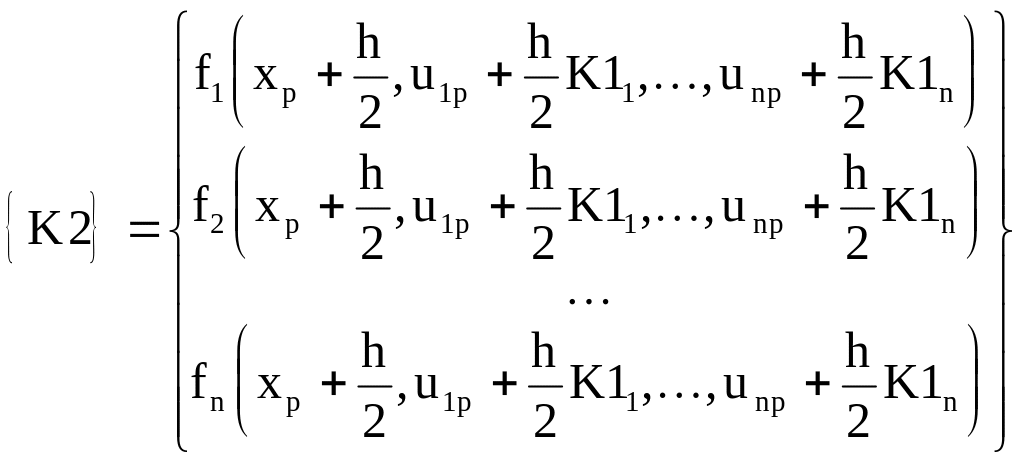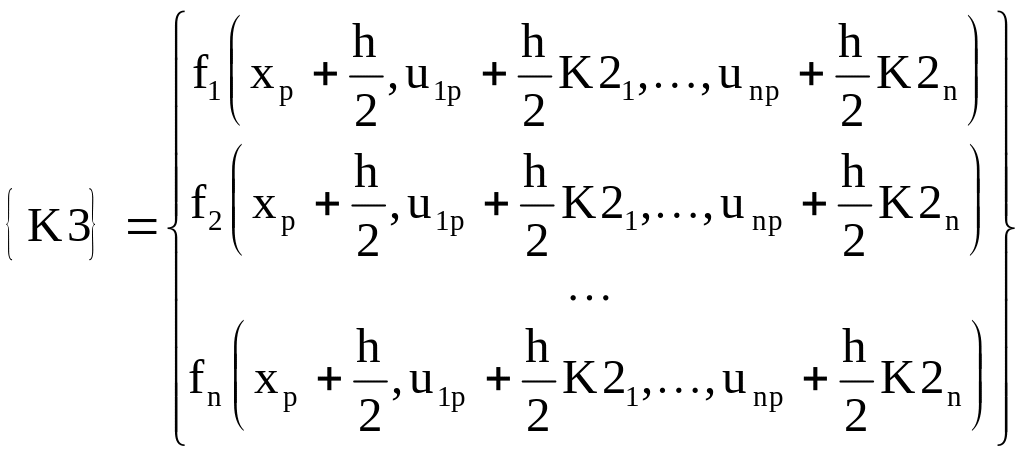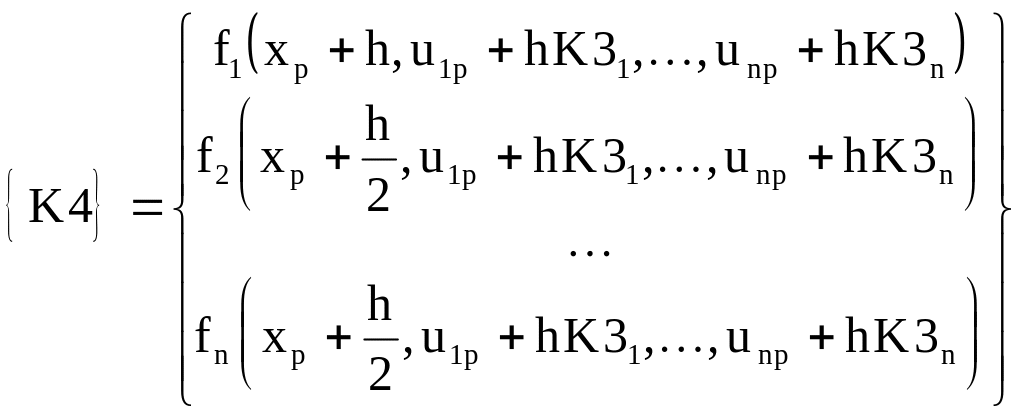Граничная задача. Сеточный метод.
Будем считать, что линейная граничная задача (3.29) - (3.30) имеет единственное решение, непрерывное на отрезке [a, b] вместе с производными до четвертого порядка включительно.
Идея метода сеток заключается в следующем.
1. Область [a, b] задания дифференциального уравнения заменяется дискретной сеточной областью
.
2. Граничная задача (3.29) - (3.30) заменяется сеточной задачей, то есть производные в дифференциальном уравнении заменяются разностными аналогами; в результате этого исходная задача заменяется системой алгебраических уравнений.
3. Решение системы алгебраических уравнений каким-либо численным методом позволяет определить сеточные (узловые) значения искомой функции.
Воспользуемся аппроксимацией первой и второй производных:
,
и запишем разностный аналог дифференциального уравнения (3.29):
. (3.42)
Очевидно, что такие соотношения можно
записать для всех внутренних узлов
сетки
,
то есть для
.
Поскольку в уравнениях (3.42) содержится
(n + 1) неизвестное значение искомой
функции, необходимо дополнить эту
систему еще двумя алгебраическими
уравнениями, получаемыми при замене
граничных условий (3.30) разностными
аналогами:
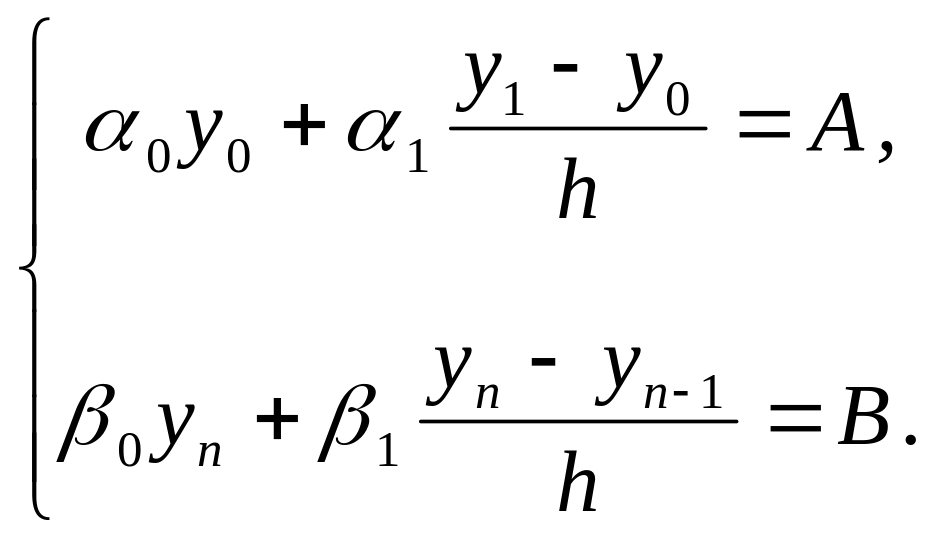(3.43)
Теперь система (n + 1) уравнений содержит ровно (n + 1) неизвестную величину.
Разрешимость системы алгебраических уравнений метода сеток
Для упрощения рассмотрим частный случай
.
Введем обзначения:
,
,
,
.
Теперь задача (3.42) - (3.43) записывается в виде
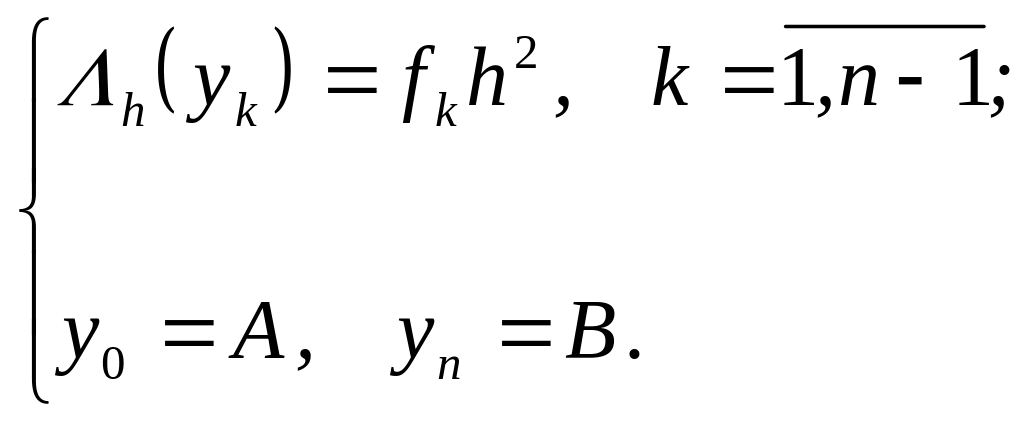(3.44)
Покажем, что соответствующая однородная система алгебраических уравнений
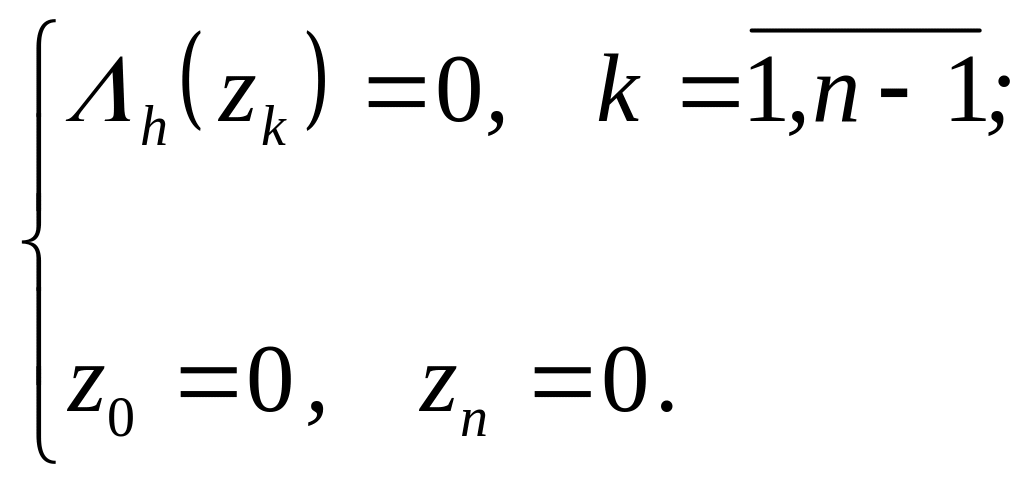(3.45)
имеет только тривиальное решение.
Лемма 3.1. Пусть на отрезке [a, b]
заданы некоторые числа
,
среди которых есть неравные между собой,
и выполнены условия
, (3.46)
а также имеет место
.
Тогда среди чисел
наибольшее положительное значение
принимает либо
,
либо
.
Пусть, напротив, наибольшее положительное
значение
достигается внутри отрезка [a, b]
при некотором значении
,
причем либо
,
либо
.
Тогда в силу условия 1) получим
,
поскольку
.
Благодаря условию 2) имеем:
.
Пришли к противоречию с исходным предположением, что и доказывает лемму.
Лемма 3.2. Пусть на отрезке [a, b] заданы некоторые числа , среди которых есть неравные между собой, выполнены условия (3.46), а также имеет место
.
Тогда среди чисел наименьшее отрицательное значение принимает либо , либо .
Доказательство этого утверждения проводится аналогично предыдущему.
Теорема 3.7. Пусть выполнены условия (3.46). тогда однородная система алгебраических уравнений (3.45) имеет только тривиальное решение.
Доказательство. В соответствии с
формулами (3.45) выполнены условия лемм
3.1 и 3.2 одновременно. В этом случае
наибольшим и наименьшим значениями
являются либо
,
либо
.
Но согласно формуле (3.45)
.
Но это означает, что и все остальные
.
Таким образом, система уравнений (3.45)
имеет только тривиальное решение, и
поэтому ее определитель отличен от
нуля. Следовательно, исходная система
линейных алгебраических уравнений
(3.44) имеет единственное решение.