19. Численное интегрирование: квадратурные формулы прямоугольников, погрешность. Формула прямоугольников

Рассмотрим простейший случай, когда в разложении (7.2) удерживается лишь одно слагаемое, содержащее функцию . В этом случае весовой коэффициент

,

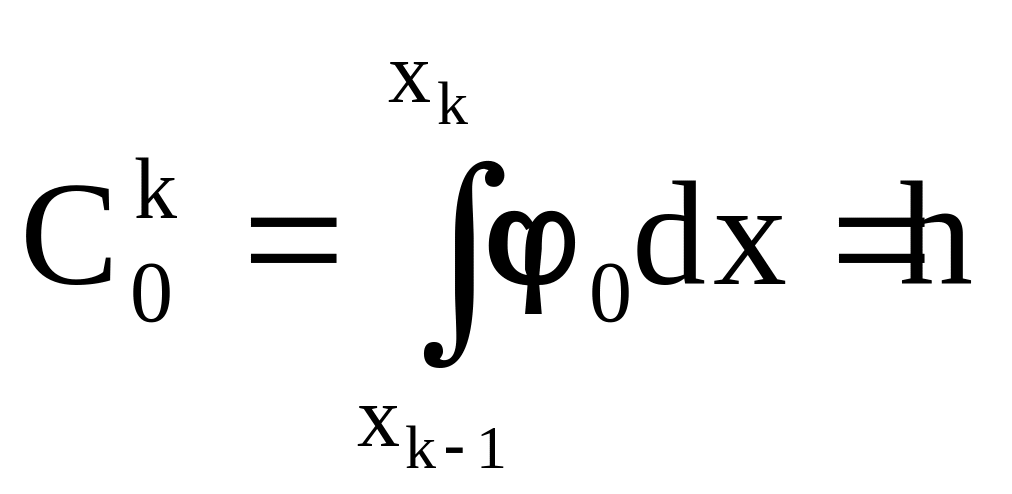и на отрезке интеграл заменяется выражением

. (7.5)

Геометрически это означает замену интеграла на указанном отрезке площадью прямоугольника с основанием h и высотой, равной значению функции в середине основания прямоугольника (рис. 7.1).

x_k-1 x_k-1/2 x_k x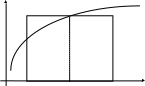

Рис. 7.1. Схема численного интегрирования методом прямоугольников

Воспользуемся для представления функции f(x) вблизи точки формулой Тейлора

.

Определим погрешность вычисления интеграла на отрезке :

.

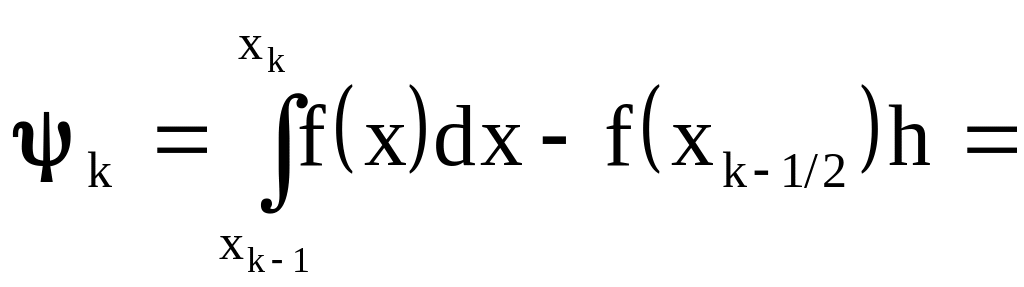
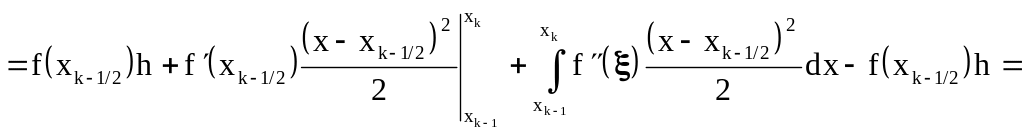
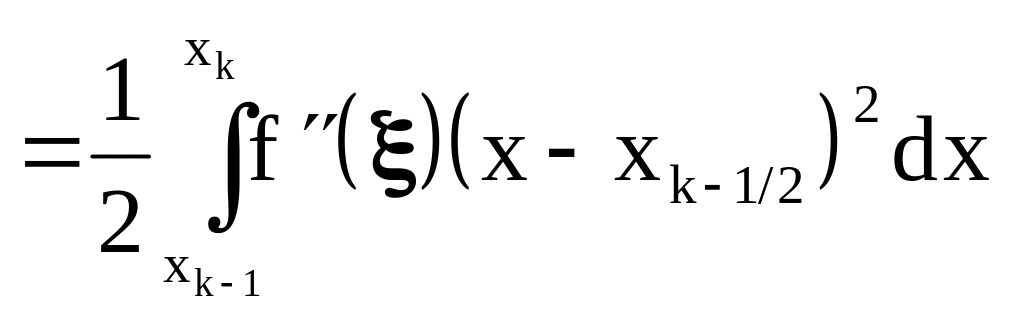Полученное выражение позволяет оценить погрешность:

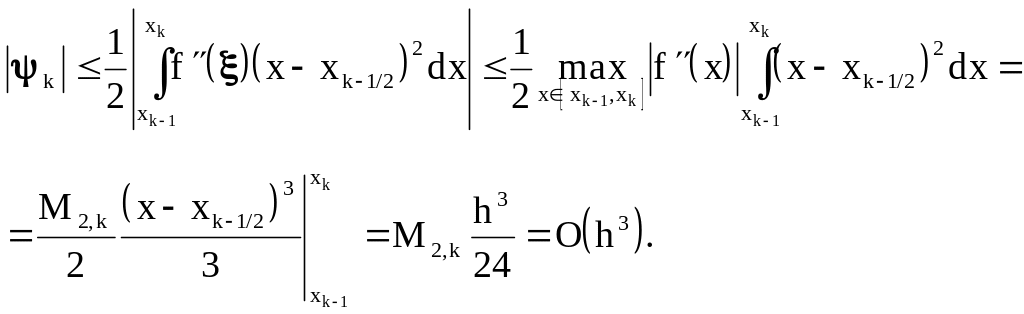(7.6)

Здесь обозначено: .

Формула (7.6) устанавливает, что при ограниченности второй производной на рассматриваемом отрезке погрешность формулы прямоугольников имеет третий порядок. Для всего отрезка интегрирования [a, b] получаем

, (7.7)

где .

Иными словами, для всего интервала [a, b] погрешность рассмотренного способа интегрирования имеет второй порядок.

Аналогичным способом можно проверить также часто применяемую на практике формулу интегрирования

,

геометрический смысл которой пояснен на рисунке 7.2.

Оценка погрешности интегрирования на отрезке , выполненная аналогично предыдущему случаю, приводит к результату

,

.

x_k-1 x_k x

Рис. 7.2. Схема численного интегрирования методом прямоугольников

Для всего интервала [a, b] погрешность интегрирования составляет

.

На рис. 7.3 приведены графики, отражающие сходимость процесса приближенного вычисления определенного интеграла с помощью формул метода прямоугольников с центральной точкой (формула (7.5)), “левой” точкой (рис. 7.2) и “правой” точкой .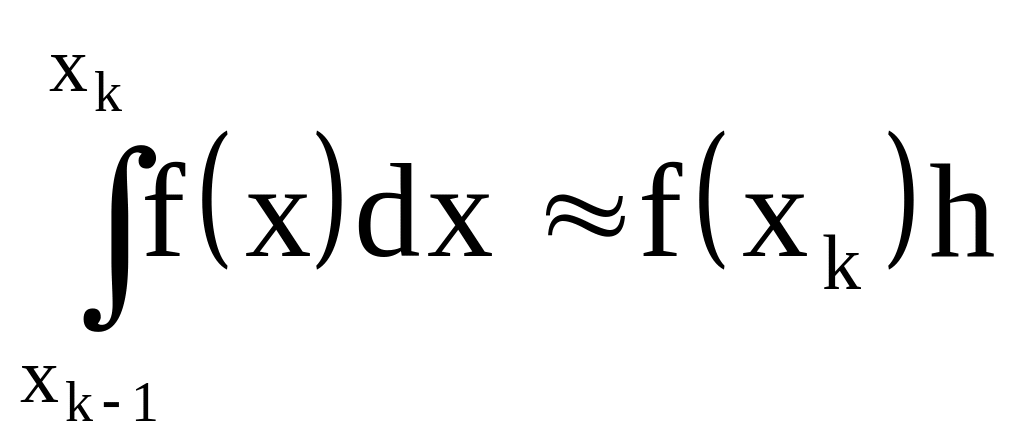

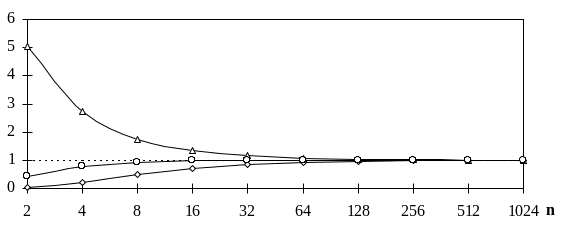
Рис. 7.3. Значения интеграла , вычисленные точно (-------) и по формулам метода прямоугольников с центральной (-  -), “левой” (-  -) и “правой” (-  -) точками на сетках _n

20. Численное интегрирование: формула трапеций, погрешность. Формула трапеций

Заменим функцию f(x) на отрезке линейным приближением

.

Это означает, что в разложении (7.2) удерживаются две функции .

Тогда весовые коэффициенты

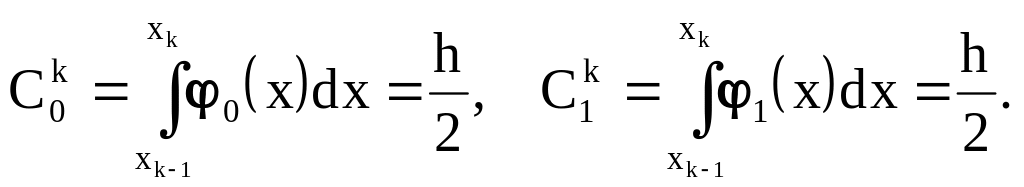
Отсюда вытекает формула метода трапеций (рис. 7.4):

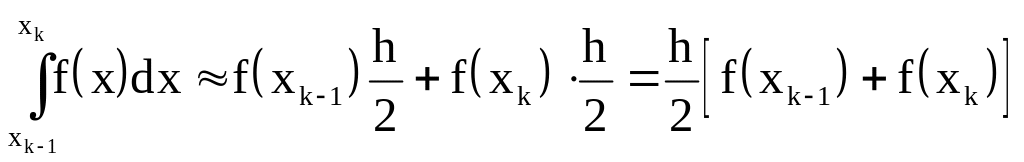. (7.8)

Воспользуемся формулами Тейлора

,

.

x_k-1 x_k x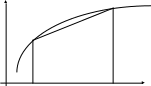

Рис. 7.4. Схема численного интегрирования методом трапеций

Оценим погрешность представления (7.8) на отрезке :

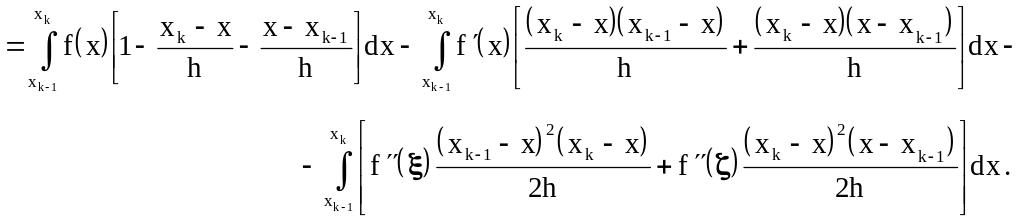
В силу того, что

,

,

вычисляемая погрешность

.

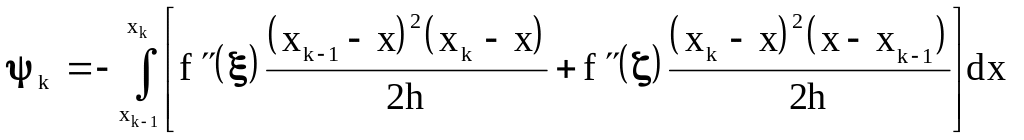Получим оценку погрешности:

.

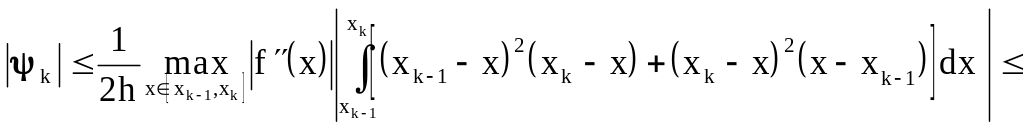
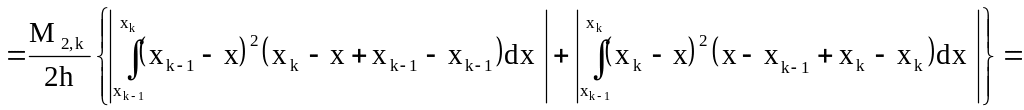
Погрешность для всего отрезка интегрирования [a, b] имеет второй порядок. (7.9)