17. Численное дифференцирование: аппроксимация производных конечными разностями, погрешность. Конечно-разностная аппроксимация

Пусть на отрезке [a, b] введена сетка с шагом ,

.

В произвольной точке этой сетки приближенное значение производной некоторой функции u(x) можно представить несколькими способами:

;

;

.

u(x_i+1)

u(x_i)

u(x_i-1)

x_i-h x_i x_i+h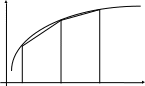

Рис. 6.1. Схема численного дифференцирования

Вполне очевидно, что эти формулы по-разному, то есть с различной степенью точности, представляют значение производной в рассматриваемой точке.

Для оценки получаемых погрешностей воспользуемся разложениями рассматриваемой функции в ряды Тейлора вблизи заданной точки x_i :

,

.

Оценим погрешность представления величиной первой производной, то есть отклонение действительного значения производной от ее приближенного значения:

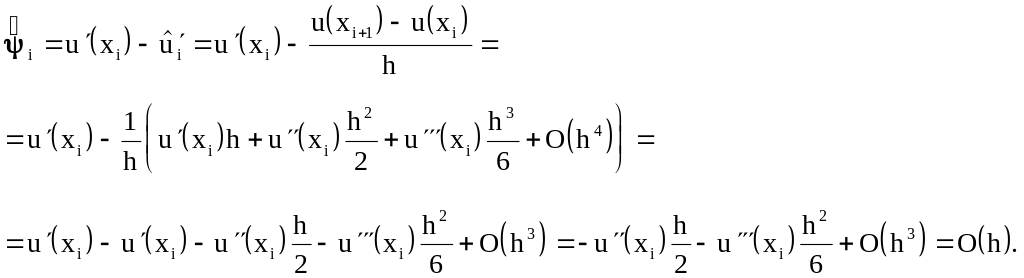
Полученный результат свидетельствует о том, что погрешность аппроксимации первой производной выражением определяется величиной, пропорциональной шагу h сетки при условии ограниченности второй производной и малости самого шага h. В этом случае говорят, что имеет место первый порядок аппроксимации.

Оценим погрешность аппроксимации величиной первой производной:

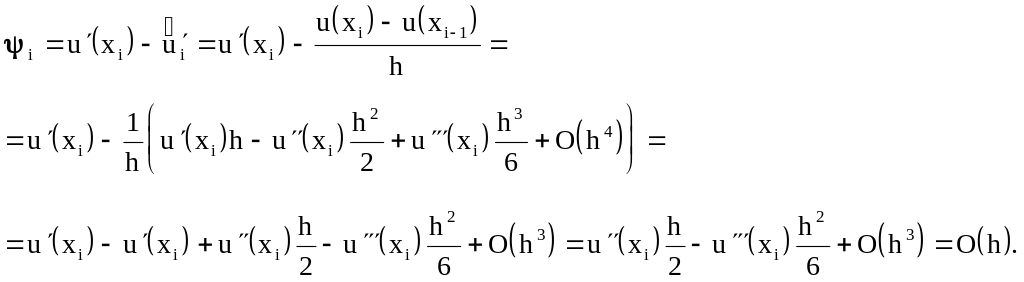
Видно, что в этом случае также имеет место первый порядок аппроксимации.

Аналогично поступим для оценки погрешности формулы :

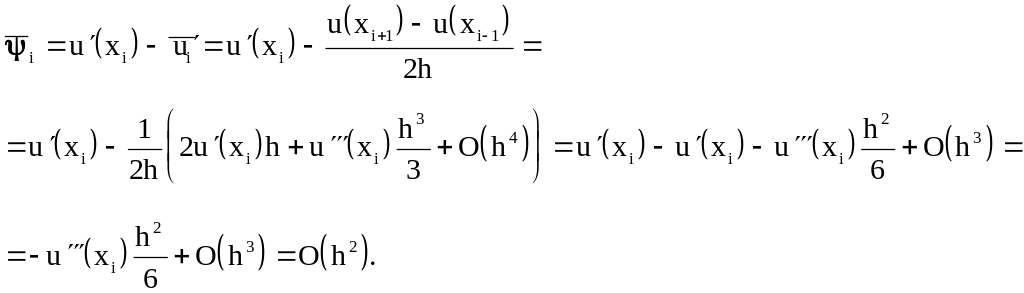
В последнем случае получили уже второй порядок аппроксимации. Это означает, что из трех выражений для аппроксимации производной последний вариант обеспечивает наименьшую погрешность.

Вполне очевидно, что в любом из рассмотренных случаев приближение производной ее разностным аналогом тем точнее, чем меньше шаг h выбранной сетки. Вместе с тем следует иметь в виду, что уменьшение шага h приводит к возрастанию погрешности вычислений.

В самом деле, пусть вместо точных значений и вследствие ошибок округления получены значения и . Аппроксимация производной

вычисляется также с ошибкой . При известных оценках полную погрешность можно также оценить

.

Очевидно, следует потребовать, чтобы погрешность округления не превышала погрешности аппроксимации при записи разностного аналога:

,

где - чебышевская оценка второй производной заданной функции на отрезке [a, b].

Отсюда следует

.

18. Численное дифференцирование: вычисление производных с помощью интерполяционных полиномов.

Для получения приближенного значения производной можно воспользоваться рассмотренными ранее способами аппроксимации значения функции. Идея заключается в том, что сложная функция заменяется вблизи заданной точки некоторым полиномом, для которого и определяется значение производной.

В частности, для трех точек полином Лагранжа имеет вид:

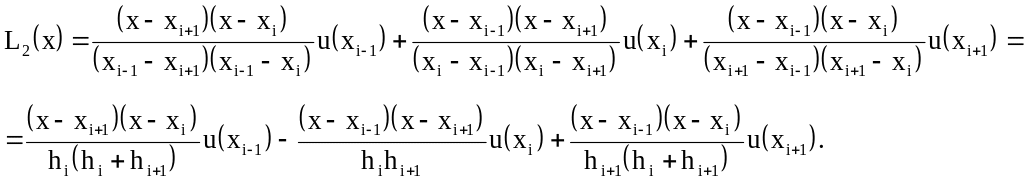
Определим для построенного полинома производные:

,

.

Для выбранной точки получаем значение первой производной

.

Очевидно, что выражение от переменной x не зависит.

В частном случае постоянного шага сетки получаем

,

.