

а б в
Рис. 3.1
![]() (рис.
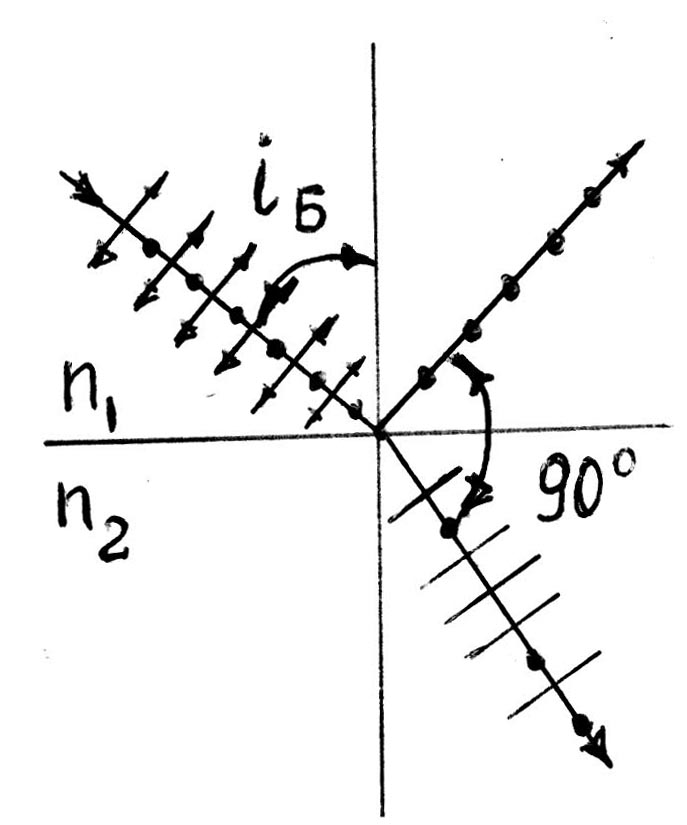
3.1, в). При некотором определенном угле
падения Б
отраженный луч становится полностью
поляризованным. Угол определяется
законом Брюстера: tgБ
=
n21
,где n21
- относительный показатель преломления
вещества. В этом случае угол между
отраженным и преломленным лучами
составляет 900.
При полной поляризации в отраженном
луче
колеблется перпендикулярно к плоскости
падения (плоскость падения - плоскость,
содержащая падающий луч и перпендикуляр
к плоскости диэлектрика в точке падения
луча, рис. 3.2). Преломленный в диэлектрике
луч поляризован частично, в нем преобладают
колебания
,
происходящие в плоскости падения.
Степень поляризации преломленного
луча становится наибольшей при угле
падения, равном углу Брюстера Б.
В этом случае угол между отраженным и
преломленным лучем составляет 90о.
(рис.
3.1, в). При некотором определенном угле
падения Б
отраженный луч становится полностью
поляризованным. Угол определяется
законом Брюстера: tgБ
=
n21
,где n21
- относительный показатель преломления
вещества. В этом случае угол между
отраженным и преломленным лучами
составляет 900.
При полной поляризации в отраженном
луче
колеблется перпендикулярно к плоскости
падения (плоскость падения - плоскость,
содержащая падающий луч и перпендикуляр
к плоскости диэлектрика в точке падения
луча, рис. 3.2). Преломленный в диэлектрике
луч поляризован частично, в нем преобладают
колебания
,
происходящие в плоскости падения.
Степень поляризации преломленного
луча становится наибольшей при угле
падения, равном углу Брюстера Б.
В этом случае угол между отраженным и
преломленным лучем составляет 90о.
 Если
естественный свет падает под углом iБ
на стопу, состоящую из 8–10 прозрачных
диэлектрических пластин (стопу Столетова),
то свет, проходящий через такую стопу
практически полностью поляризован.
Если
естественный свет падает под углом iБ
на стопу, состоящую из 8–10 прозрачных
диэлектрических пластин (стопу Столетова),
то свет, проходящий через такую стопу
практически полностью поляризован.
Рис.
3.2
Проходя через некоторые кристаллы, например, кристаллический исландский шпат (CaCO3), луч света раздваивается. Даже если луч падает на естественную грань такого кристалла нормально, внутри кристалла и на выходе из него в общем случае будет два луча. Такие кристаллы называются двоякопреломляющими. Тот из лучей, для которого выполняется обычный закон преломления, называется обыкновенным лучом (0). Второй луч отклоняется в сторону от направления падающего луча даже при нормальном падении, т.е он не подчиняется закону преломления и называется необыкновенным (е) лучом (рис. 3.3). Показатель преломления необыкновенного луча (в отличие от показателя преломления обыкновенного) зависит от направления его в кристалле. Необыкновенный луч, как правило, не лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности.
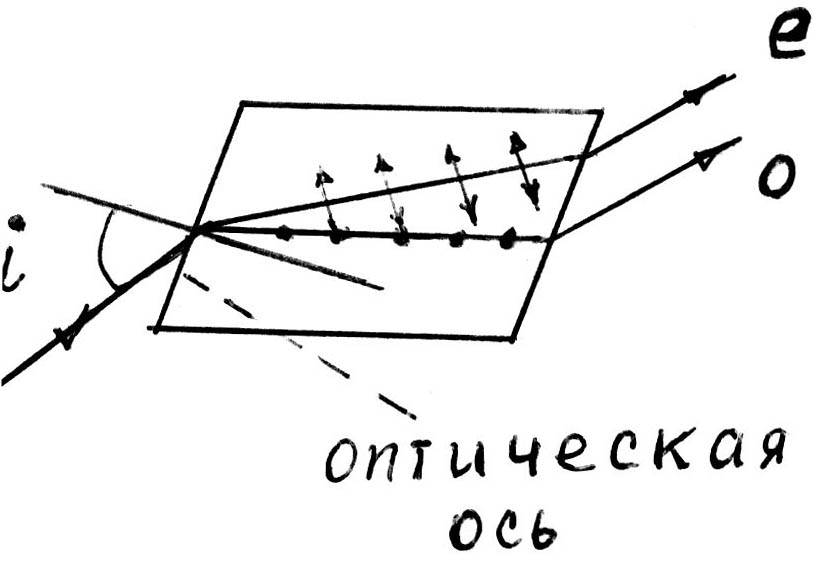
Рис.
3.3
Следует обратить внимание на то, что оптическая ось - не какая-то фиксированная единственная прямая, пересекающая кристалл, а только определенное направление в кристалле. В заданном направлении можно провести через кристалл бесконечно много прямых, которые будут оптическими осями. Плоскость, содержащая луч и оптическую ось, называется главным сечением, или главной плоскостью кристалла.
Обыкновенный луч поляризован таким образом, что вектор колеблется в нем перпендикулярно главному сечению. В необыкновенном же луче вектор колеблется в главной плоскости.
Рис. 3.4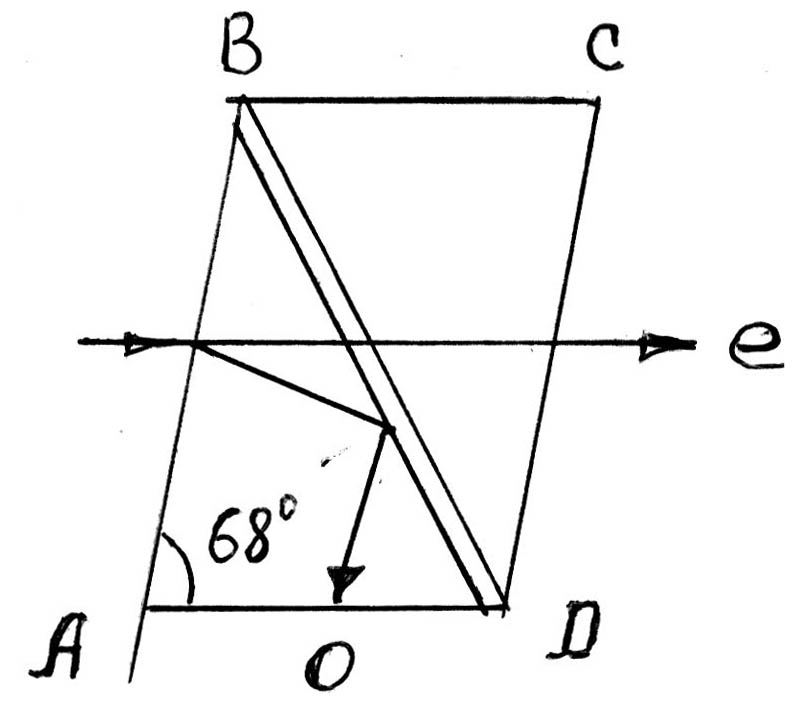
![]() лежит между значениями показателей
преломления обыкновенного
лежит между значениями показателей
преломления обыкновенного
![]() и необыкновенного
и необыкновенного
![]() лучей:
<
лучей:
<![]() <
.
<
.
Две естественные грани АВ и СД кристалла срезают так, что острые углы призмы Николя составляют 68.
Луч, падающий на грань АВ призмы Николя, разделяется на два луча. Обыкновенный луч на границе испанский шпат - бальзам испытывает полное внутреннее отражение и поглощается зачерненной гранью АД. Из призмы выходит. Таким образом, только один плоскополяризованный луч. Плоскость колебаний этого луча называется главной плоскостью призмы.
В некоторых кристаллах (турмалин, геропатит) лучи, поляризованные в разных плоскостях, поглощаются по мере их распространения внутри кристалла неодинаково. Это свойство называется дихроизмом и используется для получения поляризованного света с помощью поляроидов.
Поляроид – тонкая пленка из нитроцеллюлозы, в которую вкраплены мельчайшие кристаллики сильно дихроичного вещества геропатита. Оптические оси этих кристалликов расположены в одном направлении (это достигается специальной обработкой пленки). Свет, прошедший через поляроид, оказывается плоскополяризованным. Прибор, позволяющий получить поляризованный луч, называется поляризатором. Поляризатором может быть стопа Столетова, кристалл турмалина, поляроид, призма Николя. Прибор, позволяющий обнаружить поляризацию света, называется анализатором.
Поляризатор и анализатор взаимозаменимы: один и тот же прибор может быть как поляризатором, так и анализатором.
Интенсивность света, прошедшего через систему поляризатор – анализатор (при отсутствии поглощения в ней), определяется законом Малюса:
![]() ,
(3.1)
,
(3.1)
где
![]() - интенсивность света, прошедшего через
поляризатор;
- угол между главными плоскостями
анализатора и поляризатора.
- интенсивность света, прошедшего через
поляризатор;
- угол между главными плоскостями
анализатора и поляризатора.
Если
на поляризатор падает естественный
свет интенсивностью I0,
то
![]() .
Интенсивность света, прошедшего через
параллельные поляризатор и анализатор
(
= 0), максимальна; скрещенные поляризатор
и анализатор (
= )
свет не пропускают.
.
Интенсивность света, прошедшего через
параллельные поляризатор и анализатор
(
= 0), максимальна; скрещенные поляризатор
и анализатор (
= )
свет не пропускают.
 Соотношение
(3.1) может быть получено следующим
образом. Пусть
Соотношение
(3.1) может быть получено следующим
образом. Пусть
![]() - амплитуда колебаний светового вектора
волны, пропускаемой поляризатором, AA
- главное сечение анализатора. Амплитуду
можно разложить на две взаимно
перпендикулярные составляющие, одна
из которых
- амплитуда колебаний светового вектора
волны, пропускаемой поляризатором, AA
- главное сечение анализатора. Амплитуду
можно разложить на две взаимно
перпендикулярные составляющие, одна
из которых
![]() совпадает с главным сечением анализатора.
Колебания, перпендикулярные направлению
AA,
не проходят через анализатор (рис. 3.5),
поэтому
совпадает с главным сечением анализатора.
Колебания, перпендикулярные направлению
AA,
не проходят через анализатор (рис. 3.5),
поэтому
![]() . (3.2)
. (3.2)
Так как интенсивность световой волны пропорциональна квадрату ее амплитуды, то, возводя правую и левую части уравнения в квадрат, получим закон Малюса:
![]() .
.
При
использовании в качестве поляризатора
и анализатора поляроидов необходимо
учитывать, что поляроиды не обеспечивают
полной поляризации света и неодинаково
прозрачны для лучей разных цветов. В
силу этого интенсивность света, прошедшего
через анализатор, будет складываться
из интенсивности двух лучей: поляризованного
и неполяризованного. Интенсивность
![]() неполяризованного луча не зависит от
угла
между главными сечениями поляризатора
и анализатора. Таким образом, при
использовании поляроидов интенсивность
света, прошедшего через анализатор,
будет определяться соотношением
неполяризованного луча не зависит от
угла
между главными сечениями поляризатора
и анализатора. Таким образом, при
использовании поляроидов интенсивность
света, прошедшего через анализатор,
будет определяться соотношением
![]() . (3.3)
. (3.3)
Лабораторная работа № 3-08
Исследование явления поляризации света
Приборы и принадлежности: оптическая скамья; источник света, подключенный к выпрямителю; выпрямитель, включенный в сеть с напряжением 220 В (позволяет регулировать подаваемое на источник света напряжение и изменять этим его яркость); два поляроида (каждый заключен в оправу с лимбом для отсчета угла поворота поляроида вокруг горизонтальной оси); черное зеркало в оправе, позволяющей поворачивать его вокруг вертикальной оси; фотоэлемент, присоединенный к микроамперметру; штатив с цилиндрическим черным колпачком, в котором закреплен фотоэлемент.
Цель работы: изучение явления поляризации света.
Задание 1. Изучение закона Малюса
В работе в качестве поляризатора и анализатора применяются поляроиды. Поляроиды не обеспечивают полной поляризации света, поэтому закон Малюса имеет вид
![]() ,
,
где
![]() - интенсивность неполяризованного
светового пучка, прошедшего через
систему;
- интенсивность поляризованного
света.
- интенсивность неполяризованного
светового пучка, прошедшего через
систему;
- интенсивность поляризованного
света.
Описание установки и порядок выполнения работы
Схема установки для опытной проверки закона Малюса изображена на рис. 3.6, где 1 - источник света; 2 - поляризатор; 3 - анализатор; 4 - фотоэлемент, являющийся приемником света; 5 - чувствительный микроамперметр для регистрации величины фототока, пропорционального интенсивности света, падающего на фотоэлемент.
У
 становить
приборы на оптической скамье, как
показано на рис. 3.6.
становить
приборы на оптической скамье, как
показано на рис. 3.6.Включить в сеть блок питания источника света.
Включить в сеть блок питания с микроамперметром, к которому подключен фотоэлемент.
Отрегулировать по высоте источник света, поляроиды и фотоэлемент таким образом, чтобы все они располагались на горизонтальной прямой, параллельной оптической оси.
Подобрать подаваемое на источник света напряжение (регулируется ручкой на блоке питания) и пределы измерения микроамперметра (ряд клавиш на нем) так, чтобы стрелка микроамперметра не выходила за пределы шкалы. Расстояние между источником и фотоэлементом должно быть не менее 1 м.
Стрелку на оправе анализатора совместить с нулем шкалы, имеющейся на анализаторе.
Вращая поляризатор, добиться максимальной величины интенсивности света, прошедшего через оба поляроида. Этому соответствует максимальная величина регистрируемого микроамперметром фототока.
Если необходимо, еще раз отрегулировать интенсивность света источника так, чтобы при максимальном отклонении стрелка находилась в пределах последней четверти шкалы микроамперметра.
Поворачивая анализатор в интервале 0 ... 180, через каждые 10 измерять величину фототока. Полученные данные занести в таблицу.
Построить график зависимости фототока I от

Вычислить степень поляризации света, прошедшего через анализатор. Степень поляризации света определяется по выражению
![]() , (3.4)
, (3.4)
где
![]() и
и
![]() - максимальная и минимальная интенсивности
света, соответствующие двум взаимно
перпендикулярным направлениям световых
колебаний в пучке.
- максимальная и минимальная интенсивности
света, соответствующие двум взаимно
перпендикулярным направлениям световых
колебаний в пучке.
Задание 2. Определение показателя преломления диэлектрика по углу Брюстера
При
падении светового луча, распространяющегося
в воздухе, на полированную поверхность
диэлектрика под углом Брюстера
![]() отраженный луч становится полностью
поляризованным. Угол
определяется законом Брюстера
отраженный луч становится полностью
поляризованным. Угол
определяется законом Брюстера
![]() ,
где
,
где
![]() - показатель преломления диэлектрика
относительно воздуха.
- показатель преломления диэлектрика
относительно воздуха.
Порядок выполнения работы
1. Снять анализатор и на его место поставить черное зеркало, которое может вращаться вокруг вертикальной оси.
2. Установить плоскость зеркала перпендикулярно падающему лучу. Установить указатель на лимбе столика за зеркалом на удобной для отсчета отметке (например 0 или 180).
3. Повернуть зеркало на некоторый угол (~40 ... 50) и, вращая поляризатор, визуально наблюдать изображение источника света, даваемое лучами, отраженными от зеркала. Зафиксировать поляризатор в том положении, при котором интенсивность отраженного луча будет минимальной.
4. Вращая зеркало, добиться еще меньшей интенсивности изображения источника. Продолжать поочередное вращение поляризатора и зеркала до тех пор, пока интенсивность отраженного луча не будет уменьшаться. Если на зеркало падает поляризованный свет, то отраженного луча не будет при выполнении двух условий:
1) в падающем свете вектор колеблется в плоскости падения света на зеркало;
2) угол падения равен углу Брюстера.
Поскольку в данной работе в качестве поляризатора используется поляроид, то можно добиться только минимальной интенсивности отраженного луча.
5.
Отметить положение на лимбе указателя
зеркала. Разность между конечным и
начальным значениями углового положения
зеркала будет равна углу
![]() Брюстера.
Брюстера.
6. Используя закон Брюстера, определить показатель преломления стекла, из которого сделано черное зеркало:
![]() .
.
Контрольные вопросы
