7.1.7 Схема замещения фазы асинхронного двигателя

Для расчетов рабочих процессов асинхронного двигателя часто выбирается схема замещения фазы двигателя, состоящая из резистивных и индуктивных элементов с постоянными параметрами, а также резистивного элемента с переменным сопротивлением, замещающим механическую нагрузку на валу двигателя.

Сложность получения такой схемы замещения заключается в том, что, во-первых, неодинаковы частоты токов фаз статора f и ротора f₂ = fs, во-вторых, различны числа витков фазных обмоток статора w₁ и ротора w₂ и их обмоточные коэффициенты k_об1 и к_об2, и в-третьих, различны числа фаз статора m₁ = 3 и короткозамкнутого ротора т₂ = N. Поэтому необходимо все параметры и величины, характеризующие режим фазы ротора, привести к частоте, числу витков, обмоточному коэффициенту и числу фаз статора.

Приведем сначала эти величины к частоте фазы статора. Введем в рассмотрение эквивалентный неподвижный ротор таким образом, чтобы вращающееся магнитное поле двигателя осталось неизменным, соответствующим его рабочему режиму. Неизменность вращающегося магнитного поля означает постоянство энергии, передаваемой от статора к вращающемуся ротору в рабочем режиме или к эквивалентному неподвижному ротору.

Ввиду постоянства вращающегося магнитного поля действующее значение ЭДС в фазной обмотке эквивалентного неподвижного ротора определяется по той же формуле, что и действующее значение ЭДС в фазной обмотке статора в рабочем режиме [см. (7.4,б)], так что с учетом (7.7)

Е_2н = 4,44fw₂k_об2Ф_в = E₂/s, (7.10)

где для короткозамкнутого ротора w₂ = 1/2, k_o62 = 1.

Величина Е_2н называется ЭДС фазы ротора, приведенной к частоте статора. Заметим, что Е_2н является одной из важных расчетных величин для асинхронного двигателя, а ее значение примерно вдвое больше действующего значения ЭДС Е₂, индуктируемой фактически в фазной обмотке заторможенного ротора. Это объясняется тем, что во втором случае увеличивается примерно в 6,5 раза ток в фазной обмотке статора относительно номинального значения, вследствие чего увеличивается падение напряжения Z_об1I₁ на ней и уменьшается намагничивающий ток, возбуждающий вращающееся магнитное поле.

Чтобы вращающееся магнитное поле осталось неизменным при замене вращающегося ротора эквивалентным неподвижным ротором, необходимо, чтобы токи в фазах, имеющие в первом случае частоту f₂ = fs, а во втором — f, были одинаковы по амплитуде и сдвигу фаз относительно возбуждающих токи ЭДС. Это достигается приведением тока фазы вращающегося ротора к частоте f тока неподвижного статора. Ток фазы вращающегося ротора со схемой замещения по рис. 7.11, учитывая (7.10), можно выразить следующим образом:

.

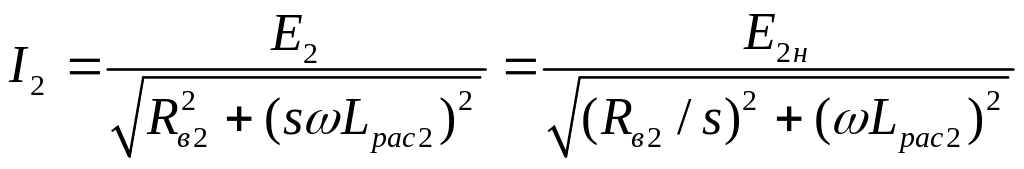Правой части этого равенства соответствует схема замещения фазы эквивалентного неподвижного ротора (рис. 7.13), частота тока в которой равна f, а величина R_в2/s представлена суммой активного сопротивления фазной обмотки ротора R_в2 и некоторого добавочного активного сопротивления R₂(s), во много раз большего, чем R_в2.

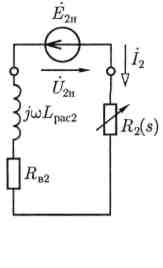
Рис. 7.13

Из сравнения схем замещения фаз вращающегося и эквивалентного неподвижного ротора следует, что ток в каждой из них отстает по фазе от

ЭДС на одинаковый угол

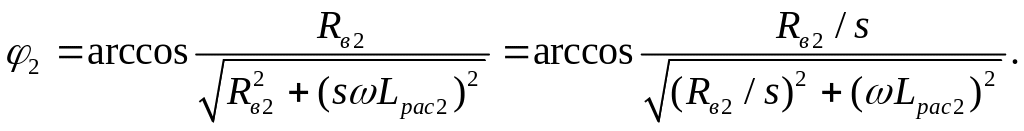
Таким образом, работающий асинхронный двигатель для расчетов может быть заменен эквивалентным неподвижным, в котором цепь каждой фазной обмотки ротора замкнута резистором с сопротивлением

R₂(s) = R_в2(1-s)/s

Мощность этого резистора равна развиваемой механической мощности одной фазы ротора.

Приведем теперь все величины, характеризующие фазу эквивалентного ротора, к числу витков, обмоточному коэффициенту и числу фаз статора подобно тому, как приводились к числу витков первичной обмотки трансформатора величины, относящиеся к его вторичной обмотке (см. 6.2.5).

Электродвижущая сила фазы статора Е₁ связана с ЭДС фазы неподвижного эквивалентного ротора Е_2н соотношением

Е₁ = (w_lk_об1/(w₂k_oб2)E_2н = к_еЕ_2н,

где к_е — коэффициент трансформации напряжений асинхронного двигателя.

Как следует из схемы замещения фазы эквивалентного ротора (рис. 7.13),

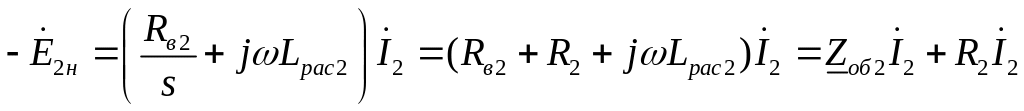
Следовательно,

Ток фазы ротора I₂ можно заменить приведенным током по (7.9):

где k_i — коэффициент трансформации токов асинхронного двигателя.

Сделав подстановку, получим

Произведение k = k_ek_i — это коэффициент трансформации асинхронного двигателя.

Введем теперь в уравнения электрического состояния фазы статора асинхронного двигателя приведенные сопротивления цепи эквивалентного ротора:

и (7.11)

Элементы с такими сопротивлениями в цепи фазы статора будут потреблять такую же энергию и при том же сдвиге фаз между напряжением и током, как это имеет место в соответствующих сопротивлениях элементов цепи фазы ротора (см. рис. 7.13).

Таким образом, ЭДС фазы статора

а напряжение статора (фазное)

(7.12,а)

С другой стороны, ЭДС пропорциональна намагничивающему току I_1х и по тем же соображениям, как и для трансформатора,

где условная величина , модуль которой имеет размерности сопротивления, в схеме замещения соответствует магнитной цепи двигателя. Следовательно, для напряжения фазы статора справедливо также уравнение

(7.12,б)

Вместе с уравнением тока статора

(7.13)

два уравнения напряжения фазы статора (7.12) можно рассматривать как уравнения, соответствующие законам Кирхгофа для цепи со схемой замещения по рис. 7.14,а. В ней элементы изображают схему замещения обмотки фазы статора, — обмотки фазы ротора, Z₁₂ — магнитную цепь машины, a R'₂ = R'_в2(1 — s)/s — механическую нагрузку.

При синхронной частоте вращения (s = 0) сопротивление резистивного элемента, соответствующего механической нагрузке в эквивалентной схеме замещения,

R'₂ = R'_в2/s - R'_в2 = R'_в2(1 - s)/s = ∞.

Если затормозить двигатель до полной остановки (s = 1), то R'₂ = 0.

По этой причине опыт полной остановки двигателя именуется опытом короткого замыкания — обычно он осуществляется при сильно пониженном напряжении на статоре.

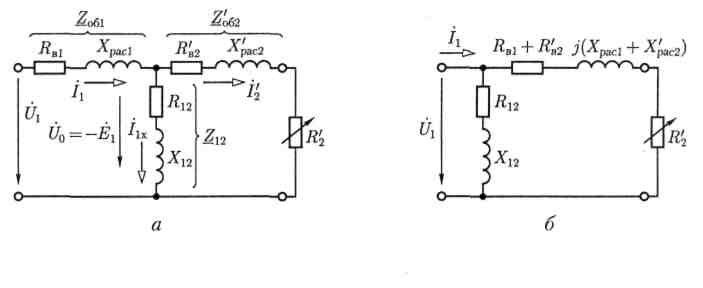
Рис. 7.14

На рис. 7.14, б изображена упрощенная Г-образная схема замещения одной фазы асинхронной машины, составленная в предположении, что

U₀ U₁