2.7. Метод эквивалентного преобразования схем

В ряде случаев расчет сложной электрической цепи упрощается, если в ее схеме замещения заменить группу резистивных элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится.

2.7.1 Смешанное соединение резистивных элементов

При наличии в цепи одного источника внешнюю по отношению к нему часть схемы можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение резистивных элементов.

Для расчета такой цепи удобно преобразовать ее схему замещения в эквивалентную схему с последовательным соединением резистивных элементов. Например, в цепи на рис. 2.11,а между узлами а и b включены три резистивных элемента с сопротивлениями R₂, R₃ и R₄, т.е. проводимостями

G₂ = 1/R₂, G₃ = I/R₃, G₄ = 1/R₄; эквивалентная проводимость

G_э = 1/R₂ + 1/R₃ + 1/ R₄ (2.12)

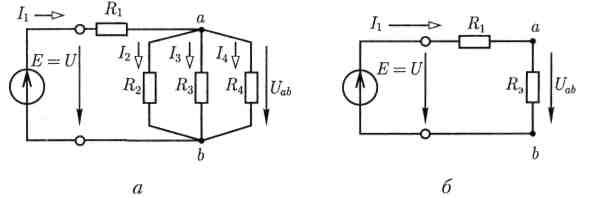
Рис.2.11

После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением R_э = 1/G₃ получается эквивалентная схема с последовательным соединением двух резистивных элементов R₁ и R_э (рис.2.11,б).

Ток в неразветвленной части

I₁ = U/( R₁ + R_э), и токи в параллельных ветвях

I₂ = U_ab/R₂; I₃ = U_ab/R₃; I₄ = U_ab/R₄, (2.13)

где U_ab = R_э I₁

2.8.2. Соединение резистивных элементов по схеме

звезды и треугольника

В общем случае схему замещения цепи по схеме n-лучевой звезды из резистивных элементов можно заменить эквивалентной схемой в виде

n-стороннего многоугольника. Обратное преобразование возможно в ограниченном числе случаев. В частности, преобразования в обоих направлениях возможны для случая треугольника и трехлучевой звезды. Такое преобразование применяется при расчетах сложных цепей постоянного тока и цепей трехфазного тока.

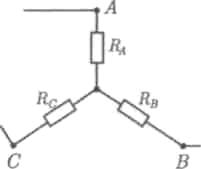
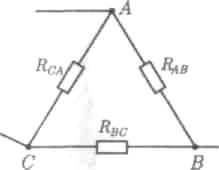
Эквивалентность схем в виде треугольника и звезды (рис. 2.12) получается приравниванием значений сопротивлений или проводимостей между одноименными узлами этих схем, отсоединенных от остальной части цепи.

Найдем сопротивление между узлами А и В.

Проводимость между узлами А и В для схемы треугольника на

рис. 2.12,а

,

Сопротивление между узлами А и В – величина обратная проводимости между этими узлами, т.е.

.

Для схемы на рис.2.12,б сопротивления между этими же узлами А и В равно сумме сопротивлений двух ветвей: R_A+R_B.

Согласно условию эквивалентности должно выполняться равенство

; (2.14)

здесь - сумма сопротивлений всех ветвей для треугольника.

а б

Рис.2.12

Структуры треугольника и звезды по отношению к узлам сим­метричны. Поэтому уравнения равенства сопротивлений между узлами В и С и между узлами С и А можно получить из (2.14) простой циклической перестановкой индексов:

; (2.15)

; (2.16)

Чтобы определить сопротивление R_A звезды, сложим (2.14) и (2.16) и вычтем из этой суммы (2.15); разделив полученное на 2, найдем

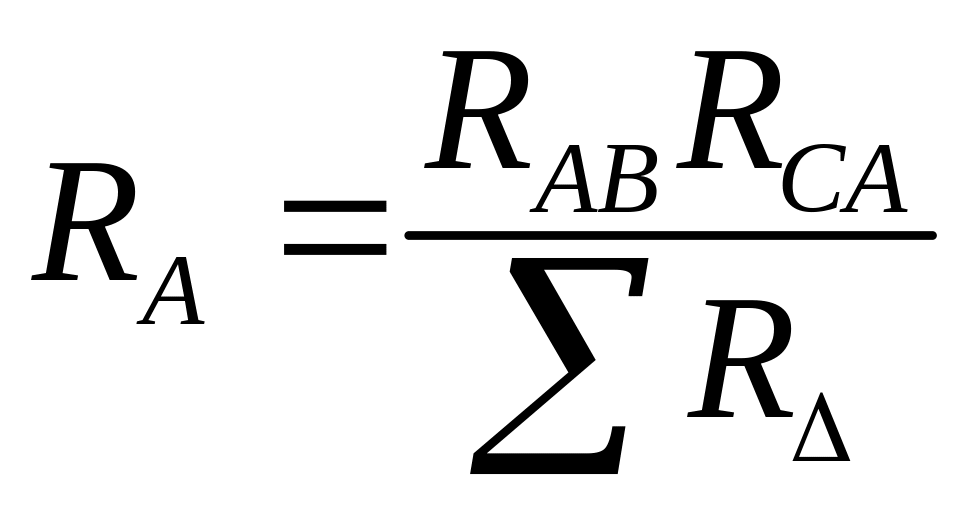(2.17)

Сопротивления других ветвей звезды получим путем циклической перестановки индексом:

(2.18)

(2.19)

В случае равенства сопротивлений ветвей треугольника (R_AB=R_BC=R_CA= ) сопротивление ветвей эквивалентной звезды тоже одинаковы:

(2.20)

Возможно обратное преобразование звезды из резистивных элементов в эквивалентный треугольник.

Для этого перемножим попарно выражения (2.17) — (2.19) и сложим полученные произведения:

.

Последнее уравнение разделим на (2.19) и определим сопротивление ветви треугольника:

(2.21)

Путем циклической перестановки индексов в (2.20) найдем выражения для сопротивлений двух других ветвей:

(2.22)

(2.23)