6.2.3. Уравнения идеализированного однофазного трансформатора

Рассмотрим сначала идеализированный однофазный трансформатор с магнитопроводом, выполненным из ферромагнитного материала с линейной зависимостью индукции от напряженности магнитного поля В = µ_r µ₀ Н (см. рис. 6.5, в).

В 6.1.3 отмечалось, что магнитное поле в магнитопроводе с площадью поперечного сечения S неоднородное. Для упрощения расчетов не будем учитывать неоднородность поля и примем, что индукция и напряженность определяются их значениями на средней магнитной линии длиной l_ср.

Электрическая цепь трансформатора с таким магнитопроводом линейная. Следовательно, для ее анализа можно пользоваться комплексным методом.

На рис. 6.12 приведена схема включения идеализированного однофазного трансформатора между источником ЭДС Е и приемником с комплексным сопротивлением нагрузки .

Рис. 6.12

Запишем значения ЭДС и , индуктируемых в первичной и вторичной обмотках идеализированного трансформатора магнитным потоком Ф в магнитопроводе. По закону электромагнитной индукции в комплексной форме:

(6.4,a)

(6.4,б)

где и — комплексные значения индукции и напряженности маг­нитного поля.

При комплексных токах в первичной и вторичной обмотках идеализированного однофазного трансформатора и напряженность магнитного поля на средней линии магнитопровода по (6.2)

(6.5)

По определению ЭДС источника ,a ЭДС в обмотках идеа­лизированного трансформатора по второму закону Кирхгофа для контуров, отмеченных на рис. 6.12 штриховой линией, и . Поэтому с учетом (6.4) и (6.5)

(6.6,а)

(6.6,б)

В частности, в режиме холостого хода трансформатора (цепь вторичной обмотки разомкнута и ток = 0)

(6.6,b)

где — ток холостого хода, или намагничивающий ток.

Действующее значение напряжения в соответствии с (6.6,а) может быть выражено:

(6.7)

Так как ЭДС источника является заданной величиной, то по (6.6,а) и (6.6,в)

(6.8)

Поделив почленно (6.6,б) на (6.6,а), получим

U₂/U₁=w₂/w₁=n₂₁ (6.9)

—коэффициент трансформации идеализированного однофазного трансформатора, а подставив комплексное значение магнитного потока Ф в магнитопроводе из (6.6,б) в (6.6,а), получим

(6.10)

Преобразуем выражение (6.10), умножив и разделив его правую часть на w₁/w₂:

(6.11)

где

(6.12)

—комплексное сопротивление вторичной цепи, приведенное к первичной, или приведенное сопротивление;

(6.13)

—комплексный ток вторичной цепи, приведенный к первичной цепи, или приведенный ток.

Пользуясь понятиями приведенных тока и сопротивления, представим уравнения (6.6) и (6.8) в следующей форме:

(6.14,а)

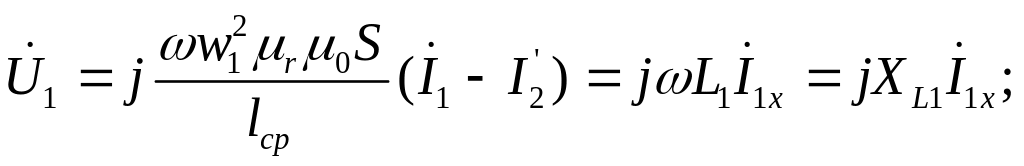(6.14,б)

, (6.14,в)

где - индуктивность первичной обмотки идеализированного однофазного трансформатора; — комплексное напряжение вторичной цепи идеализированного однофазного трансформатора, приведенное к первичной цепи, или приведенное напряжение.

Уравнениям (6.14) соответствует схема замещения цепи, изображенная на рис. 6.13, на которой схема замещения идеализированного трансформатора обведена штриховой линией. Если относительная проницаемость материала магнитопровода , то индуктивное сопротивление X_L1 становится бесконечно большим, а ток намагничивания I_1х = 0. Идеализированный трансформатор с таким магнитопроводом называется идеальным. С помощью такого трансформатора можно реализовать передачу приёмнику максимальной энергии.

Рис. 6.13