3.9.2. Резонанс токов.

В участке цепи, схема замещения которой содержит параллельно соединенные индуктивный, емкостный и резистивный элементы (рис. 3.16), может возникнуть резонанс токов.

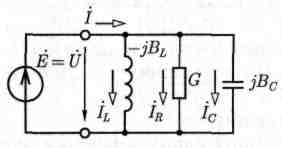
Рис.3.16

При заданном напряжении питания комплексное значение общего тока

,

где

и

—комплексная и полная проводимости цепи; 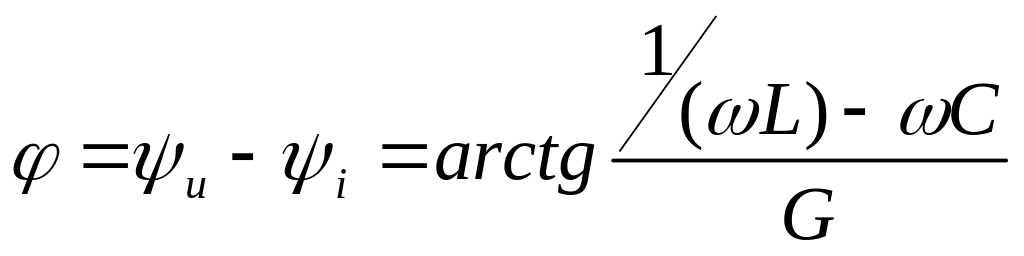- угол сдвига фаз между напряжением и общим током, т.е. аргумент комплексной проводимости.

Действующее значение тока

.

При угловой частоте индуктивная B_L = 1/(ωL) и емкостная В_с = ωС проводимости параллельных ветвей одинаковые, аргумент комплексной проводимости цепи φ равен нулю, т. е. ψ_i = ψ_u полная проводимость цепи Y = G и общий ток I_рез = GU минимальный.

Режим участка цепи с параллельными ветвями, при котором сдвиг фаз между напряжением на его выводах и общим током равен нулю, называется резонансом токов.

При резонансе действующие значения токов в индуктивном и ем­костном элементах одинаковые: I_L = (1/ω_рсзL)U = 1_С = ω_резСU, а сдвиг фаз между токами равен π, так как ток в индуктивном элементе отстает от напряжения по фазе на угол π/2, а ток в емкостном элементе опережает напряжение на такой же угол π/2 (рис. 3.17).

Если при резонансе токов в одинаковое число раз п увеличить индуктивную и емкостную проводимости, т. е. заменить B_L = l/ω_резL и В_с = ω_резС на B'_L = nB_L и B'_c= пВ_с, то токи I_L и 1_С увеличатся тоже в п раз, а общий ток останется тем же: I_рез= GU. Таким образом, в принципе можно неограниченно увеличивать токи в индуктивном и емкостном элементах при неизменном токе источника.

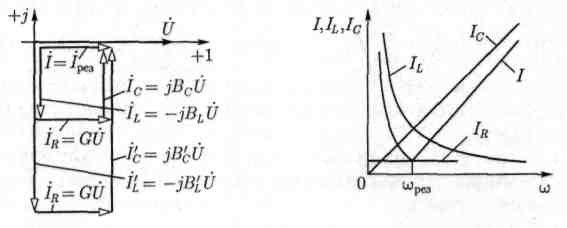
Рис. 3.17 Рис. 3.18

На рис. 3.18 показаны резонансные кривые параллельного контура. В емкостном элементе ток I_c = ωCU возрастает пропорционально угловой частоте, в индуктивном элементе ток I_L = U/(ωL) обратно пропорционален угловой частоте, в резистивном элементе ток I_R = U/R от угловой частоты не зависит. Точка пересечения кривых I_C(ω) и I_L(ω) соответствует резонансу токов, при котором I = I_R = I_рез .

Если проводимость G резистивного элемента равна нулю, то и полная проводимость Y резистивного элемента равна нулю. При этом общий ток цепи (ток источника) также равен нулю, что эквивалентно размыканию цепи.

Последовательно с индуктивным элементом L может быть включен резистивный элемент R_L, а последовательно с емкостным элементом С— резистивный элемент R_C, учитывающие, например, потери энергии в проводах. Условием резонанса токов в такой цепи будет равенство индуктивной и емкостной проводимостей этих ветвей определится:

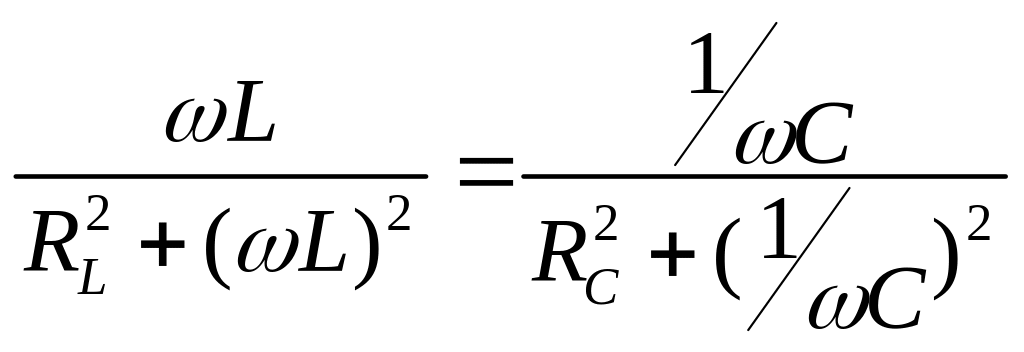
И в этом случае при резонансе общий ток совпадает по фазе с напряжением.

Отметим, что резонанс токов в отличие от резонанса напряжений — явление безопасное для электроэнергетических установок. Резонанс токов, как и резонанс напряжений, находит применение в радиотехнических устройствах.

3.10. Цепи с индуктивно связанными элементами

У двух катушек индуктивности с числами витков w₁ и w₂ и токами i₁ и i₂ (рис. 3.19,а), достаточно близко расположенных относительно друг друга, часть магнитных линий поля каждой из катушек может быть сцеплена с витками другой катушки. Поэтому кроме собственных потокосцеплений каждой из катушек ψ₁₁ и ψ₂₂ нужно при расчетах таких цепей учитывать добавочные потокосцепления витков первой 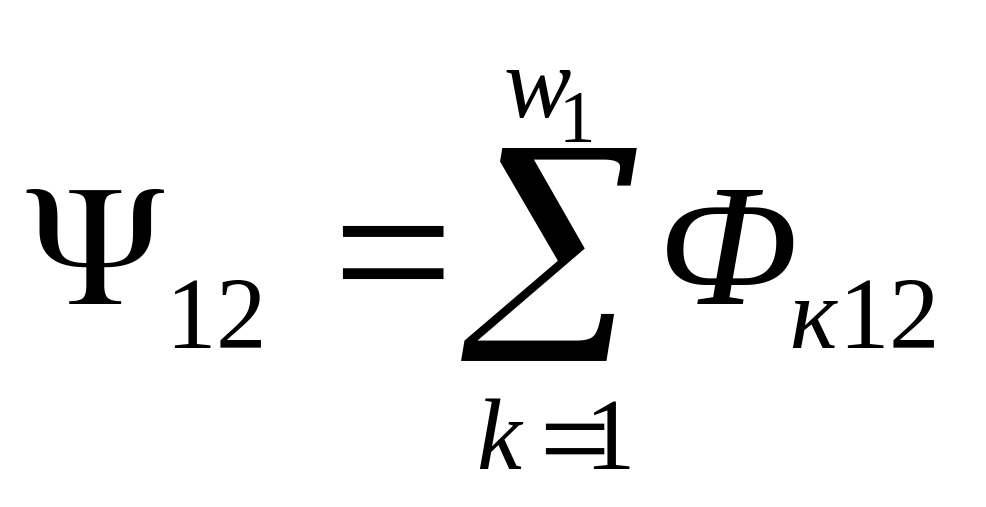и второй 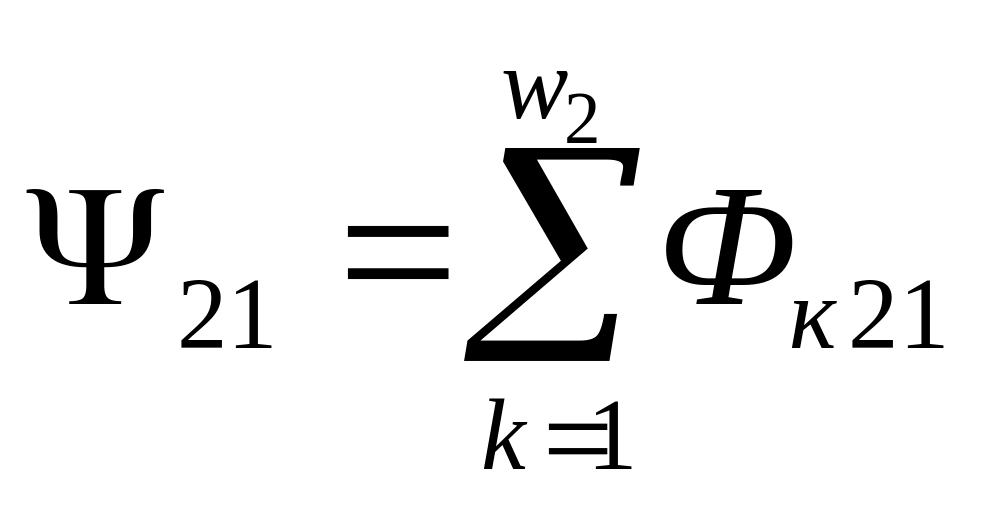катушек, где Ф_к12 — поток через к-й виток первой катушки от тока во второй катушке, а Ф_к21 — поток через к-й виток второй катушки от тока в первой катушке.

Отношение добавочного потокосцепления первой катушки Ψ₁₂ к току i₂ второй катушки называется взаимной индуктивностью первой и второй катушек:

М₁₂ = Ψ₁₂/i₂.

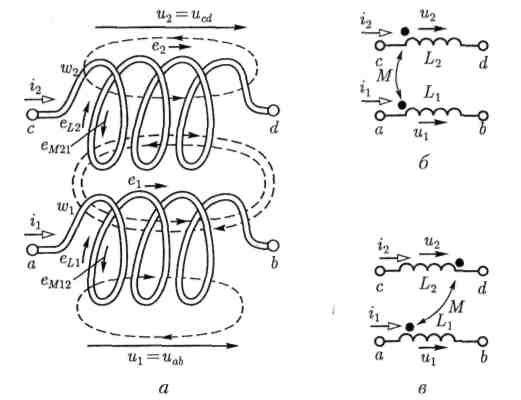
Рис. 3.19

Аналогично определяется взаимная индуктивность второй и первой катушек:

М₂₁ = Ψ₂₁/i₁.

Опыт показывает, что М₂₁ = М₁₂ = М. Строгое доказательство этого условия возможно с применением теории электромагнитного поля. Взаимная индуктивность в линейных цепях не зависит от направлений и значений токов, а определяется только конструкцией катушек и их взаимным расположением.

Полное потокосцепление Ψ каждой из двух рассматриваемых ин­дуктивно связанных катушек содержит две составляющие, которые могут складываться или вычитаться в зависимости от направления токов в катушках и их взаимного расположения. В первом случае включение индуктивно связанных катушек называется согласным, во втором случае — встречным. Так как эскизное изображение индуктивно связанных катушек сложно

(рис. 3.19,а), то для описания характера индуктивной связи пользуются условными обозначениями.

На схемах замещения цепей обозначают точками (рис. 3.19,б и в) одноименные выводы («начала») каждой из катушек. Если токи направлены одинаково относительно одноименных выводов (рис. 3.19,б), то катушки включены согласно. Собственное и добавочное потокосцепления в каждой катушке должны суммироваться, т.е. полное потокосцепление первой катушки

Ψ₁ = Ψ₁₁ + Ψ₁₂

и полное потокосцепление второй катушки

Ψ₂ = Ψ₂₂ + Ψ₂₁.

Если токи направлены по-разному относительно одноименных выводов (рис. 3.19, в), то катушки включены встречно, т.е.

Ψ₁ = Ψ₁₁ - Ψ₁₂; Ψ₂ = Ψ₂₂ - Ψ₂₁

Здесь, как и ранее, под направлениями токов следует понимать их выбранные положительные направления.

Согласно закону электромагнитной индукции в каждой катушке будет индуктироваться ЭДС. В первой катушке ЭДС индукции

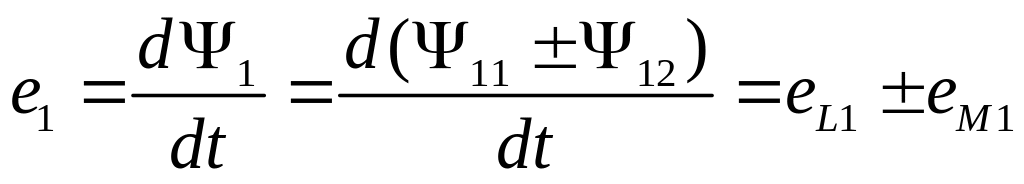(3.16,а)

и во второй катушке

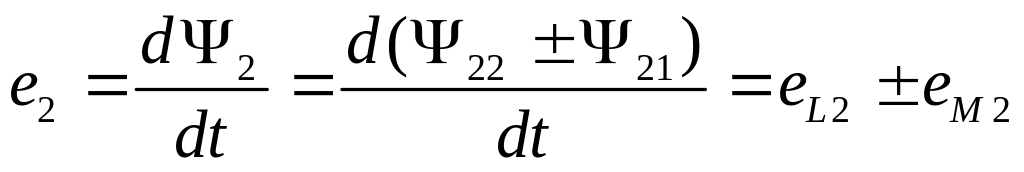(3.16,б)

где e_L1 = — dΨ₁₁/dt = —L₁di/dt, e_L2 = — dΨ₂₂/dt = —L₂di₂/dt — ЭДС самоиндукции первой и второй катушек; е_М1 = — dΨ_l2/dt = —Mdi₂/dt;

e_M2 = - dΨ₂₁/dt = —Mdi₁/dt — ЭДС взаимной индукции первой и второй катушек.

На рис. 3.19,а показано, что внутри катушек собственный магнитный поток и магнитный поток, вызванный током в другой катушке, направлены встречно, что соответствует нижнему знаку в (3.16) и рис. 3.19,в.

Лекция 8