1.2. Программное оптимальное управление и задача стабилизации
Рассмотрим
движение динамической системы (1.1). Пусть
для этой системы найдено оптимальное
управление
и получена соответствующая оптимальная
траектория
.
При реализации оптимальной траектории
в технических задачах неизбежно
наталкиваются на существенные трудности,
заключающиеся в невозможности, во-первых,
точно установить реальную систему (или
объект управления) в начальное состояние
,
во-вторых, точно реализовать само
оптимальное управление
,
в третьих, точно предсказать заранее
внешние условия функционирования
системы (приближенность исходной
математической модели). Все это приводит
к необходимости решать задачу о коррекции
закона оптимального управления в
процессе функционирования любой
технической системы (или объекта). Таким
образом, задачу оптимального управления
в реальных условиях можно разделить на
две части: 1) построение номинального
оптимального управления
исходной динамической системой в
идеальных условиях в рамках математической
модели (1.1); 2) построение корректирующих
управляющих воздействий
с целью реализации заданного номинального
оптимального управления
и оптимальной траектории
в процессе функционирования системы.
Первую часть задачи оптимального
управления принято называть задачей
построения оптимального программного
управления [3], причем она решается в
рамках априорной информации, известной
заранее о рассматриваемой системе.
Вторую часть задачи называют задачей
стабилизации заданной номинальной
программы управления [3] и решаться она
должна в процессе функционирования
системы по информации, поступающей от
измерительных устройств системы
управления. Задача стабилизации
номинальной программы управления тоже
может быть поставлена как задача поиска
оптимального управления
по соответствующему критерию, что будет
сделано ниже (см. раздел 1.4).
Замечание.
Очевидно, что в качестве номинальной
программы управления может быть
использована не только оптимальное
управление
,
но и любое другое допустимое управление
(если задача оптимизации программного
управления не решается). В частном самом
простом случае может быть, например,
поставлена задача о стабилизации
некоторого постоянного положения
системы
.
1.3. Невозмущенное и возмущенное движения динамической системы
Так как реальное движение системы неизбежно отличается от номинального программного, то этот факт привел к концепции невозмущенного и возмущенного движений Ляпунова А.А. [4]. Так, любое программное движение системы (1.1), независимо от того является ли оно оптимальным или допустимым называется невозмущенным движением. Причем этому движению соответствует некоторое частное решение системы (1.1). Возмущенное движение оценивается при этом некоторыми отклонениями от невозмущенного движения. Следовательно, возмущенное движение будет описываться следующими переменными
,
,
(1.3)
где
переменные
и
характеризуют номинальную программу
управления, а переменные
и
- отклонения от номинальной программы.
Подставляя соотношения (1.3) в систему (1.1), получим
.
(1.4)
Прибавляя
и отнимая в правой части системы (1.4)
одинаковое слагаемое
и учитывая, что
,
(1.5)
получим систему в отклонениях от номинального движения
,
(1.6)
где
,
,
а
определяются в результате решения
системы (1.5).
Обычно
считают, что отклонения
и
от номинального движения являются
малыми величинами. Поэтому, если разложить
функцию
в ряд Тейлора и ввести обозначения
,
,
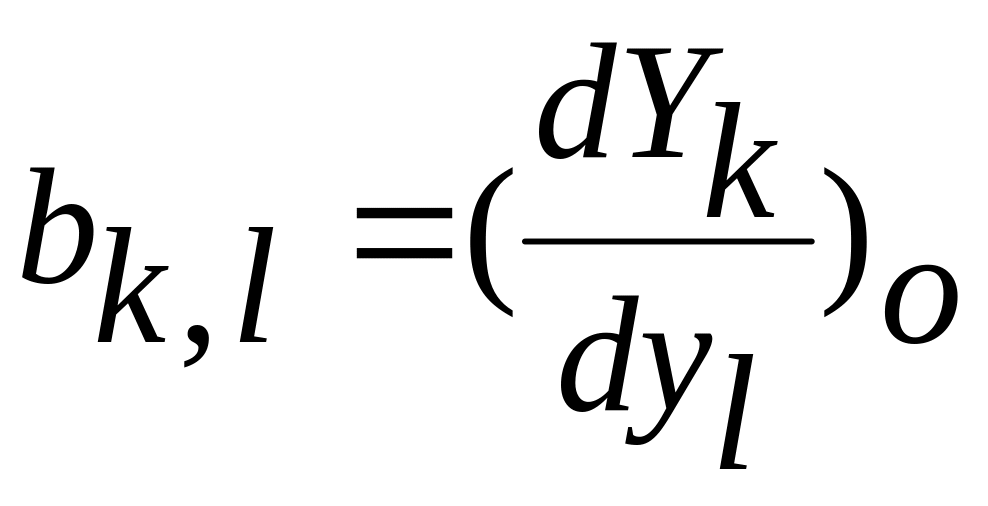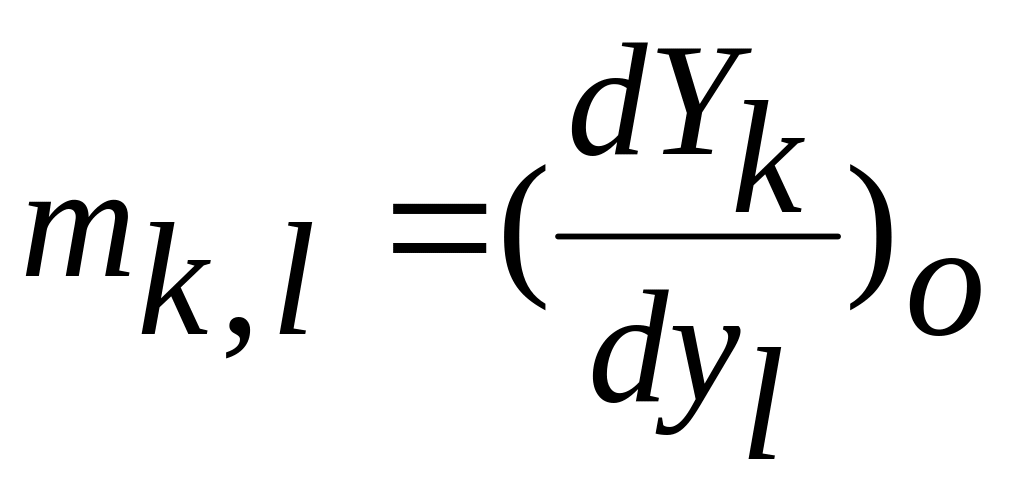где индекс (o)
означает, что частные производные
определяются для заданной номинальной
программы, то получим
.
(1.7)
Здесь
функция
определяет слагаемые второго порядка
и выше по отклонениям
;
матрицы
и
выделяют линейную часть ряда и имеют
компоненты
и
;
.
Уравнения,
записанные в отклонениях (1.7), имеют
большое значение в теории управления.
На основании этих уравнений производится
постановка большого количества задач
оптимизации, имеющих практический
интерес. Одна из этих задач – задача
стабилизации, сформулированная выше.
При решении этой задачи требуется
определить, как следует выбрать
корректирующие управляющие воздействия
,
чтобы уменьшить отклонения
в некотором смысле наилучшем образом.