4.4. Пример оптимального выбора коэффициентов регулятора при управлении линейной системой второго порядка

Пусть уравнения объекта управления имеют вид

, , (4.22)

где , - переменные состояния системы, , , , , , - заданные параметры системы, - скалярное управление.

Необходимо для системы (4.22) решить задачу стабилизации, то есть найти управление , переводящее систему из некоторого начального состояния , в начало координат , где - заданное время. При этом критерий оптимальности

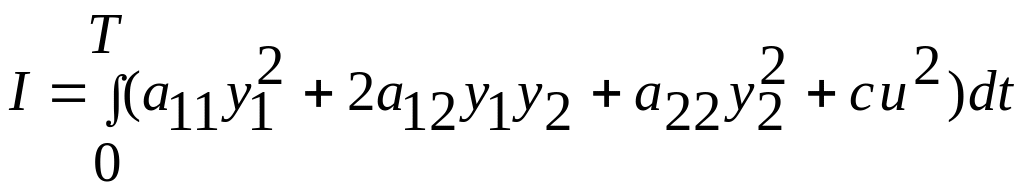, (4.23)

должен быть минимальным. Коэффициенты , , , считаются заданными, а функция, стоящая под знаком интеграла (4.23), является определенно положительной.

Задача оптимального управления решается в классической постановке без задания дополнительных ограничений. Решение поставленной задачи как показано выше (см. раздел 4.1) сводится к решению системы алгебраических уравнений (4.4), из которой находятся параметры , , , определяющие коэффициенты , оптимального регулятора (4.7) и, следовательно, оптимальное управление (4.6).

Для системы второго порядка (4.22) и критерия (4.23) система алгебраических уравнений (4.4) примет вид

,

, (4.24)

.

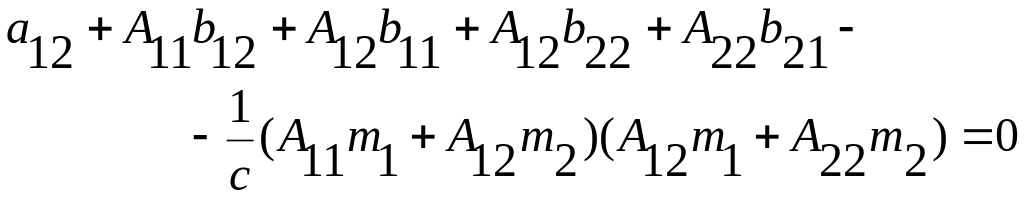Система алгебраических уравнений (4.24) может быть решена каким-либо численным методом и может иметь несколько решений. Из всех возможных решений необходимо выбрать такое, которое удовлетворяет условиям Сильвестра

, , (4.25)

обеспечивающим положительную определенность функции Ляпунова как квадратичной формы (4.1). Тогда оптимальное управление будет иметь вид

. (4.26)

Здесь

,

коэффициенты оптимального регулятора (стабилизатора).

Пример.

Рассмотрим некоторый объект управления, поведение которого описывается системой обыкновенных дифференциальных уравнений второго порядка (4.22) с матрицей и вектором вида

, ,

и критерием оптимальности (4.23) с параметрами , , , . Данный пример был решен в математическом пакете Mathcad. При решении подобных задач рекомендуется придерживаться следующего плана:

1. Определение управляемости линейной системы.

2. Построение фазового портрета исходной системы без управления .

3. Определение оптимального управления с помощью принципа динамического программирования Беллмана.

4. Построение фазового портрета полученной системы с выбранном управлением.

Определение управляемости линейной системы производится по методике, изложенной в разделе 2.2. На этом этапе решаются следующие задачи: а) определение собственных значений матрицы ; б) определение собственных векторов матрицы ; в) приведение исходной системы к главным координатам с помощью матрицы преобразования , составленной из собственных векторов матрицы . Управляемость линейной системы в конечном счете определяется по вектору управления для системы (2.5), записанной в главных координатах. В соответствии с критерием Гильберта линейная система управляема, если ни одна компонента вектора не является нулевой (см. раздел 2.2).

Для рассматриваемого примера решение задачи определения управляемости имеет вид:

собственные значения матрицы

, ;

собственные вектора матрицы

, ;

матрицы и

, ;

вектор

.

Здесь - мнимая единица ( ).

Так как компоненты вектора отличны от нуля, то рассматриваемая система управляема.

Фазовый портрет линейной системы второго порядка это изображение поведения динамической системы на фазовой плоскости в координатах ( ). Фазовый портрет линейной системы полностью определяется ее собственными значениями . Методика построение фазовых портретов линейных систем второго порядка приводится в Приложении 2. В рассматриваемом примере собственные значения исходной системы без управления - комплексно сопряженные числа, причем вещественные части этих чисел положительны. Поэтому фазовый портрет исходной системы соответствует особой точке типа «неустойчивый фокус» и приводится на рис.1. На фазовой плоскости необходимо также получить характерную фазовую траекторию системы с помощью метода численного интегрирования. Эти вычисления также можно провести с помощью программных средств математического пакета Mathcad.

Фазовый портрет исходной линейной системы без управления

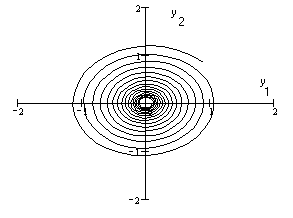
Рис. 4.1

Для определения оптимального управления с помощью принципа Беллмана необходимо решить систему алгебраических уравнений (4.24) относительно параметров . Анализ численных решений этой системы для рассматриваемого примера показывает, что данная система имеет два вещественных решения 1) ; 2) . Первое решение не удовлетворяет условиям Сильвестра (4.25), поэтому оно должно быть отброшено. Второе решение удовлетворяет условиям (4.25) и соответствующая этому решению функция Ляпунова дает решение задачи оптимального управления для рассматриваемой линейной системы. Тогда оптимальное управление принимает вид (4.26)

. (4.27)

Здесь коэффициенты оптимального регулятора и .

Формула (4.27) дает решение задачи оптимального управления в форме синтеза, так как оптимальное управление получено как функция фазовых переменных и это управление определено для любой точки фазовой плоскости .

После определения оптимального управления необходимо подставить функцию в систему (4.22) и привести подобные члены. Приведение несложных преобразований дает

,

(4.28)

.

Полученная система (4.28) в теории автоматического управления называется замкнутой системой, так как в нее уже подставлена функция управления . При этом управление осуществляется следующим образом: в системе производится измерение фазовых переменных и на ее вход подается управление (4.27). Тем самым производится замыкание системы и получается классическая система с обратной связью.

Подставив в систему (4.28) числовые значения параметров, для рассматриваемого примера получим

,

. (4.29)

Фазовый портрет замкнутой линейной системы (4.29) также определяется ее собственными числами: , значения которых соответствуют особой точке типа «устойчивый фокус» (см. Приложение 2). Линейная замкнутая система получается асимптотически устойчивой, так как с течением времени фазовая точка стремится к началу координат при . При этом функции совершают колебания относительно оси времени .

Фазовый портрет замкнутой линейной системы с управлением

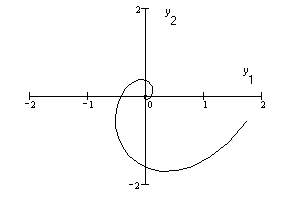
Рис.4.2