Вопрос 19 Понятие непрерывности функции

Пусть функция определена в точке и любая -окрестность точки содержит отличные от точки области задания этой функции.

Определение. Функция называется непрерывной в точке , если предельное значение этой функции в точке существует и равно частному значению , то есть, если

. (1)

Поскольку , то равенство (1) можно представить в виде

.

Следовательно, для непрерывной функции знак предела можно вносить под знак функции.

Определение. Функция называется непрерывной справа (слева) в точке , если правое (левое) предельное значение этой функции в точке существует и равно частному значению .

Заметим, что если правое и левое предельные значения в точке существуют и

,

то предельное значение в точке также существует и равно . Следовательно, если функция непрерывна в точке справа и слева, то она непрерывна в этой точке.

Определение. Точки, в которых функция не является непрерывной называются точками разрыва функции.

Определение. Функция называется непрерывной на множестве , если она непрерывна в каждой точке этого множества.

Ранее мы доказали, что для любого вещественного числа , , , , где — алгебраический многочлен порядка . Следовательно, функции , , , являются непрерывными на всей числовой оси. Функция имеет разрыв в точке , так как она не определена в данной точке.

Вопрос 20 Арифметические операции над непрерывными функциями

Теорема. Пусть заданные на одном и том же множестве функции и непрерывны в точке . Тогда функции , , и также непрерывны в точке (частное при условии ).

Доказательство. Поскольку и непрерывны в точке , то и . Используя теорему об арифметических операциях над функциями, имеющими конечные предельные значения, получим:

,

,

.

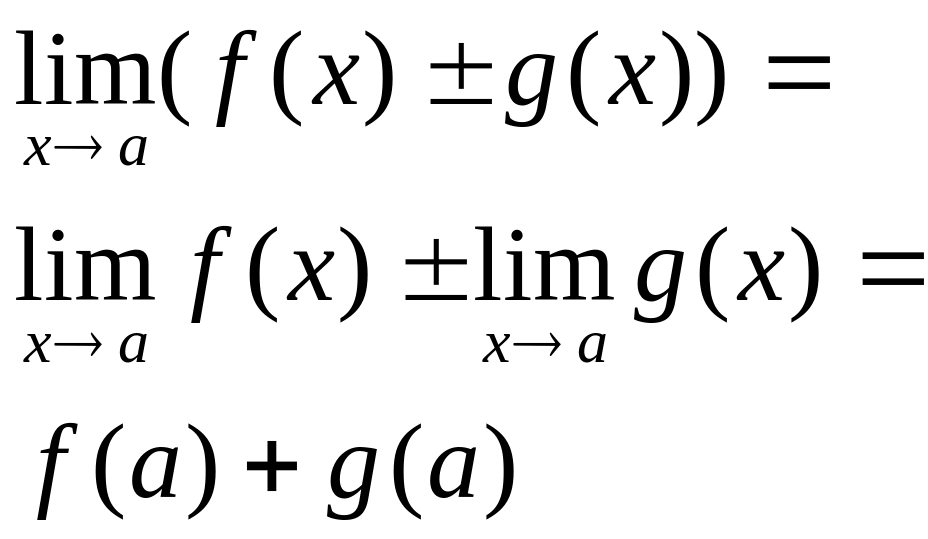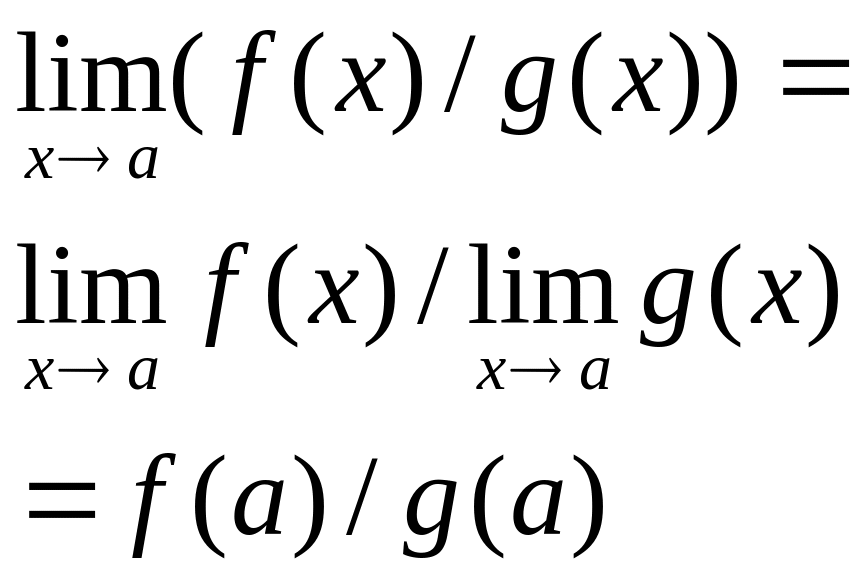Следовательно, функции , , и непрерывны в точке (частное при условии ).

Вопрос 21 Сложная функция и ее непрерывность

Последовательное применение двух или нескольких функций называется суперпозицией этих функций.

Функции, образованные в результате суперпозиции двух или нескольких функций будем называть сложными функциями. Например, сложная функция образована в результате суперпозиции функций и .

Достаточно определить сложную функцию, образованную в результате суперпозиции двух функций. Пусть функция определена на некотором множестве и пусть — множество значений этой функции. Если на указанном множестве определена другая функция , то говорят, что на множестве задана сложная функция переменной

.

Теорема. Если функция непрерывна в точке , а функция непрерывна в точке , соответствующей точке , то функция непрерывна в точке .

Вопрос 22 Классификация точек разрыва

Устранимый разрыв. Точка называется точкой устранимого разрыва функции , если предельное значение функции в этой точке существует, но либо функция не определена в этой точке, либо ее предельное значение не равно частному значению .

Если функция имеет в точке разрыв такого рада, то его можно устранить, определив значение функции в точке равным ее предельному значению в этой точке. Например, функция не определена в точке , но имеет в этой точке предельное значение, равное 1. Следовательно, точка является точкой устранимого разрыва. Если положить значение функции в нуле равным 1, то получим непрерывную функцию

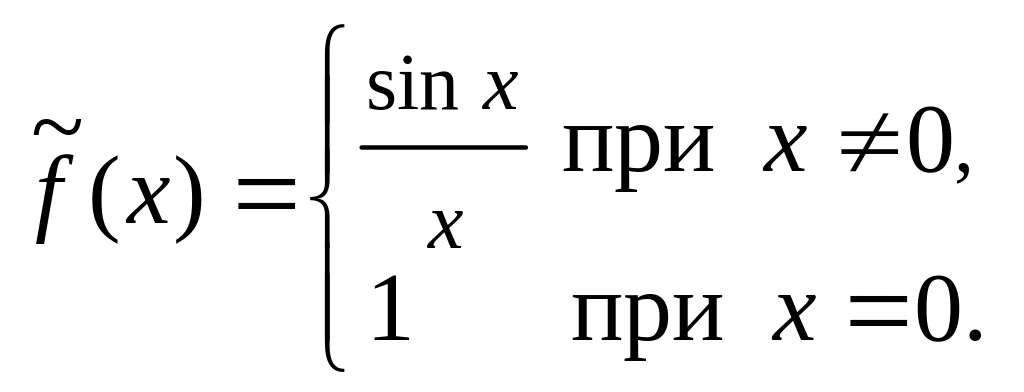
Разрыв первого рода. Точка называется точкой разрыва первого рода, если в этой точке функция имеет конечные, но не равные друг другу правое и левое предельные значения:

.

Например, для функции точка является точкой разрыва первого рода. Действительно, , а .

Разрыв второго рода. Точка называется точкой разрыва второго рода, если в этой точке функция не имеет хотя бы одного одностороннего предельные значения, или если по крайней мере одно из односторонних предельных значений бесконечно.

Ранее мы показали, что функция не имеет предельного значения в точке . Следовательно, точка является для данной функции точкой разрыва второго рода.

Функция также имеет в точке разрыв второго рода, поскольку .

Определение. Функция называется кусочно непрерывной на отрезке , если она непрерывна во всех внутренних точках этого отрезка, за исключением, может быть, конечного числа точек, в которых имеет разрыв первого рода, и, кроме того, имеет односторонние предельные значения в точках и .